Некоторые экономические задачи, приводящие

МАТЕМАТИЧЕСКИЕ МЕТОДЫ ЛИНЕЙНОЙ ОПТИМИЗАЦИИ

Начало линейной оптимизации было положено в 1939 г., когда вышла в свет работа профессора Ленинградского университета Л.В. Канторовича «Математические методы организации и планирования производства». Академик Л.В. Канторович за разработку методов решения оптимизационных задач был удостоен звания лауреата Ленинской премии в 1964 г. и Нобелевской премии по экономикек в 1975 г.

Линейная оптимизация (линейное программирование) – это разде математического программирования, включающий в себя теорию и методы решения практических задач, в которых критерий оптимальности линейно зависит от параметров задачи, а ограничениями являются линейные уравнения и неравенства.

к задачам линейного программирования

1) Задача использования сырья

Для изготовления двух видов продукци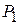и и 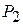используют 3 вида сырья . Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также величина прибыли, получаемой от реализации продукции, приведены в таблице 3.1.

Необходимо составить такой план выпуска продукции, чтобы при её реализации получить максимальную прибыль.

Таблица 2.1. Таблица показателей для задачи использования сырья

Вид сырья	Запас сырья	Количество единиц сырья, идущих на изготовление единицы продукции
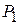
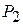
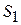
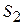
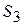
Прибыль от единицы продукции, руб.

Пусть 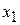- количество единиц продукции 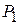, 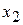- количество единиц продукции 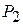. Тогда учитывая количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также запасы сырья, получим систему ограничений:

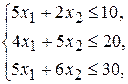(2.1)

которая показывает, что количество сырья, расходуемого на изготовление продукции, не может быть больше имеющихся запасов.

Если 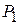не выпускается, то 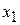=0, в противном случае 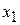>0. Аналогично, если 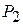не выпускается, то 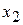=0, в противном случае 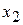>0, т.е.

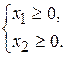(2.2)

Реализация 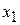единиц продукци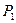и и 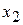единиц продукции 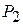дает соответственно 30 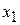и 45 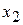руб. прибыли. Суммарная прибыль:

.

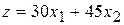Необходимо найти такие 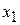и 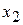, при которых функция z достигает максимума.

z называется целевой функцией и вместе с системой ограничений (2.1) и (2.2) образует математическую модель экономической задачи.

Задачу можно легко обобщить (таблица 2.2).

Таблица 2.2. Таблица показателей для задачи использования сырья

Вид сырья	Запасы сырья	Количество единиц i-го сырья, идущего на изготовление единицы j-ой продукции
			…
					…
					…
…	…	…	…	…	…	…
					…
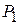
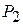
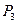
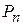
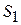
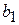
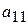
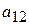
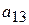
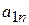
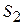
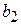
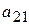
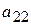
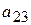
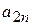
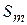
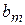
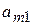
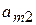
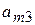
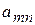
Прибыль				…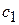

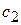
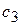
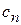
Пусть при выпуске n видов продукции используется m видов сырья. Обозначим через 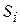виды сырья (i= 1,2,…, m); 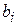- запасы сырья i -го вида; 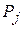- виды продукции (j= 1,2,…, n); 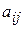- количество единиц i- го сырья, идущего на изготовление единицы j- ой продукции; 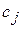- величину прибыли, получаемой при реализации единицы j- ой продукции.

Пусть 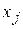- количество единиц j- ой продукции, которое необходимо произвести.

Целевая функция .

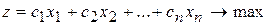Система ограничений:

,

.

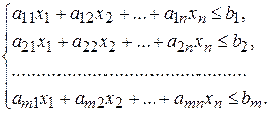
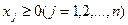2) Задача составления рациона

При откорме каждое животное должно ежедневно получить не менее 8 единиц питательного вещества 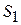, не менее 6 единиц вещества 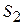и не менее 10 единиц вещества 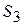. Для составления рациона используют 2 вида корма. Содержание количества единиц питательных веществ в 1 кг каждого вида корма и стоимость 1 кг корма приведены в таблице:

Таблица 2.3. Таблица показателей для задачи составления рациона

Питательные вещества	Количество единиц питательных веществ в 1 кг корма
Корм 1	Корм 2
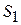
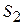
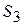
Стоимость 1 кг корма, руб.

Необходимо составить дневной рацион нужной питательности, причем затраты на него должны быть минимальными.

Пусть 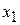- количество килограмм корма 1, 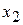- количество килограмм корма 2 в дневном рационе.

Т.к. дневной рацион удовлетворяет требуемой питательности только в том случае, если количество единиц питательных веществ не меньше предусмотренного, получаем систему ограничений:

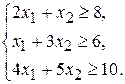(2.3)

Если корм 1 не используется, то 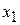=0, в противном случае 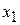>0. Аналогично, если корм 2 не выпускается, то 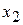=0, в противном случае 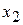>0, т.е.

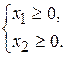(2.4)

Необходимо добиться минимальных затрат на дневной рацион, т.е.

.

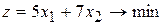Задачу можно обобщить, если предусмотреть в рационе m видов питательных веществ в количестве не менее 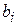(i= 1,2,…, m) единиц и использовать n видов кормов.

Для составления математической модели задачи обозначим 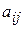(j= 1,2,…, n) - количество единиц i- го питательного вещества, содержащегося в единице j- го корма; 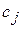- стоимость единицы j- го корма.

Пусть 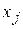- количество единиц j- го корма в дневном рационе.

Необходимо найти минимальное значение линейной функции

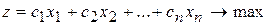
при ограничениях

, .

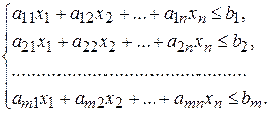
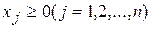Дата добавления: 2015-05-26