Поиск оптимального решения

Структура рабочего листа

Решение оптимизационной задачи

3.4.1. Задача на оптимальное распределение ресурсов

Пример 3.2. Работу с надстройкой Поиск решения рассмотрим на примере 2.4, приведенном в пункте 2.4.2:

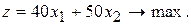
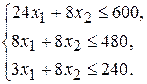
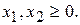
Занесем матрицу коэффициентов перед неизвестными в ячейки А2:В4, а столбец свободных членов в ячейки Е2:Е4. Ячейки С2:С3 оставим пустыми, т.к. это ячейки, которые могут изменяться в процессе поиска решения (в них у нас будут неизвестные системы 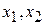). В ячейках D2:D4 запишем формулы для левых частей неравенств системы ограничений, а в ячейку C6 запишем формулу для целевой функции z (рис. 3.2).

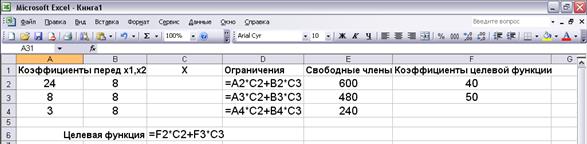
Рис. 3.2. Структура рабочего листа

Чтобы найти наилучшее решение:

1. Выделите оптимизируемую ячейку. В примере 3.2 ячейка С6.

2. Выберите команду Сервис, Поиск решения. При этом появится незаполненное диалоговое окно Поиск решения (рис. 3.3.).

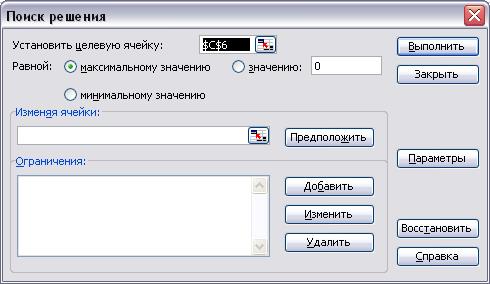
Рис. 3.3. Диалоговое окно Поиск решения.

3.В поле Установить целевую ячейку уже находится ссылка на выделенную на первом шаге ячейку. При необходимости эту ссылку можно изменить.

4.Установите тип взаимосвязи между целевой ячейкой и решением путем выбора переключателя в группе Равной. Назначение этих переключателей описано в таблица 3.1. В данном случае нам требуется найти максимальное значение целевой ячейки.

Таблица 3.1. Назначение переключателей в группе Равной

Переключатель	Описание
Максимальному значению	Поиск максимального значения для целевой ячейки
Минимальному значению	Поиск минимального значения для целевой ячейки
Значению	Поиск заданного (фиксированного, рассчитываемого по формуле целевой ячейки) значения для целевой ячейки

5. В поле Изменяя ячейки укажите ячейки-параметры, которые могут изменяться в процессе поиска решения. В данном примере это ячейки С2:С3.

Замечание. В некоторых случаях можно воспользоваться возможностью автоматического поиска ячеек-параметров. Для этого необходимо нажать кнопку Предположить. При этом в поле Изменяя ячейки попадут все ячейки, не содержащие формулы и влияющие на формулу, ссылка на которую дана в поле Установить целевую ячейку.

6. Нажмите кнопку Добавить, чтобы ввести ограничения задачи. При этом откроется диалоговое окно Добавление ограничения (рис. 3.4).

7. Введите первое ограничение. В данном примере значение в ячейке D2 не должно превышать значения в ячейке Е2.

В поле Ссылка на ячейку укажите ячейку D2, а в поле Ограничение укажите ячейку Е2. Знак отношения <=, установленный по умолчанию, в данном случае можно не изменять (рис 3.4.).

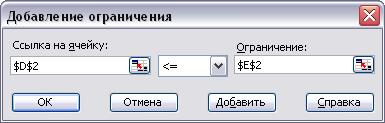
Рис. 3.4. Заполненное диалоговое окно Добавление ограничения

Замечание. Если требуется указать более одного ограничения, прямо в этом же окне следует нажать кнопку Добавить. При этом текущее ограничение будет добавлено в список ограничений задачи, а поля окна будут очищены для указания следующего ограничения. Для завершения ввода нескольких ограничений следует нажать кнопку ОК, когда в полях указано последнее из вводимых ограничений.

8. Нажмите кнопку ОК. В результате появится заполненное диалоговое окно Поиск решения (рис. 3.5).

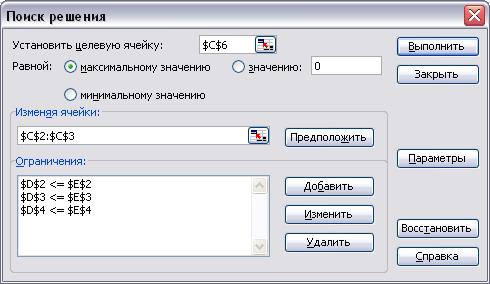
Рис. 3.5. Заполненное диалоговое окно Поиск решения

9. Нажмите кнопку Параметры. В результате появится диалоговое окно Параметры поиска решения. Установите флажок напротив параметров линейная модель и Неотрицательные значения (рис. 3.6). Нажмите ОК.

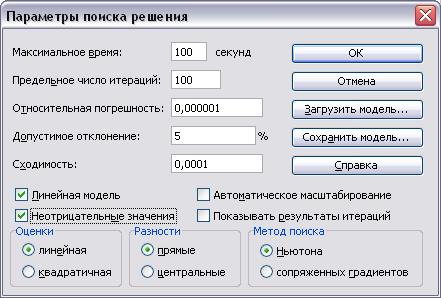
Рис. 3.6. Диалоговое окно Параметры поиска решения

10. Нажмите кнопку Выполнить. По окончании поиска решения появится диалоговое окно Результаты поиска решения (рис. 3.7).

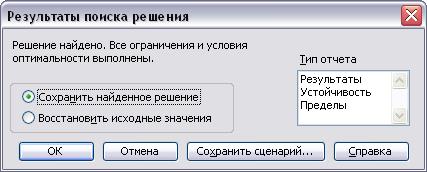
Рис. 3.7. Диалоговое окно Результаты поиска решения

11. Выберите переключатель Сохранить найденное значение, чтобы сохранить найденные значения, или переключатель Восстановить исходные значения, чтобы оставить значения, которые были на рабочем листе. С помощью этого диалогового окна можно сформировать отчет.

12. Нажмите кнопку ОК.

Решение, найденное с помощью средства Поиск решения следующее (рис. 3.8):

z= 1864,286; 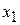=17,14286; 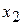=23,57143.

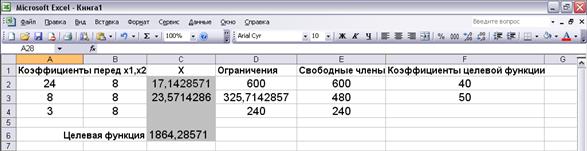
Рис. 3.8. Оптимальное решение

Такое же решение нами было найдено графически в пункте 2.4.2.

После нажатия кнопки ОК в окне Результаты поиска решения (рис. 3.7) параметры модели автоматически сохраняются в именованных формулах на рабочем листе (и соответственно модель может быть сохранена в этом файле). Чтобы позднее запустить процесс поиска решения с другими ограничениям необходимо открыть диалоговое окно Поиск решения (командой Сервис, Поиск решения и отредактировать необходимые неравенства.

После того как решение найдено, можно сохранить ссылки на изменяемые ячейки, чтобы использовать их в составе сценария. Для этого нужно нажать кнопку Сохранить сценарий в диалоговом окне Результат поиска решения. В предъявленном диалоговом окне (рис. 3.9) необходимо ввести имя сценария и нажать кнопку ОК.

Рис. 3.9. Диалоговое окно Сохранение сценария

Под этим именем (которое должно быть уникальным для сценариев текущей рабочего листа) будут сохранены исходные значения, содержащиеся в изменяемых ячейках. Таким способом можно сохранить несколько вариантов решения, а затем с помощью диспетчера сценариев просмотреть и сравнить их.

Можно сохранить параметры, но не запускать процесс поиска решения. Для этого в диалоговом окне Поиск решения введите, как описано выше, новые необходимые величины и условия, а затем нажмите кнопку Закрыть.

Изменение ограничений

Поиск решения позволяет экспериментировать с различными параметрами задачи для определения наилучшего варианта решения. При этом, изменив ограничения, можно оценить изменение результата.

Оценим, как отразится изменение ограничения сырьевых ресурсов с 600 на 500, с 480 на 450, с 240 на 200 на размере общей прибыли. Запишем новые объемы сырьевых ресурсов в ячейках G2, G3, G4.

Для этого выполните следующие действия:

− выберите команду Сервис, Поиск решения;

− в диалоговом окне Поиск решения в списке имеющихся ограничений Ограничения выделите нужное ограничение и нажмите кнопку Изменить;

− в предъявленном диалоговом окне Изменение ограничения измените условия ограничения (в данном случае замените ячейку E2 на G2, E3 на G3, E4 на G4) и нажмите кнопку ОК;

− нажмите кнопку Выполнить;

− в предъявленном окне Результаты поиска решения (рис. 3.7) выберите переключатель Сохранить найденное значение и нажмите кнопку ОК.

Сумма прибыли при новом ограничении уменьшилась с 1864,286 до 1553,571 млн. руб. Изменились и значения переменных (рис. 3.10).

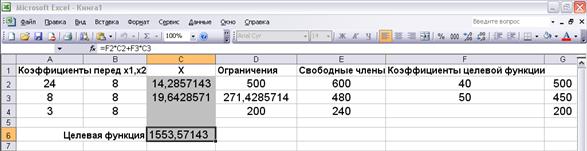
Рис. 3.10. Решение задачи с новыми ограничениями

Ограничения можно удалить. Для этого в диалоговом окне Поиск решения выделите ненужное неравенство и нажмите кнопку Удалить. Чтобы сбросить все параметры в диалоговом окне Поиск решения нажмите кнопку Восстановить.

Виды ограничений

Помимо ограничений, представимых в виде равенств и неравенств (с помощью знаков >=, <= и =), можно использовать условие целочисленности.

По результатам последнего поиска решений в ячейке С2 содержится число 14,28571. Однако если выделить эту ячейку, то в строке формул будет выведена величина 14,2857142857143. Эта величина округляется при выводе на экран, однако при вычислении результата используются неокругленные значения. Аналогично нецелые числа с большим количеством знаков после запятой содержатся в ячейке С3.

Очевидно, что очень часто при решении оптимизационных задач изменяемые данные должны быть целочисленными (суммы должны быть, например, округлены до целых денежных единиц, количества штучных ресурсов должны быть целыми числами).

Чтобы в расчетах участвовали целочисленные значения, выберите команду Сервис, Шнек решения, введите условие целочисленности и запустите поиск снова. Чтобы добавить условие целочисленности для объемов производства:

− В диалоговом окне Поиск решения нажмите кнопку Добавить.

− В поле Ссылка на ячейку укажите ячейки $С$2: $С$3.

− Выберите цел в качестве операции сравнения(рис. 3.11).

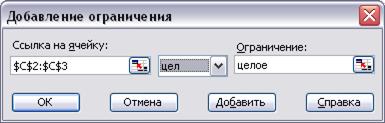
Рис. 3.11. Добавление условия целочисленности

− Нажмите кнопку ОК. Врезультате в списке Ограничения диалогового окна Поиск решения появится строчка $С$2:$С$3=целое.

− Нажмите кнопку Выполнить. Начнется поиск решения (из-за условия целочисленности процесс поиска может заметно замедлиться).

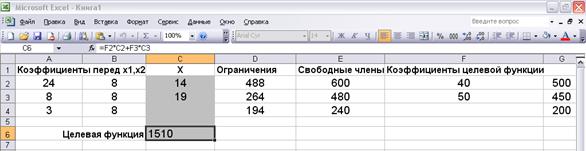
Рис. 3.12. Целочисленное решение

Полученные результаты действительно целые, причем это не просто округленные значения предыдущего решения (рис.3.12).

Дата добавления: 2015-05-26