Одинаковое отображаем одинаково, разное - по-разному

Эстетики и логика

Логико-графические схемы могут быть очень красивыми и не очень... Но если вопрос касается не изобразительного искусства, а логико-графического структурирования, то хорошая фигура для нас — это не формальное соблюдение пропорций и художественное оформление пространства схемы, а легкость выделения нужных для понимания соотношения понятий гештальтов. То есть они должны быть сразу увидены, усмотрены. И в дальнейшем не потеряны. Это в основном и должно нас заботить в схеме, а не формальное соответствие канонам красоты. Красота важна, но не в ущерб понятности смысла.

Многие авторы схем стремятся к симметрии, считая ее более красивой. Но для понимания материала лучше, если в схеме есть элемент асимметрии. Это лучше для запоминания. Потому что запоминается легче что-то отличное от другого.

Один из моментов, составляющих красоту схемы, ее компактность. Компактными или некомпактными могут быть фигуры-понятия. Компактными или некомпактными могут быть хитросплетения связующих фигуры-понятия линий. И компактной или некомпактной может быть вся схема. Компактность — не только элемент красоты, она служит и экономии места. При прочих равных условиях лучше, чтобы схема была компактной. Но утрамбовывать материал до такой степени, чтобы разрушились нужные гештальты, не стоит. Тут компактность — ценность третьестепенная. Нам надо экономить время для восприятия, а не место и заботиться о понятности и «запоминаемости» материала.

В практике схематизации часто разные виды связей между понятиями отображаются одинаково. Например, при помощи стрелок отображают и соотношения частей и целого (см. рис. 37) и причинно-следственную зависимость (см. рис. 38).

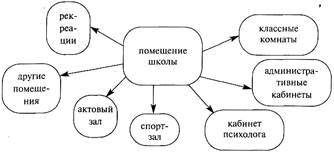
Рис. 37

Рис. 38

Но «части и целое» и «причины и следствия» — это разные виды соотношения понятий.

Или одинаковые по сути соотношения понятий отображаются нередко по-разному. Например, соотношение частей и целого отображается как на рис. 37, но может для этого использоваться и другой способ (см. рис. 39).

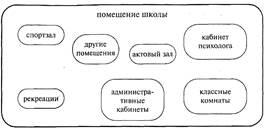
Рис. 39

Конечно, можно одинаковое отобразить по-разному, а разное одинаково, но тогда надо специально это оговорить. Такая свобода вносит путаницу, требует дополнительных временных трат и дополнительных мыслительных усилий, которые более разумно потратить на собственно творчество, а не на распутывание того, что есть что. Из стремления к экономичному результативному мышлению еще раз провозгласим: одинаковое отображаем одинаково, разное — по-разному. Проигрываем в свободе самовыражения, выигрываем во взаимопонимании.

ЧТО ОФОРМЛЯТЬ ЛОГИКО-ГРАФИЧЕСКОЙ СХЕМОЙ?

Соотношения понятий между собой очень многообразны. Если что-либо важно особо осмыслить, запомнить и воспроизвести, то их можно «заструктурировать». Но в науке есть приоритеты. И мы в первую очередь покажем примеры логико-графического структурирования таких соотношений понятий, которые имеют «наибольшее представительство» в научных текстах и которые представляют наибольшую трудность при схематизации. Их и стремятся в первую очередь дать в виде схем сами ученые.

1. КЛАССИФИКАЦИОННОЕ СООТНОШЕНИЕ ПОНЯТИЙ. Это соотношение понятий самое-самое научное. Оно включает родовидовое соотношение, внеположное и перекрестное.

Итак, сначала о родовидовом соотношении. Договоримся отображать родовидовое соотношение понятий так, как ведется со времен Аристотеля (см. рис.40).

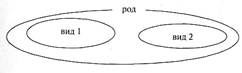
Рис. 40

Примером может быть все, что угодно, ну хотя бы школы, находящиеся рядом, но под разными номерами. (см. рис. 41).

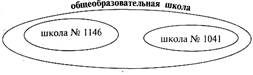
Рис. 41

При этом школа № 1041 и школа № 1146 являются внеположными понятиями, т.е. не включенными одно в другое и неперекрещивающимися. Но поскольку они очень уж близки, рядышком стоят, то можно говорить о рядоположности. Другой простенький пример рядоположных понятий: кошка и собака. А вот в таких «парах»: «вселенная» и «совесть», «собака» и «сено», «кошка» и «компьютер» — понятия слишком далеки друг от друга, они явно внеположные, но и «далекие внеположные». В числе рядоположных в логике выделяются контрарные (противоположные) понятия. Например, добро и зло, холод и тепло, свет и тьма.

В науке, однако, очень часто встречаются «перекрестные» соотношения понятий. Например, «хищная рыба» и «морская рыба». Для ясности: на «перекрестье» расположится, например, акула. Она — хищная морская рыба. А вот хищная неморская (щука, например) расположится в поле левого овала, но вне правого. Нехищная морская — камбала, расположилась в поле правого овала, но вне левого. Заметим, что в духе «одинаковое представлено одинаково, а разное — по-разному» морские рыбы находятся в поле правого овала, хищные — в поле левого, но и те и другие — находятся в одинаковых по размеру овалах (см. рис. 42).

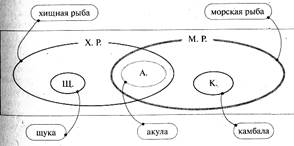Рис. 42

Вглядимся в этот рисунок и констатируем теперь специально, что в нем представлены родовидовые и сопряженные с ними перекрестные соотношения понятий. Так что схемы на этом рисунке можно рассматривать как примеры родовидовых и перекрестных классификационных понятийных хитросплетений.

Обратим внимание, что мы используем те приемы, о которых договорились. Рядоположные видовые понятия отображаем расположенными рядом овальными фигурами. Овальные рамки видовых понятий включены в овальные рамки родовых понятий. Перекрещивающиеся понятия мы отображаем перекрестом их овальных же фигур.

Родовидовые, перекрестные и внеположные соотношения понятий лежат в структуре любой классификации. Попробуем выразить схемой многословный текст: «Четырехугольники делятся на параллелограммы и непараллелограммы. Непараллелограммы делятся на трапеции и четырехугольники неправильной формы. Параллелограммы могут быть прямоугольниками и могут быть ромбами. Прямоугольник может быть квадратом. Некоторые ромбы являются одновременно прямоугольниками. Тогда это квадраты. Квадрат — это и ромб, и прямоугольник, и, конечно же, параллелограмм. Ромб может быть прямоугольником, тогда это квадрат. Непараллелограмм не может быть ромбом или прямоугольником. Конечно же, он не может быть и квадратом». В тексте нет той наглядности, которая делает материал легко понимаемым и легко запоминаемым, что представлено наглядно на приведенной схеме. (Рис. 43).

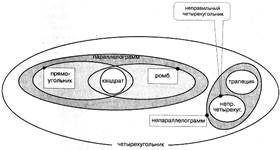
Рис. 43

Но если мы попытаемся выразить в схеме все многообразие соотношений понятий, характерных реальной жизни, то можем прийти к ситуации, примером которой может служить схема из зоологии, созданная по всем ранее оговоренным правилам (см. рис. 44):

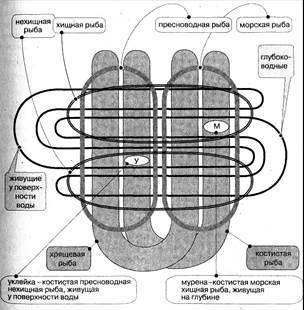
Рис. 44

Остановимся здесь и сделаем очередную мотивирующую и предупреждающую ремарку. Мы поняли, что все «жутко» усложняется. Стоит ли тогда тратить усилия на замену текста логико-графической схемой? Да! Потому что иначе все придется представлять в уме. А ведь и написанные тексты — это попытка вывести «вовне» наши соображения — чтобы прочли другие, но и для того, чтобы прочел «я сам» и зафиксировал бы сам для себя свою же мысль. Но, выведя мысль в текст, я все равно вынужден держать в уме соотношения понятий. В схеме я вывожу мысль «вовне» уже с наглядными понятийными соотношениями.

Так что, во-первых, принимаем усложнения в схемах как неизбежность. А как иначе наглядно отобразить переплетение всех аспектов? Мы другой возможности не видим. Во-вторых, оцениваем их положительно: это лучше, чем описание словами и представление в уме. В-третьих, не пугаемся — это только вначале, с непривычки кажется сложным, а дальше будет легче.

Выше, на «рыбном» примере, мы показали, как пересекаются 4 классификационных аспекта, но можно добавить еще аспекты деления. Ведь рыбы делятся также на съедобных и несъедобных, на дешевых и дорогостоящих, на декоративных и промысловых. Да мало ли еще что придет на ум. Но если надо, то надо. Как же тогда быть с логико-графическим структурированием? Загромождать и без того уже перегруженные структуры, которые у нас уже есть? Можно, но стоит ли это делать? Гештальты теряются. Обычно классификация проводится в каких-то явно существенных научных аспектах, и ученые удовлетворяются двумя-тремя. Ну как с таблицей Менделеева. Поэтому на случай, если все-таки напрашиваются еще какие-то важные и все же научные деления, мы предлагаем делать дополнительные классификационные логико-графические схемы и классифицировать данное явление по двум и более схемам одновременно.

И для нас сейчас важно утвердиться во мнении, что дело классификации упирается в логико-графическое структурирование. Без него можно только все представлять в уме, и в уме скоро получается каша...

Здесь остановимся на таком аспекте проблемы. Классификация предполагает родовидовое деление в сторону конкретизации и в сторону обобщения.

2. ПРОБЛЕМА ОПРЕДЕЛЕНИЯ ПОНЯТИЙ. В любой науке много усилий тратится на определения. В логике говорят об объеме и содержании понятия. Мы ставим некоторые пределы, границы, «концы» в том, что входит в данное понятие. Вот как раз перечисление того, что входит в понятие – это его объем. А содержание понятия – в том, какими признаками описываются его пределы, границы. Некоторые полагают, что они дали определение, а на самом деле предложили лишь тавтологию, например: треугольник – это то, что имеет три угла, дефиниция – это определение. Часто все сводится к описанию составных частей. Гидросфера Земли – это реки, озера, моря и океаны, пар и облака, Или четырехугольники – это прямоугольники, квадраты, ромбы, трапеции.

Большая часть ученых понимают под определением понятие (видовое) подводимое под более общее понятие (родовое), и описываются признаки, отличающие определяемый вид от других видов данного рода. Схематически определения так и будем давать: в одной фигуре – «определяемое», в другой – «определяющие» слова. Между ними в расширении связующей линии с жирными точками по концам – знак равенства. В сущности, и там, и там одно и то же понятие, только обозначенное разными словами. Все это будит и дисциплинирует мысль. В схемах имеет смысл подчеркивать связь определений и классификаций. Излагая классификацию, тут же давать определения входящим в нее понятиям.

3. ЦЕЛОЕ И ЧАСТИ. В научных и учебных материалах, наверное, наравне с родовидовым соотношением понятий встречается соотношение целого и его частей. Все, ну буквально все состоит из частей. В ряде ситуаций это соотношение может быть отображено изоморфно. То есть части и целое представлены, как в реальном предмете, пусть и менее подробно, но похожими на свой прототип. Банальным и в то же время ярким примером может здесь быть условное изображение фигуры человека в детском варианте: «палка, палка, огуречик – вот и вышел человечек». При изоморфном отображении тоже должна учитываться психология восприятия. Части должны восприниматься как фигуры, хорошо выделяемые из фона. Для этого следует иногда пожертвовать натуралистичностью изображения.

Но части и целое не всегда могут быть отображены изоморфно. Национальный состав учащихся в школе, химический состав морской воды, фауна леса... Здесь поможет известный уже нам способ – включение меньших рамок в большую. И здесь опять должно выполняться главное правило – легкость выделения фигуры из фона, роль которого играют другие окружающие фигуры.

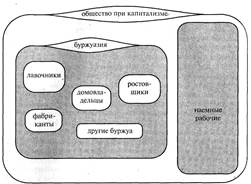Запишем схематично фразу: «Когда заканчивается эксплуатация рабочего фабрикантом, и рабочий получает наличными свою заработную плату, на него набрасываются другие части буржуазии – домовладелец, лавочник, ростовщик и т.п.» (см. рис. 45).

Рис. 45

В соответствии с принципом «разное представлено по-разному» буржуазия дана светло-серой заливкой, наемные работники – темной, буржуазия и ее части – горизонтальными фигурами, наемные рабочие – вертикальной фигурой. Но и то, и другое – в прямоугольных рамках со скругленными углами (одинаковое – одинаково: и то, и другое представляют собой части целого). Отдельные части буржуазии (лавочники, домовладельцы, фабриканты...) представлены одинаково белыми прямоугольниками со скругленными углами и отличаются от целого, у которого светло-серая заливка. А соотношение частей и целого мы отобразили соотношением прямоугольных рамок со скругленными углами, в отличие от родовидового соотношения, где были овалы.

Но в виде частей и целого мы можем представить многое. Например, совокупность действий, не связанных друг с другом временной последовательностью. Скажем, такая деятельность, как уборка квартиры. Тогда: целое – уборка квартиры, а части – мытье посуды, протирание пыли, подметание. Как части можно рассматривать временные последовательности в природных или исторических циклах. Весну, лето, осень, зиму можно считать частями годового цикла как целого (см. рис. 46).

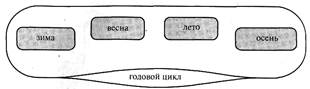
Рис. 46

Зима, конечно, входит в состав только годового цикла, а вот дуб может быть частью дубравы и смешанного леса. Таким образом, соотношение «часть и целое» имеет еще один поворот: не одно целое из нескольких частей, а часть входит в несколько целостных структур, пример – соотношение двух медицинских наук: невропатологии и психиатрии. Обе они — целостные структуры, в каждую из которых входит равноправной составляющей глава «Неврозы» (см. рис. 47).

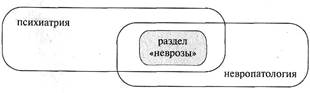
Рис. 47

Не правда ли, похоже на перекресты в классификационных логико-графических структурах? И все же это другое. Так же, как в классификационных схемах, могут быть достаточно сложные хитросплетения понятийных рамок. Ведь одна и та же «часть» может входить в несколько целостных структур (см. рис. 48).

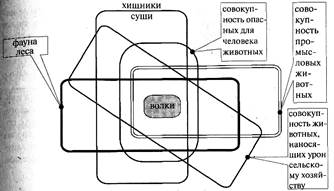
Рис. 48

Дата добавления: 2015-05-26