Определения и простейшие свойства

Термин отсутствует

Нет термина

Метрологическая служба и ее деятельность

Понятия, относящиеся к метрологической службе

(11.2.) Единство измерений (uniformity of measurement)- состояние измерений, при котором их результаты выражены в узаконенных единицах,

(12.1.) Единство измерений (traceability)- состояние измерений, характеризующееся тем, что их результаты выражаются в узаконенных единицах,

погрешности измерений известны с заданной вероятностью.

размеры которых выражаются в узаконенных единицах, размеры которых в установленных пределах равны размерам единиц, воспроизводимых первичными эталонами, а погрешности результатов измерений известны и с заданной вероятностью не выходят за установленные пределы.

(12.2.) Обеспечение единства измерений -деятельность метрологических служб, направленных на достижение и поддержание единства измерений в соответствии с законодательными актами, а также правилами и нормами, установленными государственными стандартами и другими нормативными документами по обеспечению единства измерений.

(11.1.) Метрологическая служба (metrological service) - сеть государственных и ведомственных метрологических органов и их деятельность, направленная на обеспечение единства измерений и единообразия средств измерений в стране.

(12.4.) Метрологическая служба (service of legal metrology) - служба, создаваемая в соответствии с законодательством для выполнения работ по обеспечению единства измерений и для осуществления метрологического контроля и надзора.

(11.3.) Единообразие средств измерений (uniformity of measuring instruments) - состояние средств измерений, характеризующееся тем, что они проградуированы в узаконенных единицах и их метрологические свойства соответствуют нормам.

(11.6.) Поверка средств измерений -определение метрологическим органом погрешностей средств измерений и установление его пригодности к применению.

(12.15.) Поверка средств измерений (verifi-cation) - установление органом метрологической службы (или другим официально уполномоченным органом, организацией) пригодности средств измерений к применению на основании экспериментально определяемых метрологических характеристик и подтверждения их соответствия установленным обязательным требованиям.

Определение 1. Пусть a, b Î Z, m Î N. Говорят, что число а сравнимо с b по модулю m, если а и b при делении на m дают одинаковые остатки. Запись этого факта выглядит так: a º b(mod m).

Определение 2. Два целых числа a и b называются сравнимыми по модулю m, если их разность делится нацело на m. (a-b) ⋮ m

Определение 3. Два целых числа a и b называются сравнимыми по модулю m, если a = b + mt, где tÎZ

Очевидно, что бинарное отношение сравнимости º_m (неважно, по какому модулю) есть отношение эквивалентности на множестве целых чисел.

Ясно, что число а сравнимо с b по модулю m тогда и только тогда, когда а-b делится на m нацело. Очевидно, это, в свою очередь, бывает тогда и только тогда, когда найдется такое целое число t, что a=b+mt.

Понять процесс собирания целых чисел в классы сравнимых между собой по модулю m (классы эквивалентности º_m) поможет следующая картинка:

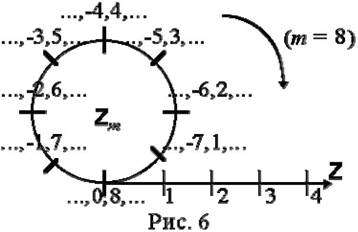
На рисунке 6 изображен процесс наматывания цепочки целых чисел на колечко с m делениями, при этом на одно деление автоматически попадают сравнимые между собой числа. Кстати, эта картинка неплохо объясняет и термин "кольцо".

Перечислим, далее, свойства сравнений, похожие на свойства отношения равенства.

Свойство 1. Сравнения по одинаковому модулю можно почленно складывать.

Доказательство. Пусть a₁= b₁(mod m), a₂= b₂(mod m). Это означает, что a₁ =b₁ +mt₁, a ₂ =b ₂ +mt ₂. После сложения последних двух равенств получим a₁ +a₂ =b₁ +b₂ +m(t₁ +t₂), что означает a₁+a₂ = b₁+b₂(mod m).

Свойство 2. Слагаемое, стоящее в какой-либо части сравнения, можно переносить в другую часть, изменив его знак на обратный.

Доказательство.

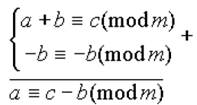
Свойство 3. К любой части сравнения можно прибавить любое число, кратное модулю.

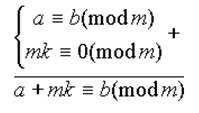Доказательство.

Свойство 4. Сравнения по одинаковому модулю можно почленно перемножать и, следовательно,

Свойство 5. Обе части сравнения можно возвести в одну и ту же степень. Доказательство.

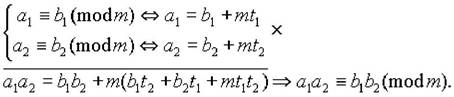
Как следствие из вышеперечисленных свойств, получаем

Свойство 6. Если

a ₀ ≡ b ₀ (mod m), a ₁ ≡ b ₁ (mod m),..., a _n ≡ b _n (mod m), x ≡ y(mod m),

то a ₀ x ⁿ +a ₁ x ^n-1 +...+a _n ≡ b ₀ y ⁿ +b ₁ y ^n-1 +...+b _n (mod m)

Свойство 7. Обе части сравнения можно разделить на их общий делитель, взаимно простой с модулем.

Доказательство. Пусть a ≡ b(mod m), a=a ₁ d, b=b ₁ d. Тогда (a ₁ -b ₁) ⋅ d делится на m.

Поскольку d и m взаимно просты, то на m делится именно (a ₁ -b ₁), что означает a ₁ ≡ b ₁(mod m).

Свойство 8. Обе части сравнения и его модуль можно умножить на одно и то же целое число или разделить на их общий делитель.

Дата добавления: 2015-05-26