Теорема Эйлера и теорема Ферма

Теорема (Эйлера). Пусть m>1, (a,m)=1, ϕ (m) – функция Эйлера. Тогда:

a ^{ϕ (m)} ≡ 1(mod m).

Теорема (Ферма). Пусть р – простое число, р не делит a. Тогда:

a ^p-1 ≡ 1(mod p).

Следствие 1. Без всяких ограничений на a ∈ Z,

a ^p ≡ a(mod p).

Следствие 2. (a+b) ^p ≡ a ^p +b ^p (mod p).

Пример 1. Девятая степень однозначного числа оканчивается на 7. Найти это число.

Решение. a⁹ ≡ 7(mod 10) – это дано. Кроме того, очевидно, что (7, 10)=1 и (a, 10)=1. По теореме Эйлера, a ^ϕ(10) ≡ 1(mod 10). Следовательно, a ⁴ ≡ 1(mod 10) и, после возведения в квадрат, a ⁸ ≡ 1(mod 10). Поделим почленно a ⁹ ≡ 7(mod 10) на a ⁸ ≡ 1(mod 10) и получим a

≡ 7(mod 10). Это означает, что a=7.

Пример 2. Доказать, что 1 ¹⁸ +2 ¹⁸ +3 ¹⁸ +4 ¹⁸ +5 ¹⁸ +6 ¹⁸ ≡ -1(mod 7)

Доказательство. Числа 1, 2, 3, 4, 5, 6 взаимно просты с 7. По теореме Ферма имеем:

Возведем эти сравнения в куб и сложим:

1 ¹⁸ +2 ¹⁸ +3 ¹⁸ +4 ¹⁸ +5 ¹⁸ +6 ¹⁸ ≡ 6(mod 7) ≡ -1(mod 7)

Пример 3. Найти остаток от деления 7 ⁴⁰² на 101.

Решение. Число 101 – простое, (7, 101)=1, следовательно, по теореме Ферма: 7¹⁰⁰ ≡ 1(mod 101). Возведем это сравнение в четвертую степень: 7 ⁴⁰⁰ ≡ 1(mod 101), домножим его на очевидное сравнение 7 ² ≡ 49(mod 101), получим: 7 ⁴⁰² ≡ 49(mod 101). Значит, остаток от деления 7 ⁴⁰² на 101 равен 49.

Пример 4. Найти две последние цифры числа 243 ⁴⁰².

Решение. Две последние цифры этого числа суть остаток от деления его на 100. Имеем: 243=200+43; 200+43 ≡ 43(mod 100) и, возведя последнее очевидное сравнение в 402-ую степень, раскроем его левую часть по биному Ньютона (мысленно, конечно). В этом гигантском выражении все слагаемые, кроме последнего, содержат степень числа 200, т.е. делятся на 100, поэтому их можно выкинуть из сравнения, после чего понятно, почему 243 ⁴⁰² ≡ 43⁴⁰² (mod 100).

Далее, 43 и 100 взаимно просты, значит, по теореме Эйлера, 43 ^{ϕ (100)} ≡ 1(mod 100). Считаем:

ϕ (100)= ϕ (2 ² ⋅ 5 ²)=(10–5)(10–2)=40.

Имеем сравнение: 43 ⁴⁰ ≡ 1(mod 100), которое немедленно возведем в десятую степень и умножим почленно на очевидное сравнение, проверенное на калькуляторе: 43 ² ≡ 49(mod 100).

Получим:

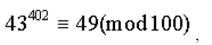
следовательно, две последние цифры числа 243 ⁴⁰² суть 4 и 9.

Пример 5. Доказать, что (73 ¹² -1) делится на 105.

Решение. Имеем: 105=3 ⋅ 5 ⋅ 7, (73,3)=(73,5)=(73,7)=1. По теореме Ферма:

73 ² ≡ 1(mod 3)

73 ⁴ ≡ 1(mod 5)

73 ⁶ ≡ 1(mod 7)

Перемножая, получаем:

73 ¹² ≡ 1(mod 3),(mod 5),(mod 7),

откуда, по свойствам сравнений, изложенным в пункте 16, немедленно следует:

73 ^{12 -1} ≡ 0(mod 105),

ибо 105 - наименьшее общее кратное чисел 3, 5 и 7. Именно это и требовалось.

Дата добавления: 2015-05-26