Функция Эйлера

Функция Эйлера ϕ (a) есть количество чисел изряда 0, 1, 2,..., a - 1, взаимно простых с a.

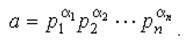Лемма. Пусть

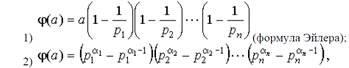Тогда:

в частности, φ(p ^α) = p ^α - p ^α-1, φ (p) = p - 1.

Пример. Пусть m = 42. Тогда приведенная система вычетов суть:

1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.

Лемма 2. 1) Любые ϕ (m) чисел, попарно не сравнимые по модулю m и взаимно простые с модулем, образуют приведенную систему вычетов по модулю m.

2) Если (a,m) = 1 и x пробегает приведенную систему вычетов по модулю m, то аx так же пробегает приведенную систему вычетов по модулю m.

Доказательство. Утверждение 1) – очевидно. Докажем утверждение 2). Числа аx попарно несравнимы (это доказывается так же, как в лемме 1 этого пункта), их ровно ϕ (m) штук. Ясно также, что все они взаимно просты с модулем, ибо (a,m)=1, (x,m)=1 ⇒ (ax.m)=1. Значит, числа аx образуют приведенную систему вычетов.

Лемма 3. Пусть m₁, m₂,..., m_k – попарно взаимно просты и m₁ m₂...m_k =M₁m₁ =M₂ m₂=...=M_k m_k, где M_j =m₁...m_j-1 m_j+1...m_k

1) Если x₁, x₂,..., x_k пробегают полные системы вычетов по модулям m₁, m₂,..., m_k соответственно, то значения линейной формы M₁ x₁ +M₂ x₂ +...+M_kx_k пробегают полную систему вычетов по модулю m= m₁ m₂...m_k.

2) Если ξ ₁, ξ ₂,..., ξ _k пробегают приведенные системы вычетов по модулям m₁, m₂,..., m_k соответственно, то значения линейной формы M₁ ξ ₁ +M₂ ξ ₂ +...+M _k ξ _k пробегают приведенную систему вычетов по модулю m= m₁ m₂...m_k.

Лемма 4. Пусть x₁, x₂,..., x_k , x пробегают полные, а ξ ₁ , ξ ₂,..., ξ _k, ξ – пробегают приведенные системы вычетов по модулям m ₁, m ₂,..., m _k и m=m₁ m₂...m_k соответственно, где (m _i m _j)=1 при i ≠ j. Тогда дроби {x₁ /m₁ +x ₂ /m ₂ +...+x _k /m _k } совпадают с дробями {x/m}, а дроби { ξ ₁ /m ₁ + ξ ₂ /m ₂ +...+ ξ _k /m _k } совпадают с дробями { ξ /m}.

Обозначим через ε k k -ый корень m- ой степени из единицы:

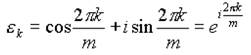
Здесь k=0,1,...,m-1 – пробегает полную систему вычетов по модулю m.

Напомню, что сумма ε ₀ + ε ₁ +...+ ε _m-1 всех корней m -ой степени из единицы равна нулю для любого m. Действительно, пусть ε ₀ + ε ₁+...+ ε _m-1 =a. Умножим эту сумму на ненулевое число ε 1. Такое умножение геометрически в комплексной плоскости означает поворот правильного m -угольника, в вершинах которого расположены корни ε ₀ + ε ₁ +...+ ε _m-1, на ненулевой угол 2 π /m. Ясно, что при этом корень ε ₀ перейдет в корень ε ₁, корень ε ₁ перейдет в корень ε ₂, и т.д., а корень ε _m-1 перейдет в корень ε ₀, т.е. сумма ε ₀ + ε ₁ +...+ ε _m-1 не изменится. Имеем ε ₁ a=a, откуда a=0.

Теорема 1. Пусть m>0 - целое число, a ∈ Z, x пробегает полную систему вычетов по

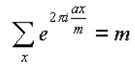модулю m. Тогда, если а кратно m, то

в противном случае, при а не кратном m,

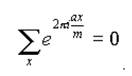
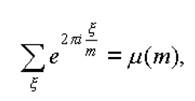Теорема 2. Пусть m>0 – целое число, ξ пробегает приведенную систему вычетов по модулю m. Тогда (сумма первообразных корней степени m):

где μ(m) – функция Мебиуса.

Дата добавления: 2015-05-26