Сравнения первой степени

Рассмотрим сравнения первой степени вида

ax ≡ b(mod m),

Как решать такое сравнение? Рассмотрим два случая.

Случай 1. Пусть а и m взаимно просты. Тогда несократимая дробь m/a сама просится разложиться в цепную дробь:

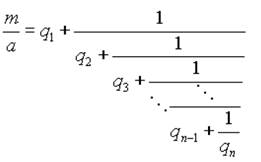
Эта цепная дробь, разумеется, конечна, так как m/a - рациональное число. Рассмотрим две ее последние подходящие дроби:

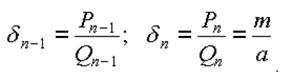
Вспоминаем важное свойство числителей и знаменателей подходящих дробей: mQ_n-1 -aP _n-1 =(-1) ⁿ. Далее (слагаемое mQ _n-1, кратное m, можно выкинуть из левой части

сравнения):

-aP _n-1 ≡ (-1) ⁿ (mod m) т.е.

aP _n-1 ≡ (-1) ^n-1 (mod m) т.е.

a[(-1) ^n-1 P _n-1 b] ≡ b(mod m)

и единственное решение исходного сравнения есть:

x ≡ (-1) ^n-1 P _n-1 b(mod m)

Пример. Решить сравнение 111x ≡ 75(mod 322).

Решение. (111, 322)=1. Включаем алгоритм Евклида:

322=111 · 2+100

111=100 · 1+11

100=11 · 9+1

11=1 · 11

(В равенствах подчеркнуты неполные частные.) Значит, n=4, а соответствующая цепная

дробь такова:

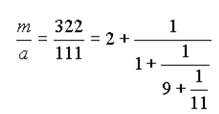
Посчитаем числители подходящих дробей, составив для этого стандартную таблицу:

Числитель предпоследней подходящей дроби равен 29, следовательно, готовая формула

дает ответ: x ≡ (-1) ³ ⋅ 29 ⋅ 75 ≡ -2175 ≡ 79(mod 322)

Случай 2. Пусть (a,m)=d. В этом случае, для разрешимости сравнения ax ≡ b(mod m)

необходимо, чтобы d делило b, иначе сравнение вообще выполняться не может.

Действительно, ax ≡ b(mod m) бывает тогда, и только тогда, когда ax- b делится на m нацело, т.е.

ax- b=t · m, t ∈ Z, откуда b=ax- t ⋅ m, а правая часть последнего равенства кратна d.

Пусть b=db₁, a=da₁, m=dm₁. Тогда обе части сравнения xa₁d ≡ b₁d(mod m₁d) и его модуль поделим на d:

xa₁ ≡ b₁ (mod m₁),

где уже а₁ и m₁ взаимно просты. Согласно случаю 1 этого пункта, такое сравнение имеет единственное решение x₀:

x ≡ x₀ (mod m₁) (*)

По исходному модулю m, числа (*) образуют столько решений исходного сравнения, сколько чисел вида (*) содержится в полной системе вычетов: 0,1,2,..., m-2, m-1. Очевидно, что из чисел x = x₀ + t ⋅ m в полную систему наименьших неотрицательных вычетов попадают только x₀, x₀ + m₁, x₀ +2m₁,..., x₀ +(d-1)m₁, т.е. всего d чисел. Значит у исходного сравнения имеется d решений.

Подведем итог рассмотренных случаев в виде следующей теоремы

Теорема 1. Пусть (a,m)=d. Если b не делится на d, сравнение ax ≡ b(mod m) не имеет решений. Если b кратно d, сравнение ax ≡ b(mod m) имеет d штук решений.

Пример. Решить сравнение 111x ≡ 75(mod 321).

Решение. (111,321)=3, поэтому поделим сравнение и его модуль на 3:

37x ≡ 25(mod 107) и уже (37,107)=1.

Включаем алгоритм Евклида (как обычно, подчеркнуты неполные частные):

107=37 ⋅ 2+33

37=33 ⋅ 1+4

33=4 ⋅ 8+1

4=1 ⋅ 4

Имеем n=4 и цепная дробь такова:

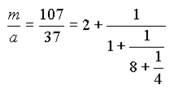
Таблица для нахождения числителей подходящих дробей:

Значит, x ≡ (-1) ³ ⋅ 26 ⋅ 25 ≡ -650(mod 107) ≡ -8(mod 107) ≡ 99(mod 107).

Три решения исходного сравнения:

x ≡ 99(mod 321), x ≡ 206(mod 321), x ≡ 313(mod 321),

и других решений нет.

Теорема 2. Пусть m>1, (a,m)=1 Тогда сравнение ax ≡ b(mod m) имеет решение: x ≡ ba ^{ϕ (m)-1}(mod m).

Пример. Решить сравнение 7x ≡ 3(mod 10). Вычисляем:

ϕ (10)=4; x ≡ 3 ⋅ 7 ^4-1 (mod 10) ≡ 1029(mod 10) ≡ 9(mod 10).

Видно, что этот способ решения сравнений хорош (в смысле минимума интеллектуальных затрат на его осуществление), но может потребовать возведения числа а в довольно большую степень, что довольно трудоемко. Для того, чтобы как следует это прочувствовать, возведите самостоятельно число 24789 в степень 46728.

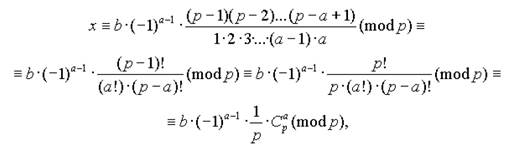Теорема 3. Пусть р – простое число, 0<a<p. Тогда сравнение ax ≡ b(mod p) имеет решение:

где 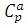– биномиальный коэффициент.

Пример. Решить сравнение 7x ≡ 2(mod 11). Вычисляем:

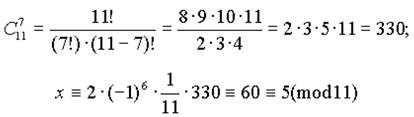
Лемма 1 (Китайская теорема об остатках). Пусть дана простейшая система сравнений первой степени:

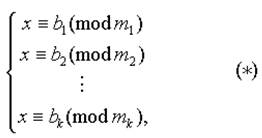
где m ₁,m ₂,...,m _k попарно взаимно просты. Пусть, далее, m ₁ m ₂...m _k =M_s m_s; M _s M _s ^∇ ≡ 1(mod m_s) (Очевидно, что такое число M _s ^∇ всегда можно подобрать хотя бы с помощью алгоритма Евклида, т.к. (m_s,M_s)=1); x₀ =M₁M₁ ^∇ b₁ +M₂M₂ ^∇ b₂ +...+M_kM_k ^∇ b_k. Тогда система (*) равносильна одному сравнению x ≡ x₀ (mod m₁ m₂...m_k), т.е. набор решений (*) совпадает с набором решений сравнения x ≡ x₀ (mod m₁ m₂...m_k).

Пример. Однажды средний товарищ подошел к умному товарищу и попросил его найти число, которое при делении на 4 дает в остатке 1, при делении на 5 дает в остатке 3, а при делении на 7 дает в остатке 2. Сам средний товарищ искал такое число уже две недели. Умный товарищ тут же составил систему:

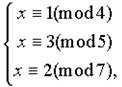
которую начал решать, пользуясь леммой 1. Вот его решение:

b ₁ =1; b ₂ =3; b ₃ =2; m ₁ m ₂ m ₃, т.е. M ₁ =35, M ₂ =28, M ₃ =20.

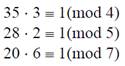Далее он нашел:

т.е. M ₁ ^∇ =3, M ₂ ^∇ =2, M ₃ ^∇ =6. Значит x ₀ =35 ⋅ 3 ⋅ 1+28 ⋅ 2 ⋅ 3+20 ⋅ 6 ⋅ 2=513. После этого, по лемме 1, умный товарищ сразу получил ответ:

x ≡ 513(mod 140) ≡ 93(mod 140),

т.е. наименьшее положительное число, которое две недели искал средний товарищ, равно 93. Так умный товарищ в очередной раз помог среднему товарищу.

Лемма 2. Если b ₁,b ₂,...,b _k пробегают полные системы вычетов по модулям m ₁,m ₂,...,m _k соответственно, то x ₀ пробегает полную систему вычетов по модулю m ₁ m ₂...m _k.

Дата добавления: 2015-05-26