
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Градуировочная функция
|
|
|
|
Часто в аналитических измерениях при определении концентрации соединений рядом методов, таких как хроматография, фотометрия и др. используют метод абсолютной калибровки, который предполагает установление концентрации соединения по градуировочному графику. Для этого из стандартных образцов или чистых реактивов готовят градуировочные растворы с известной концентрацией анализируемого соединения (xi) и измеряют их соответствующие отклики (yi).
На основании результатов измерений (yi) градуировочных растворов и значений концентрации соединений в растворах (xi) строят градуировочный график, откладывая по оси абсцисс концентрацию соединения в градуировочных растворах хi, а по оси ординат – соответствующее измеренное значение отклика yi.
Уравнение градуировочной характеристики обычно имеет линейный вид:
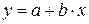 , (19)
, (19)
где a – точка пересечения градуировочного графика с осью ординат;
b – угловой коэффициент линейного градуировочного графика.
Коэффициенты a и b и коэффициент их корреляции r(a,b) находят методом наименьших квадратов по формулам:
 (20)
(20)
 (21)
(21)
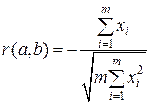 (22)
(22)
где xi – концентрация вещества в i -том градуировочном растворе;
yi – измеренный отклик i -того градуировочного раствора;
m – количество пар точек, используемых для построения градуировочного графика (количество градуировочных растворов, умноженное на число повторных измерений, выполненных для каждого из них);
i – индекс точки, i =1, 2, …, m.
Также возможно нахождение коэффициентов а и b с помощью программы «Microsoft Office Excel 2003». Для этого необходимо выделить две ячейки, обратиться к мастеру функций, выбрать функцию «ЛИНЕЙН», заполнить появившееся диалоговое окно соответствующими значениями х и y. В результате вычисленное значение появится только в одной ячейке и будет соответствовать коэффициенту b. Для того чтобы вычисленное значение a появилось в другой ячейке необходимо войти в режим редактирования, нажав клавишу «F2», а затем нажать комбинацию клавиш «CTRL+SHIFT+ENTER».
Полученная линейная градуировочная зависимость используется затем для вычисления концентрации соединения xизм. в исследуемом растворе, которую дает наблюдаемый отклик yизм .:
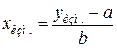 (23)
(23)
При нахождении неопределенности концентрации соединения (xизм.) рассматривают следующие основные источники неопределенности (рис. 13):
а) случайные эффекты, результатом которых являются погрешности приписанных исходных значений концентраций градуировочных растворов xi.;
б) случайные колебания при измерении y, которые оказывают влияние как на отклики при градуировке yi, так и на измеряемый отклик yизм..
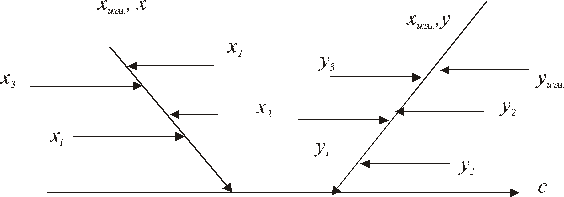
Рис. 13. Источники неопределенности при определении концентрации методом абсолютной калибровки
Оценивание неопределенности u(xизм., x), обусловленной неопределенностями приписанных исходных значений концентраций градуировочных растворов xi проводится в зависимости от того, каким образом осуществлялось приготовление градуировочных растворов (пример 1–5).
Оценивание неопределенности u(xизм, y.), обусловленной случайными колебаниями величины y, можно осуществить несколькими способами.
Способ 1. По рассчитанной дисперсии и ковариации:
 (24)
(24)
где So – стандартное отклонение разностей между экспериментальной величиной и найденной зависимостью (по оси ординат);
S(a) – стандартная неопределенность оцененная на основании результатов измерений величины отрезка а, отсекаемого на оси ординат;
S(b) – стандартная неопределенность оцененной величины b;
k – количество измерений при определении xизм..
Величины So, S(a), S(b) находят по методу наименьших квадратов по следующим формулам:
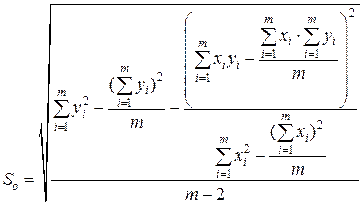 (25)
(25)
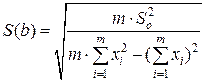 (26)
(26)
 , (27)
, (27)
Способ 2. По данным градуировки:
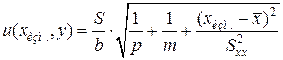 (28)
(28)
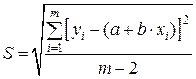 (29)
(29)
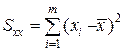 , (30)
, (30)
где 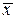 – среднее значение для концентрации градуировочных растворов;
– среднее значение для концентрации градуировочных растворов;
p – число измерений при определении хизм..
Способ 3. На основе информации, которую дают компьютерные программы при нахождении градуировочных зависимостей.
Многие программы вычисляют S, выраженное, например, в виде относительного среднего квадрата (RMS) или остаточного стандартного отклонения. Эти данные можно использовать в уравнении (73). Некоторые программы вычисляют также стандартное отклонение S(yс.) значения y, вычисленного по градуировочному графику для некоторого нового значения x и его можно использовать для вычисления u(xизм, y.).
Расчет суммарной стандартной неопределенности определяемой концентрации соединения в испытуемом растворе u(xизм.) осуществляется суммированием неопределенностей, оцененных исходя из указанных двух источников:
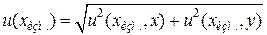 (31)
(31)
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 5224; Нарушение авторских прав?; Мы поможем в написании вашей работы!