Погрешность шкальных приборов

При проведении испытаний с помощью шкальных приборов стандартная неопределенность включает в себя два вклада:

1) вклад из-за погрешности средства измерения информация, о которой приведена в свидетельствах о калибровке, документации производителя или стандартах;

2) вклад из-за ошибки оператора при снятии показаний со шкалы средства измерения (рис. 14).

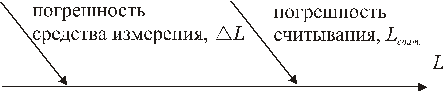
Рис. 14. Источники неопределенности при измерении на шкальных приборах

Ошибка оператора при снятии показаний со шкалы средства измерений не учитывается, если проводятся повторные измерения одной и той же величины, и вычисляется неопределенность типа А. В этом случае погрешность считывания попадет в число случайных отклонений, охватываемых неопределенностью типа А.

Пример 8. Необходимо рассчитать стандартную неопределенность длины образца, которую определяли при помощи линейки 300 ГОСТ 427-75 с ценой деления 1 мм и допускаемой погрешностью измерения ±0,1 мм.

Стандартную неопределенность измерения рассчитывают исходя из прямоугольного закона распределения и пределов допускаемой погрешности измерения ±0,1 мм:

мм

Вклад из-за ошибки оператора при снятии показаний со шкалы линейки также рассчитывается исходя из прямоугольного закона распределения по формуле:

мм,

где

мм

Эти два вклада суммируют, получая стандартную неопределенность измерения длины образца:

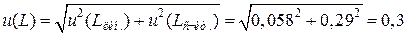мм

Дата добавления: 2015-05-26