Бюджет неопределенности концентрации раствора гидроксида натрия

№	Наименование величины	Обозначение величины	Единица измерения	Значение величины	Тип неопределенности	Вид распределения	Стандартная неопределенность u(xi)	Относительная стандартная неопределенность	Процентный вклад Z, %
	Масса навески	m	г	30,24	B	прямоугольное	0,003	9,9·10^-5	0,01
	Степень чистоты NaOH	P	-		B	прямоугольное	0,0058	0,0058	36,3
	Объем раствора	V	л	0,1	B	треугольное / прямоугольное	0,00073	0,0073	57,5

Продолжение табл. 7

	Молярная масса NaOH	Mr	г/моль	39,9971	B	прямоугольное	0,00017	4,3·10^-6	1,8·10^-5
	Повторяемость	δ	моль/л	7,48	A	нормальное	0,018	0,0024	6,1

Как видно из таблицы, наибольший вклад вносит неопределенность, возникающая из-за ошибки объема, в котором растворяют гидроксид натрия.

Пример 11. Определить расширенную неопределенность измерения разрывной нагрузки ткани хлопчатобумажной при растяжении по утку по ГОСТ 3813-72. Из точечной пробы вырезали 5 образцов размером 50×200 мм, испытания проводили на разрывной машине (допускаемая погрешность измерения нагрузки 1%), использовали линейку длиной 300 мм с ценой деления 1 мм по ГОСТ 427-75. Результаты измерений разрывной нагрузки: F₁ =835 Н; F₂ =850 Н; F₃ =872 Н; F₄ =844 Н; F₅ =880 Н. За разрывную нагрузку точечной пробы принимают среднеарифметическое значение результатов измерений пяти образцов.

Неопределенность будет включать в себя 4 вклада:

1) Вклад из-за погрешности измерения длины образца u(L_(длина));

2) Вклад из-за погрешности измерения ширины образца u(L_{(ширина)});

3) Неопределенность разрывной нагрузки, возникающая из-за погрешности ее измерения с помощью разрывной машины u(ΔF);

4) Неопределенность разрывной нагрузки из-за изменчивости измеряемой величины от образца к образцу (стандартная неопределенность повторяемости u(δ)).

Причинно-следственная диаграмма имеет вид (рис. 16)

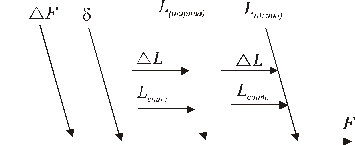
Рис. 16. Источники неопределенности измерений разрывной нагрузки ткани

Стандартные неопределенности измерения длины u(L_(длина)) и ширины u(L_{(ширина)}) образца будут равны, так как при этом использовали одну и ту же линейку 300 ГОСТ 427-75 и их расчет производится в соответствии с примером 8.

Стандартную неопределенность разрывной нагрузки u(ΔF) рассчитывают, предполагая прямоугольное распределение для величины погрешности нагрузки в интервале ±1% по формуле:

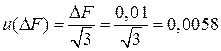
Стандартную неопределенность повторяемости u(δ) в данном случае можно вычислить по типу А по формуле (50) следующим образом:

Н

Суммарная стандартная неопределенность измерения разрывной нагрузки равна:

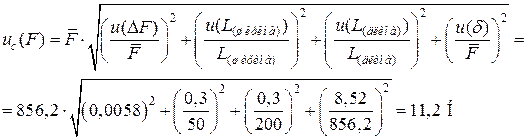
Расширенная неопределенность для уровня доверия 95 % равна:

Таким образом, разрывная нагрузка ткани при растяжении по утку составляет (856,2±22,4)Н, где цифра, следующая за ±, является расширенной неопределенностью, рассчитанной при коэффициенте охвата k = 2 и уровне доверия 95 %.

Бюджет неопределенности, представлен в таблице 8. При этом процентный вклад каждой неопределенности рассчитывается как:

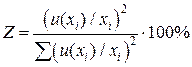(40)

Таблица 8

Дата добавления: 2015-05-26