Уравнение массообмена

Для получения дифференциального уравнения массообмена в движущейся жидкости выделим параллелепипед (рис. 4.1).

За малый промежуток времени dt в параллелепипед через грань, перпендикулярную оси х, вносится масса i -го компонента 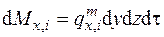, а выносится масса 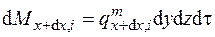. Следовательно, если предположить, что жидкость несжимаема, а внутри параллелепипеда отсутствуют источники массы, то разность масс поступившей и вышедшей вдоль оси х относительно объема параллелепипеда равна

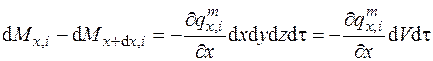. (4.25)

Аналогичные выражения можно записать и в направлении осей y и z.

Если просуммировать изменение массы i -го компонента, проходящей через параллелепипед, то получим

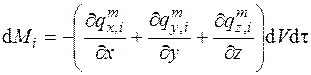. (4.26)

Необходимо учесть, что d M_i в (4.26) можно записать по-другому:

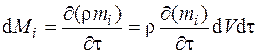. (4.27)

Подставляя выражение (4.27) в (4.26), получим

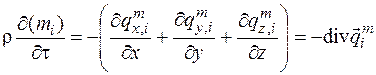. (4.28)

Будем полагать, что перенос массы осуществляется только за счет концентрационной диффузии и конвекции. Тогда плотность потока массы вдоль оси х математически можно записать следующим образом:

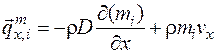. (4.29)

Аналогично выражению (4.29) записываются плотности потоков массы вдоль осей y и z. Причем, первый член в правой части выражения (4.29) дает плотность потока массы за счет концентрационной диффузии, а второй – за счет конвекции.

Далее необходимо все выражения типа (4.29) подставить в выражение (4.28), но с учетом того, что для оси х

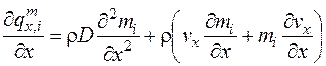, (4.30)

аналогично и для осей y и z. Тогда будем иметь

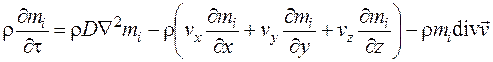. (4.31)

В выражении (4.31) учтем, что при r = const, .

Если второй член из правой части выражения (4.31) перенести в левую часть, то сумму частных производных по времени и координатам можно заменить производной по времени, и с помощью оператора градиент набла Ñ записать полученное выражение в виде

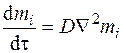. (4.32)

Выражение (4.32) и является дифференциальным уравнением массопереноса.

Если конвекция отсутствует, v_x = v_y = v_z = 0, то есть существует только концентрационная диффузия, то из выражения (4.32) получаем уравнение

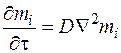, (4.33)

которое является уравнением Фика. Оно аналогично дифференциальному уравнению теплопроводности.

Для формулирования краевой задачи тепло- и массообмена к системе дифференциальных уравнений переноса энергии и массы необходимо добавить начальные и граничные условия.

Необходимо иметь в виду, что конвективный массообмен – это перенос массы за счет молекулярной диффузии и конвекции.

Глава 5. Теплообменные аппараты

Дата добавления: 2015-05-26