Нестационарная теплопроводность

Такие процессы наблюдаются в твердых телах и жидкостях, когда имеются внутренние источники тепла или в случае изменения распределения температуры в пространстве с течением времени. Подобные процессы наблюдаются при пуске и остановке различных теплообменных аппаратов, нагреве и охлаждении различных изделий и т. д. Все подобные процессы приводят к тому, что система (твердое тело или жидкость) стремится к тепловому равновесию или при этом происходят циклические изменения температуры.

Нестационарные тепловые процессы тесно связаны с изменением внутренней энергии. Запишем дифференциальное уравнение теплопроводности в прямоугольной декартовой системе координат, заменяя в выражении (3.8) 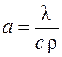, тогда получим

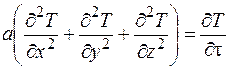. (3.70)

Краевая задача формулируется следующим образом:

1) Задаются начальные условия, то есть распределение температуры в начальный момент времени, при τ = 0.

Т ₀ = f (x, y, z).(3.71)

2) Граничные условия, например, в виде граничных условий третьего рода, когда задается плотность теплового потока, подходящего к границе раздела и отходящего за счет теплоотдачи во внешнюю среду:

. (3.72)

В качестве примера рассмотрим охлаждение плоской пластины, неограниченной по координатам y и z, имеющей толщину 2d (рис. 3.2). Отсчет температуры будем производить относительно жидкости, в которой находится пластина, то есть

.

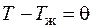Тогда дифференциальное уравнение (3.70) записывается для одномерного случая:

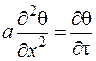. (3.73)

1) Начальные условия при τ = 0 q₀ = F (x), то есть q₀ – функция координаты х.

2) Граничные условия:

а) на оси пластины

х = 0, 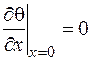; (3.74)

б) на поверхности пластины

х = d, .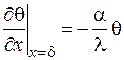

Решение дифференциального уравнения (3.73) с учетом граничных и начальных условий (3.74) дает распределение температуры в пластине по оси х с течением времени.

Для решения уравнения применяется известный метод разделения переменных, так как левая часть зависит только от координаты х, а правая – только от времени t, то есть решение ищется в виде произведения функций:

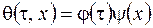. (3.75)

Подставляя формулу (3.75) в формулу (3.73), получим после преобразований систему однородных дифференциальных уравнений, решение которых известно:

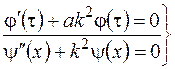, (3.76)

где k – постоянная, которая определяется граничными условиями, причем 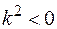, т. е. тепловые процессы стремятся к равновесному состоянию.

Решением для первого уравнения является функция

. (3.77)

Решение второго уравнения можно записать в виде

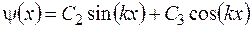. (3.78)

А общее решение системы уравнений (3.76) получится таким:

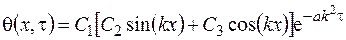. (3.79)

Из граничного условия (3.74) (при х = 0) получим

,

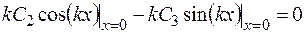следовательно, С ₂ = 0.

Общее решение (3.79) тогда будет следующим:

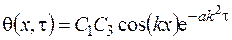. (3.80)

Из граничного условия (3.74) (при х = d) получим

,

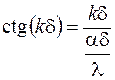но учитывая, что 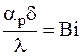и обозначив 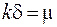, получаем

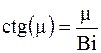. (3.81)

По смыслу m есть угол, который изменяется в пределах [0, p], [p, 2p], [2p, 3p] и так далее. При m = 0, p, 2p, … ctgm ®¥.

При m = p/2, 3p/2, … ctgm = 0. Найдем решение (3.81) графическим способом (рис. 3.3). Для этого левую часть (3.81) обозначим 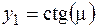, а правую 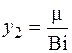, которое представляет уравнение прямой. Решениями будут являться значения m, соответствующие точкам пересечения двух графиков (прямой и котангенса), то есть m₁, m₂, m₃, полученным при определенном значении Bi. Из рис. 3.3 видно, что m₁ < m₂ < m₃.

В уравнении (3.80) произведение постоянных можно обозначить другой постоянной 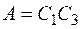, которую можно определить из начальных условий с учетом того, что температура внутри пластины представляет собой сумму решений для 1 < n < ¥, то есть

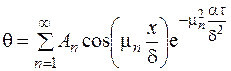. (3.82)

В (3.82) полагаем при t = 0, 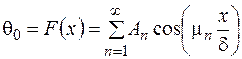, откуда получаем

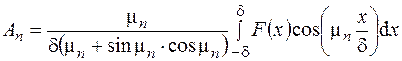. (3.83)

Подставив формулу (3.83) в формулу (3.82), получим окончательное выражение для распределения температуры внутри пластины при ее охлаждении с течением времени.

Анализ показывает, что скорость процесса распространения теплоты в твердых телах зависит от отношения площади поверхности тела к их объему. Скорость будет больше, если это отношение будет расти. При прочих равных условиях эта скорость будет наибольшей для шара.

Если ввести обозначение безразмерной величины 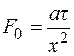– число Фурье, представляющее собой безразмерное время, то для шара d = r, а 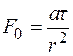, и построить зависимость температуры в центре шара или на оси пластины от числа F ₀, то есть .

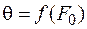Глава 4. Конвективный теплообмен

Дата добавления: 2015-05-26