Передача теплоты через цилиндрическую стенку. а) Найдем распределение температуры в цилиндрической стенке с внутренним диаметром d1 и наружным d2

а) Найдем распределение температуры в цилиндрической стенке с внутренним диаметром d ₁ и наружным d ₂. На поверхностях стенки заданы температуры T _c1 (внутренняя стенка) и T _c2 (внешняя стенка).

Выберем цилиндрическую систему координат, в которой дифференциальное уравнение теплопроводности записывается следующим образом:

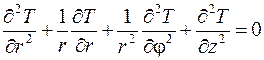. (3.33)

Правая часть выражения (3.33) равна нулю, так как рассматривается стационарное состояние, то есть 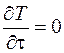. Поскольку температура не зависит от координат φ и z, то уравнение (3.33) записывается для одномерного случая:

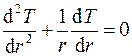. (3.34)

Граничные условия запишутся так:

1) при r = r ₁ T = T _c1; 2) при r = r ₂ T = T _c2.

Для решения (3.34) обозначим первую производную . Тогда будем иметь , а .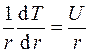

Дифференциальное уравнение (3.34) примет вид

. (3.35)

Решая это уравнение методом разделения переменных, получаем

.

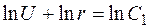Откуда после перехода к первоначальной переменной получаем:

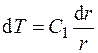. (3.36)

Интегрируя (3.36), получаем:

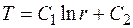. (3.37)

Постоянные С ₁ и С ₂ находим из (3.37) с учетом граничных условий: 1) при r = r ₁ T = T _c1 = С ₁ln r ₁ + C ₂;

2) при r = r ₂ T = T _c2 = С ₁ln r ₂ + C ₂. (3.38)

Из (3.38) получаем

, .

Если подставить выражения для С ₁ и С ₂ в (3.37), то получим формулу для расчета температуры в любой точке цилиндрической поверхности, имеющей радиус r > r ₁, но при этом r > r ₂:

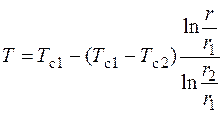. (3.39)

Поскольку функция логарифма является нелинейной, то распределение температуры в цилиндрической стенке является нелинейным. При теплопередаче через цилиндрическую стенку нужно иметь в виду, что плотность теплового потока изменяется с ростом r, так как изменяется площадь поверхности цилиндра. Но при этом нужно учитывать, что количество теплоты, проходящее через цилиндрическую стенку в единицу времени, не зависит от радиуса.

Плотность теплового потока можно рассчитать на единицу внутренней или внешней поверхности трубы:

; (3.40)

, (3.41)

где l – длина рассматриваемого цилиндрического слоя.

Если тепловой поток отнести к единице длины трубы, то получим

. (3.42)

Величина q _l при этом носит название линейной плотности теплового потока.

Закономерность распределения температурного поля в случае, если , где b – постоянная, описывается следующим выражением:

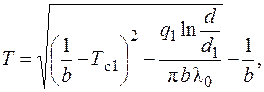(3.43)

где q ₁ – плотность теплового потока, определяется выражением (3.40).

б) Пусть внутри трубы проходит более горячая жидкость с температурой Т ₁, а снаружи трубы проходит жидкость с меньшей температурой Т ₂. Коэффициенты теплоотдачи на внутренней и внешней поверхностях трубы обозначим a₁ и a₂ соответственно. Ставится задача найти линейную плотность теплового потока и температуру стенок Т _с1 и Т _с2.

Для решения задачи запишем линейную плотность теплового потока от внутренней жидкости к стенке 1, затем от внутренней стенки 1 к внешней 2 и от внешней стенки к жидкости, которая находится вне трубы. Тогда на основании (3.42) будем иметь:

; (3.44)

; (3.45)

. (3.46)

После преобразований из (3.44)–(3.46) для q _l получаем следующее выражение:

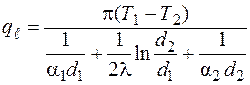. (3.47)

В выражении (3.47) величина

(3.48)

носит название линейного коэффициента теплопередачи. Он численно равен количеству теплоты, которое передается через единицу поверхности стенки от горячей жидкости к холодной в единицу времени при разности температур между горячей и холодной жидкостями в 1 К.

Составляющие коэффициента теплопередачи на внутренней и внешней поверхностях трубы зависят не только от коэффициентов теплоотдачи a₁ и a₂, но и от соответствующих диаметров.

В общем случае

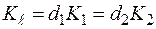, (3.49)

отсюда будем иметь выражение для коэффициентов теплопередачи K ₁ и K ₂ в виде:

; . (3.50)

Термическое сопротивление теплопередачи R _l цилиндрической стенки – это величина обратная K _l, определяемая по (3.48):

. (3.51)

Выясним, как будет изменяться R _l при изменении толщины цилиндрической стенки, то есть возьмем производную от R _l по d ₂:

. (3.52)

Из (3.51) и (3.52) следует, что при увеличении 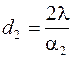термическое сопротивление теплопередачи имеет минимум. Этот диаметр трубы называют критическим.

Если наложить на внешнюю трубу изоляцию диаметром
d ₃ > d ₂, то термическое сопротивление теплопередачи будет выражаться следующим образом:

. (3.53)

Если иметь в виду, что тепловой поток на единицу длины трубы равен

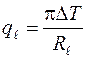, (3.54)

то из (3.53) и (3.54) следует, что при увеличении d ₃ (диаметра изоляции) q _l будет возрастать и при d ₃ = d _кр будет иметь максимум, но потом будет снижаться.

Таким образом, если d ₂ < d ₃ < d _кр, то при увеличении толщины теплоизоляции будет наблюдаться увеличение теплопотерь. Для эффективной работы теплоизоляции должно быть d _кр £ d ₂. Критический диаметр изоляции зависит от ее параметров: .

Дата добавления: 2015-05-26