Дифференциальное уравнение теплопроводности. В большинстве практических случаев представляет интерес температурное поле внутри массивов горных пород или сооружений и механизмов

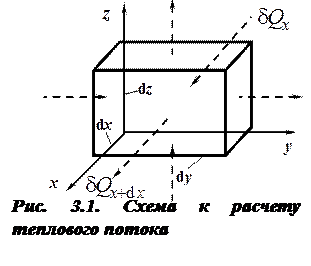
В большинстве практических случаев представляет интерес температурное поле внутри массивов горных пород или сооружений и механизмов. Для этого необходимо иметь дифференциальное уравнение теплопроводности. Для его получения закон сохранения энергии сформулируем следующим образом: количество теплоты d Q, поступившее в элементарный объем за время d τ за счет теплопроводности, а также от внутренних источников, равно изменению внутренней энергии или энтальпии вещества (в зависимости от рассмотрения процессов V = const или p = const), содержащегося в элементарном объеме

.

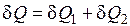Количество теплоты, поступающее к граням куба обозначим d Q_x,d Q_y,d Q_z, а количество теплоты, которое будет отводиться через противоположные грани в тех же направлениях, обозначим соответственно d Q_{x+ d x} ,d Q_{y+ d y} ,d Q_{z+ d z} . Учтем, что тепловой поток – это количество тепла, проходящее через единицу площади, перпендикулярной потоку. Тогда количество теплоты, проходящее через грань d y, d z в направлении оси х за время d τ равно

, (3.2)

где q_x – проекция теплового потока на нормаль к данной грани d y, d z.

Отведенное количество теплоты через противоположную грань в направлении оси х за время d τ равно

. (3.3)

В этом выражении функция q_{x +d x} на рассматриваемом интервале является непрерывной, поэтому разложим ее в ряд Тейлора:

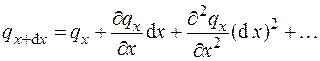. (3.4)

Ограничимся двумя членами разложения, тогда в направлении оси х количество теплоты равно

.

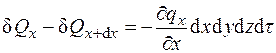Аналогичными выражениями определяется количество теплоты, проходящее через твердое тело в направлениях y и z. Общее количество теплоты, проходящее через рассматриваемый объем за время d τ, определяется по выражению

. (3.5)

Количество теплоты, поступившее в рассматриваемый объем горной породы, можно определить из первого начала термодинамики (1.13), но при переносе тепла работа не совершается, поэтому 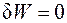, а количество теплоты

,

где с_m – удельная теплоемкость вещества; d m – масса вещества, заключенного в рассматриваемом объеме. Ее можно выразить следующим образом:

,

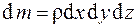где r – плотность вещества.

Подставляя выражение d m в количество теплоты, получаем

. (3.6)

Объединяя (3.5) и (3.6), получим

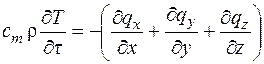. (3.7)

Принимая во внимание, что 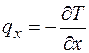, , , получим

. (3.8)

В операторной форме это выражение можно записать

, (3.9)

где Ñ – оператор набла; D – оператор Лапласа.

Выражения (3.8) или (3.9) представляют собой дифференциальное уравнение теплопроводности для трехмерного случая.

Коэффициент α называют коэффициентом температуропроводности. Он является мерой инерционных свойств тела в отношении выравнивания температуры, то есть чем больше коэффициент α, тем больше скорость изменения температуры в точках тела.

Если твердое тело или среда не содержат внутренних источников тепла, то дифференциальное уравнение теплопроводности имеет вид (3.8) или (3.9).

Для стационарного состояния, когда распределение тепла не изменяется с течением времени без внутренних источников тепла, дифференциальное уравнение теплопроводности принимает вид

. (3.10)

Но если при этом имеются внутренние источники тепла, то оно записывается так:

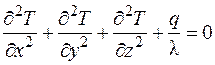. (3.11)

Дата добавления: 2015-05-26