Зависимость коэффициентов переноса разреженных газов от температуры

В курсе физики показано, что средняя длина свободного пробега молекул разреженного (идеального) газа определяется выражением

, (2.10)

где d – эффективный диаметр молекулы газа, м; n ₀ – концентрация молекул, м^–3.

При равновесном состоянии однородного газа вследствие хаотичного движения вероятность движения молекул в одном из направлений трехмерной системы координат равна 1/6.

При нарушении равномерной концентрации газа, то есть при возникновении локальных флуктуаций (максимумов и минимумов) концентрации возникает направленный перенос массы газа, определяемый законом Фика:

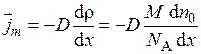, (2.11)

где 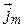– вектор плотности потока массы газа, имеющий обратное направление по сравнению с вектором градиента плотности, направленного в сторону быстрейшего увеличения, 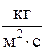; D – коэффициент диффузии, 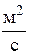; 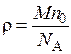– плотность газа, .

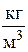Плотность потока массы газа 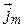– это масса газа, прошедшая через единичную площадку, перпендикулярную потоку, в единицу времени. Следовательно, масса газа, прошедшего через площадку d S за время d t по оси х, определяется выражением

. (2.12)

В рамках молекулярно-кинетической теории показано, что коэффициент диффузии определяется выражением

. (2.13)

Подставим в (2.13) выражение для средней длины свободного пробега молекул, то есть (2.10). Получим

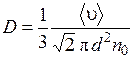. (2.14)

Средняя арифметическая скорость молекул определяется выражением

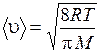. (2.15)

Подставляя (2.15) в (2.14), получаем

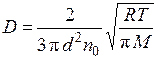. (2.16)

Из выражения (2.16) следует, что коэффициент диффузии прямо пропорционален 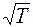. Учитывая, что концентрация также зависит от температуры:

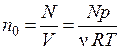, (2.17)

получаем, что коэффициент диффузии нелинейно зависит от температуры:

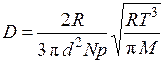. (2.18)

Поток газа характеризуется вязкостью. Рассмотрим, зависит ли от температуры динамический коэффициент вязкости (внутреннего трения), обусловленный обменом импульсами близлежащих слоев, движущихся с разными скоростями.

Величина коэффициента внутреннего трения определяется по формуле

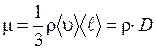. (2.19)

Данная формула может быть легко получена путем изменения импульса за счет перехода через площадку молекул слева и справа от рассматриваемой площадки. Нужно учесть, что изменение импульса со временем равно действующей силе, которая по отношению к одному слою является ускоряющей, а по отношению к другому – тормозящей. Если в выражение (2.19) подставить среднюю величину свободного пробега молекул и выражение для плотности из уравнения Клапейрона – Менделеева, то получим

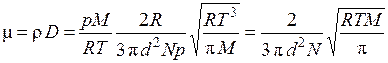. (2.20)

Следовательно, коэффициент вязкости в общем случае прямо пропорционален .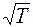

Рассмотрим процесс переноса тепловой энергии, который наблюдается в системе, в которой по какому-либо направлению имеется градиент температуры.

Перенос количества тепла в таком случае определяется законом Фурье, согласно которому через площадку d S за время d t по оси х проходит тепло:

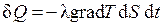. (2.21)

где l – коэффициент теплопроводности, .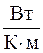

Величина коэффициента теплопроводности определяется выражением

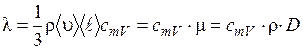. (2.22)

где с_mV – удельная теплоемкость при постоянном объеме.

Из выражения (2.22) видно, что коэффициент теплопроводности пропорционален коэффициенту вязкости, следовательно, коэффициент теплопроводности прямо пропорционален .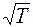

Представленные результаты расчета коэффициентов переноса по порядку величин согласуются с результатами измерений в широком диапазоне температур (от 250 до 850 К) и давлением от 5 до 500 кПа.

При достаточно низких или высоких давлениях расчетные величины коэффициентов переноса могут не соответствовать экспериментальным значениям по ряду причин. В частности, в формулах расчета длины свободного пробега (2.10) столкновение с другими движущимися молекулами учитывается посредством множителя , в действительности могут быть вероятными столкновения трех и более молекул. При достаточном вакууме средняя длина свободного пробега соизмерима с размерами сосуда. Таким образом, в формулах не учитывается взаимодействие молекул.

На основании уравнения Больцмана из статистической физики может быть получено обобщенное уравнение переноса, но к настоящему времени для него получены некоторые приближенные решения для частных случаев. Так англичанином Чепменом и шведом Энскогом получены следующие выражения:

, (2.23)

где d – диаметр молекул в ангстремах; 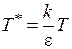– приведенная температура; e – глубина потенциальной ямы, Дж; р – давление, атм; W^(2.2) – интеграл столкновений;

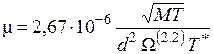; (2.24)

. (2.25)

Анализ формул (2.23) – (2.25), полученных из более обоснованных физических представлений, подтвердил, что коэффициент диффузии D пропорционален 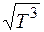, коэффициент вязкости μ пропорционален 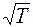и не зависит от давления.

При расчетах интегралы столкновений аппроксимируются некоторыми аналитическими выражениями от приведенной температуры. Отношение 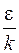примерно оценивают по температурам состояний:

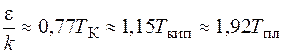. (2.26)

Дата добавления: 2015-05-26