Теплофизические свойства газов

Силы взаимодействия между молекулами разреженного газа являются дальнодействующими, их подразделяют на четыре типа: электростатические, дисперсионные, индукционные и резонансные.

Электростатические силы возникают между молекулами, обладающими дипольным моментом. Дипольным моментом не обладают атомы, находящиеся в S -состояниях, двухатомные молекулы, состоящие из одинаковых атомов, а также некоторые многоатомные молекулы, например, метан, диоксид углерода. Наличие зарядов разных знаков у диполей приводит к их определенной взаимной ориентации (эффект Кеезома), что несколько ограничивает свободу их перемещения.

Энергия электростатического взаимодействия описывается выражением

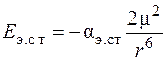, (2.1)

где 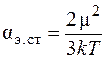– коэффициент поляризации; μ – дипольный момент молекул; k – постоянная Больцмана.

В большинстве случаев при количественном описании используют так называемые потенциалы межмолекулярного взаимодействия, знание которых позволяет легко рассчитать силы взаимодействия.

Одним из распространенных потенциалов межмолекулярного взаимодействия является потенциал Леннарда – Джонса:

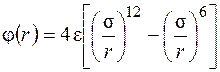, (2.2)

где e – минимальная энергия системы из двух молекул; s – минимальное расстояние между двумя молекулами.

Потенциал Леннарда – Джонса применяется для описания свойств газов, молекулы которых приближенно можно считать сферическими.

Для молекул, обладающих дипольным моментом, потенциал взаимодействия описывается выражением

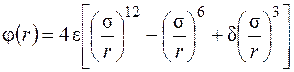, (2.3)

где d – функция угловой ориентации молекул.

Рассчитаем молярную теплоемкость разреженных многоатомных газов. Как известно, молярная теплоемкость при постоянном объеме рассчитывается по формуле (поскольку 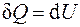в силу того, что при изохорном процессе работа равна нулю):

,

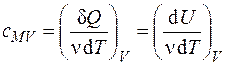где U – внутренняя энергия молекул, имеющая поступательную, вращательную и колебательную составляющие (другие составляющие слабо зависят от температуры, поэтому их не будем учитывать).

Энергия поступательного движения молекулы 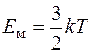, а суммарная энергия поступательного движения молекул одного моля газа равна: .

Тогда

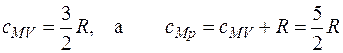. (2.4)

Энергия вращательного движения рассчитывается по известной формуле механики

,

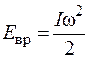где I – момент инерции относительно определенной оси; w – угловая скорость вращения относительно данной оси.

На одну степень свободы приходится энергия 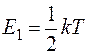. Тогда для линейных молекул О₂, N₂, H₂, так как вращение учитывается только около двух осей, поэтому энергия вращательного движения таких молекул составляет 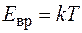. Молярная теплоемкость двухатомного газа равна:

.

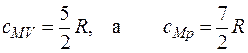Для газа, состоящего из нелинейных молекул с числом атомов N три и более:

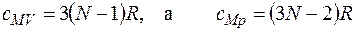. (2.5)

Составляющие энергии колебательного движения с учетом кинетической и потенциальной энергии и равномерного распределения энергии по степеням свободы .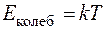

Анализ формул для расчета теплоемкости разреженного газа показывает, что теплоемкость не зависит от температуры. Но это справедливо только в определенном диапазоне температур. Дело в том, что почти для всех молекул приращение энергии по поступательным степеням свободы значительно меньше kT.

Для колебательных степеней свободы при малых температурах Т энергия квантов становится соизмеримой с kT, что нарушает допущение о равномерном распределении энергии по степеням свободы. В этой связи для нахождения теплоемкости многоатомных газов используют эмпирические методы расчета.

Метод Бенневица – Росснера – Добраца отличается от классических методов расчета тем, что учитывает вклад в энергию колебательных степеней свободы многоатомных молекул с учетом зависимости от температуры.

Пусть молекула имеет N атомов. Тогда у нее (3 N – K) степеней свободы (K – число связей), из которых три поступательные и три вращательные вокруг внешних осей. Оставшиеся (3 N – K – 6) степеней свободы распределяются между колебательными и внутренними вращательными степенями свободы. При этом колебания даже линейного осциллятора рассматриваются вдоль оси осциллятора и перпендикулярно ей в двух направлениях. Это так называемые «изгибающие» (поперечные) колебания. Каждая степень свободы обладает своей характеристической частотой.

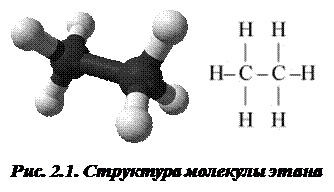Увеличение теплоемкости за счет внутреннего вращения составляет R /2 на моль для связи типа С–С, С–О, С–N в органических молекулах. Например, структуру молекулы этана можно представить таким образом, как показано на рис. 2.1.

Число внутренних вращательных степеней свободы отдельных частей молекулы относительно друг друга равно единице. Таким образом, в молекуле с N атомами (N – 1) растягивающих колебаний, а остальные являются изгибающими.

Энергетический вклад колебательных степеней свободы выражается формулой [2]

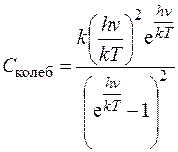. (2.6)

При высоких температурах выражение (2.6) стремится к k (на одну молекулу), а в расчете на моль – к R = kN_A.

С учетом дополнительных степеней свободы колебаний и внутренних вращений теплоемкость одного моля идеального газа, молекула которого содержит N атомов, можно выразить формулой

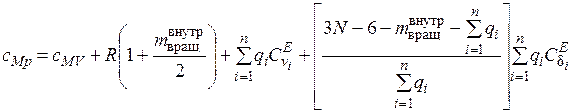,(2.7)

где – число внутренних вращательных степеней свободы;
с_МV = 3 R – вклад в теплоемкость поступательных и вращательных степеней свободы; – общее число валентных связей; – число изгибающих поперечных колебаний; 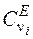, 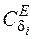– функции Эйнштейна, которые рассчитываются по формулам [2]:

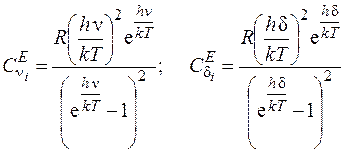, (2.8)

где ν, d – характеристические частоты растягивающих (продольных) и изгибающих (поперечных) колебаний.

Функции Эйнштейна аппроксимируются следующим полиномом:

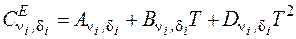, (2.9)

где – коэффициенты полинома. Значения коэффициентов для различных газов приведены в таблице.

Таблица 2.1

Коэффициенты полинома для функций Эйнштейна

Колебания	Растяжение – сжатие	Изгибные
связь	qi	A ν	B ν∙10^3	D ν∙10^6	A d	B d ∙ 10^3	D d ∙ 10^6
С–С		–1,09	6,0	–3,441	0,73	3,414	–2,577
С–Н		0,229	–1,224	1,658	–0,928	3,9	–1,342

При температурах порядка 300 К значения теплоемкости газов, рассчитанных данным методом, ниже экспериментальных, а при высоких температурах – превышают экспериментально измеренные. Данный метод нельзя использовать для соединений с тройными связями.

Пример. Рассчитаем удельную теплоемкость этилена С₂Н₄ при температуре 373 К.

Решение. Вначале найдем удельную теплоемкость при постоянном давлении по классической формуле (2.5):

.

Экспериментальное значение удельной теплоемкости при постоянном давлении составляет 1,53∙10³ 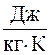. Расхождение результатов между экспериментальным значением и расчетным по классической формуле составляет порядка 200 %.

Рассчитаем удельную теплоемкость этилена С₂Н₄ методом Бенневица – Росснера – Добраца. Значения коэффициентов полинома (2.9) для колебаний растяжения – сжатия и изгибных колебаний связей С–С и С–Н возьмем из табл. 2.1.

Частота колебаний растяжения – сжатия для связей типа С–С составляет 2,97∙10¹³ Гц, а частота изгибных колебаний для этих связей равна 1,17∙10¹³ Гц. Аналогичные частоты для связей С–Н составляют 8,76∙10¹³ Гц и 3,96∙10¹³ Гц соответственно.

Далее по формуле (2.9) найдем функции Эйнштейна.

а) растяжения – сжатия для связей С–С

;

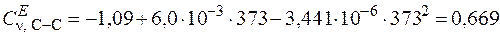б) изгибные для связей С–С

.

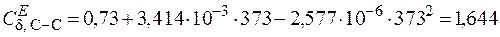Далее рассчитаем аналогичные функции Эйнштейна для связей С–Н:

;

.

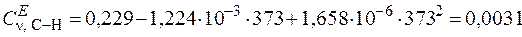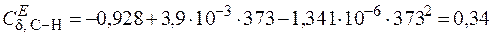Найдем сумму функций Эйнштейна для растягивающих и изгибающих колебаний по всем валентным связям:

;

.

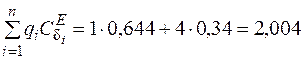Затем по формуле (2.7) определим молярную теплоемкость этилена

,

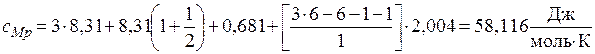а удельная теплоемкость будет равна

.

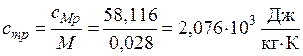Экспериментальное значение удельной теплоемкости при постоянном давлении составляет 1,53∙10³ 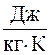. Расхождение результатов между экспериментальным значением и рассчитанным по методу Бенневица – Росснера – Добраца составляет не более 30 %.

Дата добавления: 2015-05-26