Третье начало термодинамики

Третье начало термодинамики играет значительную роль при описании процессов, протекающих при низких термодинамических температурах, то есть вблизи абсолютного нуля.

Нернст в 1906 г. на основании экспериментальных исследований систем при низких температурах установил, что по мере приближения температуры к 0 К энтропия всякой системы при изотермических равновесных процессах перестает зависеть от каких-либо термодинамических параметров и в пределе принимает одну и ту же постоянную величину, которую можно принять равной нулю.

Математически это можно записать следующим образом:

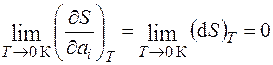, (1.26)

где a_i – любой термодинамический параметр системы.

Это положение и носит название третьего начала термодинамики.

С позиции статистического смысла энтропии при абсолютном нуле равновесному состоянию термодинамической системы соответствует одно макросостояние, термодинамическая вероятность которого равна единице (w = 1), следовательно, при Т = 0 К:

.

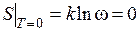С позиций статистической физики переход макроскопической системы к равновесию является не обязательным, но такой переход наиболее вероятен.

Существуют и другие формулировки третьего начала.

Применительно к обратимым изохорным процессам из первого начала термодинамики следует:

(W _max) _V = T (S ₂ – S ₁) – (U ₂ – U ₁). (1.27)

Поскольку термодинамический потенциал Гельмгольца (свободная энергия) равен:

F = U – TS, (1.28)

то получаем, что

(W _max) _V = F ₁ – F ₂,

то есть работа против немеханических сил совершается за счет убыли свободной энергии. Необходимо также учесть, что
(Q _max) _V = U ₁ – U ₂. Тогда с учетом этих положений получаем, что

.

Нернст обнаружил, что по мере приближения к абсолютному нулю:

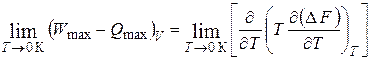. (1.29)

Здесь учтено, что из (1.28) следует:

.

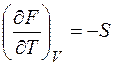Третье начало в формулировках Планка следует из аналогичных соотношений, полученных для изобарных процессов:

.

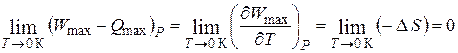Учтено, что в сложных системах убыль потенциала Гиббса равна работе против действующих на систему сил различной природы (механических и немеханических), то есть

(W _max) _P = Ф ₁ – Ф ₂, а (Q _max) _P = H ₁ – H ₂,

где Ф – потенциал Гиббса; Н – энтальпия.

Глава 2. Теплофизические свойства
веществ

Свойства газов, жидкостей и твердых тел в общем случае приведены в соответствующих справочниках. Но диапазон температур технологических процессов необычайно широк – от единиц градусов кельвина до нескольких тысяч. В этой связи справочники не могут обеспечить необходимой информацией о свойствах тел, участвующих в процессе, в таком диапазоне температур. Необходимо уметь хотя бы приближенно рассчитывать теплофизические свойства веществ по тем или иным данным.

Точные расчеты возможны только на основе молекулярно-кинетических представлений для идеальных газов или реальных, но сильно разреженных. Но в то же время путем расчета потенциалов молекулярного взаимодействия можно найти не только термодинамические равновесные характеристики, но и коэффициенты неравновесных процессов с допустимой погрешностью.

Дата добавления: 2015-05-26