Теплопередача через плоскую стенку

а) Пусть имеется плоская стенка толщиной d и коэффициентом теплопроводности l. На наружных поверхностях поддерживаются постоянными температуры Т ₁ и Т ₂. Ось О х направлена перпендикулярно стенке, естественно, что температура вдоль стенки остается постоянной. Дифференциальное уравнение стационарной теплопроводности для данного случая запишется следующим образом:

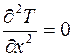. (3.13)

Граничные условия при этом следующие: при х = 0 Т = Т ₁, а при х = d Т = Т ₂.

После первого интегрирования получим

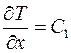. (3.14)

А после второго интегрирования получим

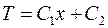. (3.15)

Постоянные найдем из граничных условий:

при х = 0, Т = Т ₁= С ₂, а при х = d, Т = Т ₂ = С ₁ d + T ₁. Откуда

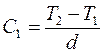. (3.16)

Следовательно, распределение температуры внутри стенки подчиняется линейному закону:

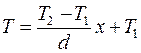, (3.17)

то есть линейно уменьшается от Т ₁ до Т ₂.

Величину 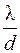называют тепловой проводимостью стенки, а обратную величину 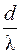– тепловым или термическим сопротивлением стенки. Количество теплоты, которое передается через поверхность стенки S за время τ, можно оценить по формуле

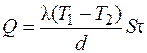. (3.18)

Плотность теплового потока при этом будет равна

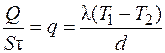. (3.19)

Если коэффициент теплопроводности зависит от температуры по близкому к линейному закону:

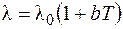, (3.20)

где l₀ – коэффициент теплопроводности при Т = 273 К;

b – постоянная.

Удельный тепловой поток на основании уравнения Фурье будет равен

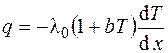. (3.21)

Тогда в любой точке внутри стенки с координатой х температура будет равна:

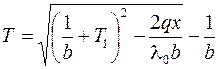. (3.22)

Из выражения (3.20) следует, что коэффициент теплопроводности стенки изменяется с ростом температуры по закону, близкому к линейному, а температура внутри стенки изменяется нелинейно с ростом х.

б) Пусть плоская стенка состоит из n слоев. Будем считать, что температура на поверхностях соприкасающихся слоев одинакова, а плотность потока не зависит от координаты х, то есть

q = const.

Тогда в соответствии с (3.19) будем иметь систему уравнений:

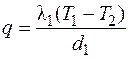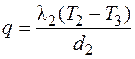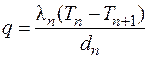; ; … . (3.23)

Сложив правые и левые части данных выражений, получим

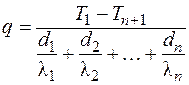. (3.24)

В выражении (3.24) сумму 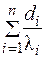называют полным термическим сопротивлением теплопроводности многослойной стенки. Внутри каждого слоя температура изменяется согласно (3.17), а внутри стенки представляет собой ломаную линию.

в) Передача тепла через стенку. Смысл данной задачи состоит в определении теплопередачи из одной подвижной среды в другую через одно- или многослойную стенку. Например, это теплопередача от горячей жидкости к холодной через стенку.

Для однослойной плоской стенки будем считать известными: толщину стенки d, коэффициент теплопроводности l, температуры Т ₁ (горячей жидкости) и Т ₂ (холодной жидкости), а также коэффициенты теплоотдачи l₁ и l₂, которые будем считать постоянными вдоль поверхностей стенки. Ось х направим также перпендикулярно стенке, а начало координат поместим в начало стенки. Задача ставится таким образом, что необходимо найти тепловой поток от горячей жидкости к холодной, а также определить температуру на самих поверхностях стенки. Воспользуемся уравнением (3.19) для определения плотности теплового потока от горячей жидкости к стенке 1 (х = 0):

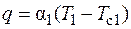, (3.25)

где Т _с1 – температура стенки при х = 0; α₁ – коэффициент теплопередачи этой стенки.

Эта же плотность теплового потока пройдет и через саму стенку, то есть

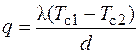, (3.26)

где Т _с2 – температура стенки при х = d.

К холодной жидкости пройдет плотность теплового потока

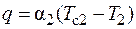. (3.27)

Учитывая, что в формулах (3.25) – (3.27) плотность теплового потока имеет одно и то же значение, можно, после несложных преобразований, получить

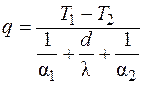. (3.28)

В выражении (3.28) величина 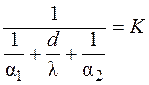, имеет размерность 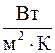и называется коэффициентом теплопередачи, который численно равен количеству теплоты, которое передается через единицу поверхности стенки от горячей жидкости к холодной в единицу времени при разности температур между горячей и холодной жидкостями в 1 К.

Если взять величину, обратную K, то получаем величину, называемую термическим сопротивлением теплопередачи:

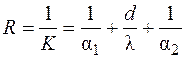. (3.29)

В случае многослойной стенки изменится только коэффициент теплопередачи, который будет рассчитываться по формуле

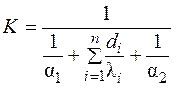. (3.30)

В соответствии с формулой (3.30) также изменится и выражение термического сопротивления.

Температуру стенок 1 и 2 можно найти по выражениям:

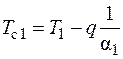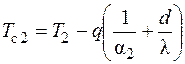; . (3.31)

А температура на границе любых двух слоев n и (n + 1) определяется выражением

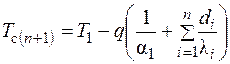. (3.32)

Дата добавления: 2015-05-26