Уравнение баланса

Суть уравнения баланса заключается в том, что изменение содержания массы вещества в определенном объеме пространства определяется потоком массы через поверхность, ограничивающую объем, и действием объемных источников. Математически это можно записать следующим образом:

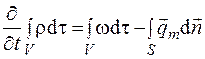, (4.5)

где r – функция объемной плотности; w – мощность объемного источника; 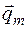– плотность потока массы (удельный поток).

По теореме Остроградского выразим поверхностный интеграл (4.5) через объемный. Будем иметь

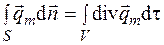. (4.6)

Выражение (4.6) подставим в (4.5), получим

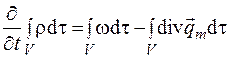. (4.7)

Если равны интегралы, то должны быть равны и подынтегральные выражения, т. е.

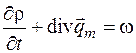. (4.8)

Первое слагаемое в этом выражении имеет смысл изменения функции объемной плотности вещества. Если речь идет о переносе энергии, то выражение (4.8) запишется следующим образом:

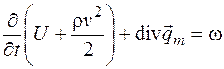, (4.9)

где U – внутренняя энергия единицы массы; 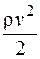– объемная плотность кинетической энергии, то есть .

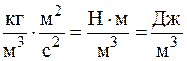Поскольку тепловой поток при конвективном переносе обеспечивается жидкостью, то плотность теплового потока при этом будем относить к единице массы жидкости, то есть

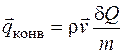, (4.10)

где 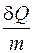– количество тепла, переносимое единицей массы жидкости.

Размерность выражения (4.10) 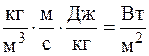, то есть совпадает с размерностью плотности теплового потока. Выражение 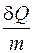в термодинамике носит название удельной энтальпии и обозначается .

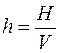Из дифференциального уравнения теплопроводности следует:

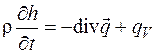, (4.11)

где 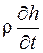имеет размерность 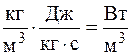, то есть мощность, приходящаяся на единицу объема. Она складывается из мощности потока переносимого тепла и мощности потока тепла внутренних источников.

Рассмотрим более подробно 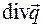. Оператор дивергенция преобразует вектор в скаляр

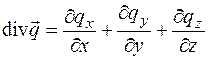, (4.12)

где плотности теплового потока по координатным осям вследствие теплопроводности и конвективного переноса определяются выражениями:

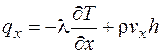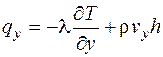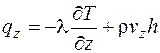; ; . (4.13)

Подставляя выражение (4.13) в (4.11), получим

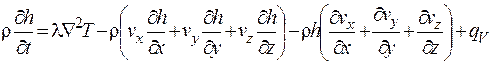. (4.14)

Выражение 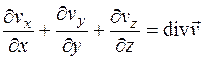, но для жидкостей r = const, то есть принимаем, что они являются несжимаемыми, поэтому 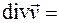0. Следовательно, из выражения (4.14) будем иметь

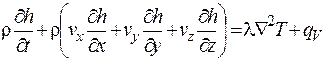. (4.15)

Учитывая, что полная производная от удельной энтальпии по времени равна сумме частной производной от удельной энтальпии по времени плюс сумма частных производных от удельной энтальпии по координатам x, y, z, умноженных на соответствующие проекции скорости переноса массы, получим

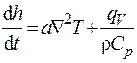, (4.16)

где 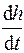– полная производная от удельной энтальпии по времени.

Выражение совместного переноса тепла за счет конвекции и теплопроводности в форме (4.16) наиболее общее, из него следуют частные случаи, когда перенос тепла не зависит от времени или происходит только по одной координате.

Дата добавления: 2015-05-26