Основные формулы и законы

Количество вещества тела (системы) – число структурных элементов (молекул, атомов, ионов и т.п.), содержащихся в телеили системе.

Количество вещества выражается в молях. Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде – 12 массой 0,012 кг.

Количество вещества тела (системы)

v = ,

где N – число структурных элементов (молекул, атомов, ионов и т.п.), составляющих тело (систему); N_A – по­стоянная Авогадро

(N_А = 6,02×10²³ моль^-1).

Молярная масса вещества

М = ,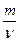

где m – масса однородного тела (системы); v – коли­чество вещества этого тела.

Относительная молекулярная масса вещества

,

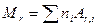где n_i – число атомов i -го химического элемента, входя­щих в состав молекулы данного вещества; A_r,i – относи­тельная атомная масса этого элемента. Относительные атомные массы приводятся в таблице Д.И. Менделеева. См. также в табл. А.10. прил. А. Связь молярной массы М с относительной молекуляр­ной массой вещества

М = ,

где k = 10^-3 кг/моль.

Количество вещества смеси газов

v = v₁+v₂+…+v_n = N₁/N_A + N₂/N_A +... +N_n/N_A,

или

,

где v_i, N_i, m_i, M_i – соответственно количество вещества, число молекул, масса, молярная масса i-го компонента смеси.

Уравнение Менделеева – Клапейрона (уравнение со­стояния идеального газа)

pV = 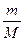RT = vRT,

где m – масса газа, М – молярная масса газа, R – мо­лярная газовая постоянная, v – количество вещества, Т – термодинамическая температура.

Опытные газовые законы, являющиеся частными слу­чаями уравнения Менделеева – Клапейрона для изопроцессов:

а) закон Бойля – Мариотта (изотермический процесс: T = const, m = const)

pV = const,

или для двух состояний газа

p₁V₁ = p₂V₂;

б) закон Гей-Люссака (изобарный процесс: р = const, m= const)

= const,

или для двух состояний газа

;

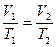в) закон Шарля (изохорный процесс: V = const, m = const)

= const,

или для двух состояний газа

;

г) объединенный газовый закон (m = const)

= const, или ,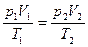

где p₁, V₁, T₁ – давление, объем и температура газа в начальном состоянии; p₂, V₂, T₂ – те же величины в ко­нечном состоянии.

Закон Дальтона, определяющий давление смеси газов

p= p₁+ p₂ +…+ p_n,

где p_i – парциальные давления компонентов смеси; п – число компонентов смеси.

Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.

Молярная масса смеси газов

,

где m_i – масса i- го компонента смеси; – количество вещества i -го компонента смеси; п – число ком­понентов смеси.

Массовая доля i -го компонента смеси газа (в долях единицы или процентах)

,

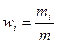где m – масса смеси.

Концентрация молекул

,

где N – число молекул, содержащихся в данной системе; ρ – плотность вещества; V – объем системы. Формула справедлива не только для газов, но и для любого агре­гатного состояния вещества.

Основное уравнение кинетической теории газов

,

где – средняя кинетическая энергия поступательного движения молекулы.

Средняя кинетическая энергия поступательного движения молекулы

,

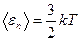где k – постоянная Больцмана.

Средняя полная кинетическая энергия молекулы

,

где i – число степеней свободы молекулы.

Зависимость давления газа от концентрации молекул и температуры

р = nkT.

Среднее число столкновений, испытываемых одной молекулой газа за 1 с

,

где d – эффективный диаметр молекулы; n – концентрация молекул; – средняя арифметическая скорость молекул газа.

Средняя длина свободного пробега молекул газа

,

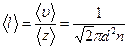где – средняя арифметическая скорость молекул газа;

– среднее число столкновений, испытываемых одной молекулой газа за 1 с;

d – эффективный диаметр молекулы;

n – концентрация молекул.

Масса m газа, перенесенная за время t через поверхность площадью S в результате диффузии, определяется законом Фика

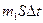, или ,

где D – коэффициент диффузии; – градиент концентрации молекул; m₁ – масса одной молекулы; – градиент плотности газа.

Коэффициент диффузии

,

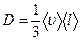где – средняя арифметическая скорость; 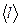– средняя длина свободного пробега молекул газа.

Сила F внутреннего трения между движущимися слоями газа определяется законом Ньютона

,

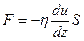где 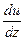– градиент скорости течения газа в направлении, перпендикулярном к поверхности площадью S; 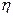– коэффициент внутреннего трения (динамическая вязкость).

Коэффициент внутреннего трения (динамическая вязкость)

,

где – средняя арифметическая скорость; 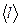– средняя длина свободного пробега молекул газа; 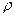– плотность газа.

Количество тепла Q, перенесенное за время 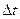через поверхность площадью S в результате теплопроводности определяется законом Фурье

,

где 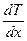– градиент температуры; – коэффициент теплопроводности.

Коэффициент теплопроводности

,

где – средняя арифметическая скорость; 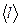– средняя длина свободного пробега молекул газа; 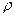– плотность газа; с_V – удельная теплоемкость газа при постоянном объеме.

Удельные теплоемкости газа при постоянном объеме (с_V) и постоянном давлении (с_р)

, .

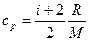Связь между удельной с и молярной С теплоемкостями

с = , С = сМ.

Уравнение Майера

C_p – C_V = R.

Внутренняя энергия идеального газа

.

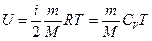Первое начало термодинамики

Q = ΔU + A,

где Q – теплота, сообщенная системе (газу); ΔU – из­менение внутренней энергии системы; А – работа, совер­шенная системой против внешних сил.

Работа расширения газа: в общем случае;

A = 0 при изохорном процессе, т.к. V = const;

A = p(V₂ – V₁) при изобарном процессе;

А = при изотермическом процессе;

A = -ΔU = - 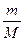C_VΔT, или A = при адиабатном процессе, где γ = – показатель адиабаты.

Уравнения Пуассона, связывающие параметры иде­ального газа при адиабатном процессе:

pV^γ = const, ,

, .

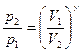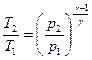Термический коэффициент полезного действия (КПД) цикла

,

где Q₁ – теплота, полученная рабочим телом от теплоотдатчика;

Q₂ – теплота, переданная рабочим телом теплоприемнику.

Термический КПД цикла Карно

,

где Т₁ и T₂ – термодинамические температуры теплоотдатчика и теплоприемника.

Закон Стефана-Больцмана

R_e = σT⁴,

где R_e – энергетическая светимость (излучательность) абсолютно черного тела; σ – постоянная Стефана-Больцмана; Т – термодинамическая температура Кельвина.

Закон смещения Вина

λ_m = b/T,

где λ_m – длина волны, на которую приходится максимум энергии излучения; b – постоянная Вина.

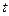Количество теплоты, проходящее через изотермическую поверхность в единицу времени называется тепловым потоком – , [Вт=Дж/с]. Тепловой поток, проходящий через единицу площади

называют плотностью теплового потока – [Вт/м²].

Стационарная теплопроводность через плоскую стенку

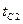Рассмотрим однородную плоскую стенку толщиной (рис.), на наружных поверхностях которой поддерживаются постоянные температуры и . Коэффициент теплопроводности стенки постоянен и равен . В стационарном режиме 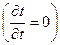и отсутствии внутренних источников теплоты () дифференциальное уравнение теплопроводности примет вид:

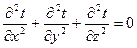
При заданных условиях температура изменяться только в направлении оси 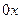, перпендикулярном плоскости стенки. В этом случае

и уравнение теплопроводности запишется в виде: . Запишем граничные условия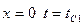: при ; при .

Плотность теплового потока вычисляется по формуле

,

а уравнение температурной кривой имеет вид:

Дата добавления: 2015-05-26