Примеры решения задач. Пример 1. В баллоне объемом 10 л находится гелий под давлением p1 = 1 МПа и при температуре Т1 = 300 К

Пример 1. В баллоне объемом 10 л находится гелий под давлением p₁ = 1 МПа и при температуре Т₁ = 300 К. После того как из баллона было взято m = 10 г гелия, температура в нем понизилась до T₂ = 290 К. Опре­делить давление р₂ гелия, оставшегося в баллоне.

Решение. Для решения задачи воспользуемся уравнением Менделеева–Клапейрона, применив его к конечному состоянию газа:

p₂V = 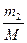RT₂, (1)

где m₃ – масса гелия в баллоне в конечном состоянии; М – молярная масса гелия; R – молярная газовая по­стоянная.

Из уравнения (1) выразим искомое давление

p₂ = m₂RT₂/(MV). (2)

Массу т₂ гелия выразим через массу т₁, соответству­ющую начальному состоянию, и массу m гелия, взятого из баллона

m₂ = m₁ - m. (3)

Массу m₁ гелия найдем также из уравнения Менде­леева – Клапейрона, применив его к начальному со­стоянию:

m₁ = Mp₁V/(RT₁). (4)

Подставив выражение массы т₁ в (3), а затем выра­жение т₂ в (1), найдем

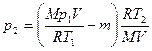, или . (5)

Проверим, дает ли формула (5) единицу давления. Для этого в ее правую часть вместо символов величин подставим их единицы. В правой части формулы два слагаемых. Очевидно, что первое из них дает единицу давления, так как состоит из двух множителей, первый из которых (T₂/T₁) – безразмерный, а второй – давле­ние. Проверим второе слагаемое:

.

Паскаль является единицей давления. Произведем вычисления по формуле (5), учитывая, что М= 4×10^-3 кг/моль:

= 3,64×10⁵ Па = 0,364 МПа.

Пример 2. Баллон содержит m₁ = 80 г кислорода и m₂ = 320 г аргона. Давление смеси р= 1 МПа, температу­ра Т = 300 К. Принимая данные газы за идеальные, определить объем V баллона.

Решение. По закону Дальтона, давление смеси равно сумме парциальных давлений газов, входящих в состав смеси. По уравнению Менделеева – Клапейрона, парциальные давления р₁ кислорода и р₂ аргона выра­жаются формулами

p₁ = m₁RT/(M₁V), p₂ = m₂RT/(M₂V).

Следовательно, по закону Дальтона, давление смеси газов

p= p₁+ p₂, или ,

откуда объем баллона

.

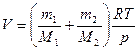Произведем вычисления, учитывая, что M₁ = 32×10^-3 кг/моль,

M₂ = 40×10^-3 кг/моль (см. табл. А.10 прил. А):

= 0,0262 м³ = 26,2 л.

Пример 3 При каком давлении р средняя длина свободного пробега á l ñ молекул азота равна 1 м, если температура газа t ° = 100 °С?

Решение. Давление газа определим как p = nkT, а концентрацию газа определим, используя формулу средней длины свободного пробега молекул 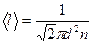. Откуда .

Произведем вычисления, для чего вычислим температуру азота Т=273+100=373 К, постоянная Больцмана k=1,38×10^-23 Дж/К (см. табл. А.1 прил. А). Значение эффективного диаметра d молекулы азота определим, воспользовавшись табл. А.7. прил. А, d =3×10^-10 м:

12, 9×10^-3 Па = 12,9 мПа .

Пример 4. Средняя длина свободного пробега 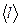атомов гелия при нормальных условиях равна 180 нм. Определить коэффициент диффузии D гелия.

Решение. Коэффициент диффузии D определяется формулой

,

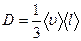где – средняя арифметическая скорость молекул газа;

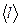– средняя длина свободного пробега молекул.

Средняя арифметическая скорость молекул определяется по формуле

,

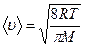где R – молярная газовая постоянная; М – молярная масса газа.

Для нормальных условий Т = 273 К, тогда получим

.

Гелий – газ одноатомный, используя табл. А.10 прил. А, определим молярную массу гелия М = 4×10^-3 кг/моль.

Произведем вычисления:

= 7,23×10^-5 м²/c.

Пример 5. Вычислить удельные теплоемкости при постоянном объеме с_V и при постоянном давлении c_p неона и водорода, принимая эти газы за идеальные.

Решение. Удельные теплоемкости идеальных газов выражаются формулами

, ,

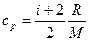где I – число степеней свободы молекулы газа; М – мо­лярная масса. Для неона (одноатомный газ) i = 3 и М = 20×10^-3 кг/моль. Произведем вычисления:

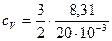= 2,64×10² Дж/(кг×К);

= 1,04×10³ Дж/(кг×К).

Для водорода (двухатомный газ) i = 5 и М = 2×10^-3 кг/моль. Тогда = 1,04×10⁴Дж/(кг×К);

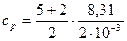= 1,46×10³Дж/(кг×К).

Пример 6. Вычислить удельные теплоемкости c_V и c_р смеси неона и водорода, если массовые доли неона и водорода составляют

w₁ = 80 % и w₂ = 20 %. Значения удельных теплоемкостей газов взять из предыдущего примера.

Решение. Удельную теплоемкость с_V смеси при постоянном объеме найдем следующим образом. Теплоту, необходимую для нагревания смеси на ΔT, выразим двумя способами:

Q = с_V(m₁ + m₂)ΔT; (2.19)

Q = (с_V,1m₁+ с_V,2m₂)ΔT, (2.20)

где c_V,1 – удельная теплоемкость неона; c_V,2 – удельная теплоемкость водорода.

Приравняв правые части (2.19) и (2.20) и разделив обе части полученного равенства на ΔT, получим c_V(m₁ + m₂) = с_V,1m₁+ с_V,2m₂.

Отсюда

,

или

c_V= c_V,1w₁+ c_V,2w₂,

где и .

Рассуждая так же, получим формулу для вычисления удельной теплоемкости смеси при постоянном давлении:

c_p=c_p,1w₁+c_p,2w₂.

Произведем вычисления:

c_V = (6,24×10²×8 +1,04×10⁴×0,2) = 2,58×10³ Дж/(кг×К) =

= 2,58 кДж/(кг×К);

c_p = (1,04×10³× 0,8+1,46×10⁴×0,2) = 3,75×10³Дж/(кг×К)=

= 3,75 кДж/(кг×К).

Пример 7. Кислород массой m = 2 кг занимает объем V₁ = 1м³ и находится под давлением р₁ = 0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V₂ = 3 м³, а затем при постоянном объеме до давления р₃ = 0,5 МПа. Найти изменение ΔU внутренней энергии газа, совершенную им работу А и теплоту Q, передан­ную газу. Построить график процесса.

Решение. Построим график процесса в координатных осях p-V.

Так как сначала газ изобарно расширялся, то этому про-цессу соответствует на гра-фике отрезок 1-2 (рис.). Затем газ был изохорно нагрет, что приводит к увели-чению давления; этому про-цессу соответствует на гра-фике отрезок 2-3 (рис. 2.1).

Определение требуемых физических величин можно осуществить двумя вариантами.

Первый вариант. Изменение внутренней энергии газа

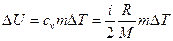, (1)

где i – число степеней свободы молекул газа (для двух­атомных молекул кислорода i=5); ΔT = Т₃ - Т₁ – раз­ность температур газа в конечном (третьем) и начальном состояниях.

Начальную и конечную температуру газа найдем из уравнения Менделеева – Клапейрона pV = 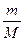RT, откуда

.

Работа расширения газа при постоянном давлении выражается формулой

.

Работа газа, нагреваемого при постоянном объеме, равна нулю:

А₂ = 0.

Следовательно, полная работа, совершаемая газом:

А = А₁ + А₂ = А₁.

Согласно первому началу термодинамики, теплота Q, переданная газу, равна сумме изменения внутренней энергии ΔU и работы А:

Q = ΔU + А.

Произведем вычисления, учитывая, что для кислорода М = 32×10^-3 кг/моль:

К;

К;

К;

;

A=A₁=0,4 МДж;

;

Q = (3,24 + 0,4) МДж = 3,64 МДж.

Второй вариант. Воспользуемся графиком на рис. 2.1, тогда для участка 1-2 запишем первое начало термодинамики Q₁ = Δ U₁ + А₁.

Для изобарного процесса: А₁ = р₁ (V₂ - V₁), Δ U₁ = .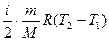

Воспользуемся уравнением Менделеева-Клапейрона для состояний 1 и 2 (на графике точки 1 и 2 соответственно):

; (2)

. (3)

Так как р₁ = р₂, то вычтя из уравнения (3) уравнение (2), получим

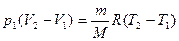, тогда Δ U₁ = А₁, Q₁ = А₁( + 1).

Для участка 2-3: Q₂ = Δ U₂ + А₂. Этот участок соответствует изохорному процессу, значит А₂ = 0, Δ U₂ = .

Воспользуемся уравнением Менделеева-Клапейрона для состояния 3 (на графике точка 3):

. (4)

Вычтем из уравнения (4) уравнение (3), получим

. Из графика видно, что р₁ = р₂, а V₂ = V₃,

откуда 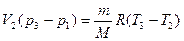, тогда Δ U₂ = V₂(p₃ – p₁), Q₂ = Δ U₂.

Тогда А = А₁, Δ U = Δ U₁ + Δ U₂, Q = Q₁ + Q₂.

Произведем вычисления:

А = 0,2×10⁶(3 – 1)= 0,4×10⁶ Дж = 0,4 МДж;

Δ U = 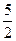×0,4×10⁶ + 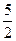×3×10⁶(0,5 – 0,2) = 3,25×10⁶ Дж = 3,25 МДж;

Q = 0,4×10⁶ + 3,25×10⁶ = 3,65×10⁶ Дж = 3,65 МДж.

Пример 8. В цилиндре под поршнем находится водо­род массой т = 0,02 кг при температуре T₁ = 300 К. Водород сначала расширился адиабатно, увеличив свой объем в n₁ = 5 раз, а затем был сжат изотер­мически, причем объем газа умень­шился в n₂ = 5 раз. Найти темпера­туру в конце адиабатного расшире­ния и работу, совершаемую газом при этих процессах. Изобразить процесс графически.

Решение. Температуры и объемы газа, совершающего адиабатный процесс, связаны между собой соотношением

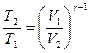, или ,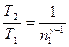

где γ – отношение теплоемкостей газа при постоянном давлении и постоянном объеме; n₁ = .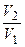

Отсюда получаем следующее выражение для конечной температуры:

.

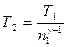Работа А₁ газа при адиабатном расширении может быть определена по формуле

,

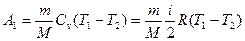где C_V – молярная теплоемкость газа при постоянном объеме. Работа A₂ газа при изотермическом процессе может быть выражена в виде

, или ,

где n₂ = .

Произведем вычисления, учитывая, что для водорода, как двухатомного газа: γ = 1,4; i = 5 и М = 2×10^-3 кг/моль:

;

;

.

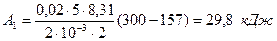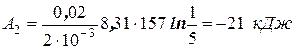Знак минус показывает, что при сжатии работа газа совершается над газом вне­шними силами. График процесса приве­ден на рис.

Пример 9. Тепловая ма­шина работает по обратимо­му циклу Карно. Температу­ра теплоотдатчика Т = 500 К. Определить термический КПД η цикла и температуру Т₂ теплоприемника тепловой машины, если за счет каждого кило­джоуля теплоты, полученной от теплоотдатчика, машина совершает работу А = 350 Дж.

Решение. Термический КПД тепловой машины показывает, какая доля теплоты, полученной от теплоотдатчика, превращается в

механическую работу. Терми­ческий КПД выражается формулой

,

где Q₁ – теплота, полученная от теплоотдатчика; А – работа, совершенная рабочим телом тепловой машины. Зная КПД цикла, можно по формуле 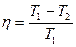определить температуру охладителя T₂:

T₂=T₁ (1 - η).

Произведем вычисления:

η = 350/1000 = 0,35; Т₂ = 500(1- 0,35) К = 325 К.

Пример 10. Длина волны, на которую приходится максимум энергии в спектре излучения черного тела, λ₀ = 0,58 мкм. Определить энергетическую светимость (излучательность) R_e поверхности тела.

Решение. Энергетическая светимость R_e абсолютно черного тела в соответствии с законом Стефана-Больцмана пропорциональна четвертой степени термодинамической температуры и выражается формулой

R_e=σT⁴, (1)

где σ – постоянная Стефана-Больцмана; Т – термодинамическая температура.

Температуру Т можно вычислить с помощью закона смещения Вина:

λ₀ = b / Т, (2)

где b – постоянная закона смещения Вина.

Используя формулы (1) и (2), получаем

.

Произведем вычисления:

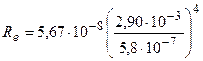= 3,54·10⁷ Вт/м² = 35,4 МВт/м².

Пример 11. В модели абсолютно черного тела (см. рис.) температура стенок полости поддерживается равной 2000 К. Площадь отверстия S = 1 мм². Определить энергию, излучаемую через отверстие за 1 мин.

Решение. Воспользовавшись законом Стефана-Больцмана, находим искомую величину

Е = R·St = σT⁴St,

где, по условию, Т = 2000 К, t = 60 с, S = 10^{-6 м2}.

Произведя вычисления, получим ответ: Е = 54,4 Дж.

Пример 12. Максимум излучательной способности поверхности Солнца приходится на длину волны λ_max =0,5 мкм.

1) Определить температуру солнечной поверхности, считая, что она по своим свойствам близка к абсолютно черному телу.

2) Найти значение солнечной постоянной – интенсивности солнечного излучения вблизи Земли, за пределами ее атмосферы.

Решение.

1) Температуру солнечной поверхности определим с помощью закона Вина

T = b/ λ_max.

Произведя вычисления, получим Т = 5800 К.

2) Значение солнечной постоянной С находим, разделив поток энергии Ф_E, излучаемый Солнцем по всем направлениям, на площадь поверхности сферы, радиус которой равен среднему расстоянию от Земли до Солнца L = 1,5*10¹¹м(рис. 6.3).

Поток энергии Ф_E равен произведению энергетической светимости R^* Солнца на площадь его поверхности, т.е. Ф_E =R·4πr_c², где r_c ≈ 7*10⁸м – радиус Солнца. Тогда

.

Произведя вычисления, получим ответ:

C = 1400 Дж/(м²с), Т = 5800 К.

Пример 13. Каково значение коэффициента теплопроводности материала стенки, если и тепловые потери

Дата добавления: 2015-05-26