Приклад 5

На внесок у банк у розмірі 8500 грн строком на шість років нарахо­вується 15 % річних за схемою складних відсотків. Яка сума буде на рахунку в кінці означеного періоду, якщо нарахування відсотків здійс­нюється щокварталу?

Розрахунок буде таким:

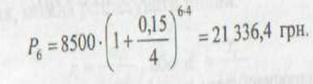
Використання в розрахунках складних відсотків у разі багато­разового його нарахування більш логічно, оскільки в цьому ви­падку капітал, що генерує доходи, постійно зростає. При застосу­ванні простого відсотка доходи в міру їх нарахування доцільно знімати для споживання або використання в інших інвестиційних проектах чи поточній діяльності.

Формула складних відсотків є однією з базових формул у фі­нансових розрахунках, тому для зручності користування значен­ня множника FМ1{r, n),що називається мультиплікатором і за­безпечує нарощення вартості, табульовані для різних значень r і п. Тоді формула алгоритму нарощення за схемою складних відсот­ків матиме такий вигляд:

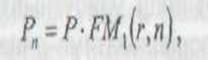
де FM1 (r,n) = (1+r) —мультиплікатор

Економічний зміст множника FM1 (r,n) полягає в тому, що він показує, чому буде дорівнювати одна грошова одиниця через п періодів при заданій відсотковій ставці r.

У практичних розрахунках для наочної та швидкої оцінки ефективності запропонованої ставки нарощення при реалізації схеми складних відсотків користуються приблизним розрахун­ком часу, необхідного для подвоєння інвестиційної суми, відомо­го як «правило 72-х». Це правило передбачає, що якщо r — від­соткова ставка, то к = 72/r являє собою кількість періодів, за яке вихідна сума збільшиться приблизно вдвічі.

Таке правило добре спрацьовує для невеликих значень r (до 20%). Так, якщо річна ставка r- 12 %, то к~ 72 /12 = 6.

Оцінюючи доцільність фінансових вкладень у той чи інший вид бізнесу, виходять з того, що визначають прибутковість цих вкладень. Завдання зводиться до того, щоб порівняти інвестиції, які підприємець має зробити сьогодні, із грошових надходжень, які він отримає в майбутньому. Тобто виникає необхідність порів­няння сум грошей у різні моменти часу. Для цього їх приводять до одного часового знаменника — до теперішнього часу.

Основна ідея цієї процедури полягає в тому, щоб оцінити майбутні грошові надходження з позиції поточного моменту, тобто визначити величину суми Р, яка в майбутньому має стано­вити задану величину Р_п. У цьому випадку Р буде відповідати поточній (теперішній, приведеній) вартості Р_п.

Теперішня вартість — грошова вартість майбутніх доходів на теперішній час. Розрахунки теперішньої вартості здійснюють іа допомогою дисконтування.

Дисконтування — це зведення економічних показників різ­них років до порівняльного в часі виду. Дисконтування здійсню­ють за допомогою формули

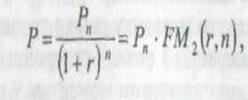
де Рn — майбутня вартість; Р — поточна вартість; 1 / (1 + r)ⁿ — коефіцієнт дисконтування.

Значення коефіцієнта дисконтування табульовані, а його еко­номічний зміст полягає в тому, що він відображує теперішню ці­ну однієї грошової одиниці майбутнього, тобто чому з позиції поточного моменту дорівнюватиме одна грошова одиниця, що циркулює у сфері бізнесу п періодів з моменту розрахунку при заданій відсотковій ставці г та частоті нарахування відсотків.

Дата добавления: 2015-05-26