Электронная оболочка атома

Химические свойства элемента определяются строением электронной оболочки атома. При рассмотрении строения электронной оболочки атома необходимо учитывать, что из-за корпускулярно-волновой природы электрона существует неопределённость в установлении его места пребывания. Эрвин Шредингер предложил волновое уравнение для описания состояния электрона в атоме:

▼² ψ + 8π²m/h · (E – U) ·ψ = 0.

В уравнение Шредингера входит волновая функция Ψ. Квадрат её модуля / ψ²/ является мерой вероятности нахождения электрона в некотором объеме на определенном расстоянии от ядра. Решение этого уравнения даёт плотность вероятности нахождения электрона в данной области пространства. Область пространства вокруг ядра, для которой вероятность пребывания электрона равна 95%, называется атомнойорбиталью. Электрон не вращается по орбите, а занимает трёхмерную область в пространстве вокруг ядра – орбиталь. Налагаемые на функцию Ψ ограничения приводят к тому, что решения волнового уравнения Шредингера содержат целочисленные значения, называемые квантовыми числами (n, L, m, S).

Квантовые числа характеризуют состояние электрона в атоме (орбиталь электрона).

n – главное квантовое число. Определяет энергетический уровень, на котором находится электрон (орбиталь электрона). Определяет энергию электрона на уровне и размер орбитали. Может принимать значения

n = 1,2,3,4,5,6,7…∞.

В зависимости от значения главного квантового числа электрон может находится на 1, 2, 3 и т.д. энергетическом уровне. Чем больше значение главного квантового числа, тем больше энергия электрона и больше размер орбитали.

L - орбитальное квантовое число. Определяет энергетический подуровень, на котором находится электрон (орбиталь электрона). Определяет энергию электрона на подуровне, а также форму орбитали. Может принимать целочисленные значения

L = от 0 до (n-1).

Например. Четвертый энергетический уровень (n=4) в электронной оболочке содержит четыре подуровня, определяемые значениями орбитального квантового числа L = 0,1,2,3.

Подуровни обозначают латинскими буквами, чтобы не спутать с обозначением главного квантового числа:

L = 0 обозначают s; электрон находится на s подуровне;

L = 1 (p) – электрон находится на p подуровне;

L = 2 (d) – электрон находится на d подуровне;

L = 3 (f) – электрон находится на f подуровне и т.д.

Состояние электрона, характеризуемое значениями n и L, записывается электронной формулой.

Например,электрон находится на 4 энергетическом уровне (n = 4) и подуровне, характеризуемым L = 3. Состояние электрона, можно записать электронной формулой 4f.

Из взаимосвязи главного и орбитального квантовых чисел можно определить возможное число подуровней на энергетическом уровне:

I энергетический уровень (n = 1, L = 0) содержит 1 подуровень. Электронная формула электронов на I уровне 1s;,

II энергетический уровень (n = 2, L = 0, 1) содержит 2 подуровня. Электронная формула электронов на II уровне 2s2p;

III энергетический уровень (n = 3, L = 0, 1, 2) содержит 3 подуровня. Электронная формула электронов на III уровне 3s3p3d;

IV энергетический уровень (n = 4, L = 0, 1, 2,3) содержит 4 подуровня. Электронная формула электронов на IV уровне 4s4p4d4f и т.д.

В пределах одного энергетического уровня наименьшей энергией обладают электроны на s-подуровне (s-электроны). Повышение энергии по подуровням происходит в последовательности:

s < p < d < f < и.т.д.

Орбиталь электрона на s-подуровне (s-электроны) имеет сферическую форму, орбиталь p-электрона - симметричную гантель, у других (d-, f-электроны) орбитали имеют более сложную конфигурацию.

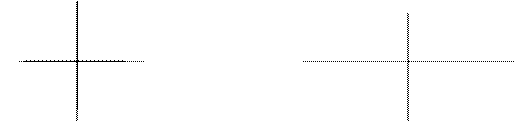
а в

Рис. 1 Формы орбиталей s –электрона (a) и p – электрона (в)

m - магнитное квантовое число. Определяет возможное число орбиталей на подуровне, а также пространственное расположение орбиталей. Может принимать значение целых чисел от + L до – L, включая нуль (+L…0…-L).

Возможное число орбиталей для подуровней:

L = 0(s) m = 0 одна s-орбиталь,

L = 1(p) m = 1,0,-1 три p-орбитали,

L = 2(d) m = 2,1,0,-1,-2 пять d-орбиталей,

L = 3(f) m = 3,2,1,0,-1,-2,-3 семь f-орбиталей и т. д.

Для р-орбиталей ось гантели расположена по осям X,Y,Z.

S -спиновое квантовое число. Определяет вращение электрона вокруг собственной оси. Это вращение по часовой стрелке или против неё. Может принимать значения +1/2 или –1/2.

Строение многоэлектронных атомов

Согласно решениям волнового уравнения Шредингера (квантовым числам) в многоэлектронных атомах электроны располагаются по энергетическим уровням (n), подуровням (L) и орбиталям (m). Если орбиталь обозначим в виде ячейки,

то структуру электронной оболочки можно изобразить электронной схемой:

1 энергетический уровень: 1

s

2 энергетический уровень: 2 p

s

3 энергетический уровень: 3 p d

s

4 энергетический уровень: 4 p d f

s и т.д.

Рассмотрим последовательность заполнения электронами полученной структуры электронной оболочки.

В соответствии с принципом Паули «в атоме не может быть двух электронов, обладающих одинаковым набором четырёх квантовых чисел». Отсюда следует, что на одной орбитали максимально может находиться только два электрона с противоположными спинами:

на 1 энергетическом уровне находится 2 электрона 1s²;

на 2 энергетическом уровне находится 8 электронов 2s²2р⁶;

на 3 энергетическом уровне находится 18 электронов 3s²3р⁶3d¹⁰;

на 4 энергетическом уровне находится 32 электрона 4s²4р⁶4d¹⁰4f¹⁴ и т.д.

Заполнение электронной оболочки атома происходит по принципунаименьшей энергии: «Электроны в основном состоянии заполняют орбитали в порядке повышения уровня энергии орбиталей».

Энергия состояния электрона (орбитали электрона) определяется энергией уровня и подуровня. Для определения порядка заполнения электронной оболочки используют правило В. Клечковского.

«Увеличение энергии и заполнение орбиталей происходит в порядке возрастания суммы главного и орбитального квантовых чисел (n +L). При равных значениях суммы (n+L) заполняется орбиталь с меньшим значением главного квантового числа».

Например, определить порядок заполнения электронами состояний, характеризуемых электронными формулами 5d, 6p, 6s.

5d = 5 + 2 = 7; 6p = 6 + 1 = 7; 6s = 6 + 0 = 6.

Порядок заполнения 6s,5d,6р.

Заполнение орбиталей внутри одного подуровня происходит по правилу Хунда:

«Каждая орбиталь заполняется вначале одним электроном, а затем происходит их заполнение вторым электроном».

Например, на 4p–подуровне 3 электрона (4p³) располагаются:

4

р

Таким образом, построенная согласно квантовым числам, структура электронной оболочки

1s

2s 2p

3s 3p 3d

4s 4p 4d 4f

5s 5p 5d 5f 5g

6s 6p 6d 6f 6g 6h и т.д.

будет заполняться согласно принципу наименьшей энергии (правилу Клечковского) для атома, например элемента свинца в следующей последовательности

₈₂Pb 1s²

2s²2p⁶

3s²3p⁶

4s²3d¹⁰4p⁶

5s²4d¹⁰5p⁶

6s²4f¹⁴5d¹⁰6p²

Электронные оболочки атомов элементов записываются в виде электронных формул:

₈₂Pb 1s²2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁶5s²4d¹⁰5p⁶6s²4f¹⁴5d¹⁰6p²

Дата добавления: 2015-05-26