Принятие оптимальных решений в экономике 1 страница

Нижегородский государственный

технический университет

Кафедра Экономики и Предпринимательства

Методические указания к выполнению курсовой работы

Нижний Новгород 2010.

для студентов социально-экономического факультета

Составители: Ф.Ф. Юрлов, М.Ю. Маркитанов, А.Ф. Плеханова

УДК 339.977

ББК 65.011

Принятие оптимальных решений в экономике: Метод. рекомендации к выполнению курсовой работы для студентов социально-экономического факультета НГТУ/ НГТУ; Сост.: Ф.Ф. Юрлов и др. Н.Новгород, 2010. С. 53

Рассмотрены методы принятия оптимальных решений при наличии неуправляемых факторов с учетом нескольких критериев. Предназначены для студентов социально-экономического факультета НГТУ. Могут быть использованы аспирантами, научными работниками и преподавателями экономических дисциплин вузов.

Рецензент: Ю.В.Трифонов

Редактор И.И. Морозова

Подп. к печ. 18.01.01. Формат 60х84¹/16. Бумага газетная. Печать

офсетная. Печ.л. Уч.-изд.л. Тираж 200 экз. Заказ 46.

Нижегородский государственный технический университет.

Типография НГТУ. 603600, Н. Новгород, ул. Минина, 24.

С

Нижегородский государственный

технический университет, 2005

Содержание

Введение………………………………………………………………………
1. Анализ задания к курсовой работе и алгоритм ее выполнения…………..
2. Принципы выбора оптимальных решений в условиях полной неопределенности ……………………………………………………………...
2.1. Сущность проблемы неопределенности в экономических задачах. Факторы неопределенности. Классификация задач принятия оптимальных решений в условиях неопределенности………………………
2.2. Методология выбора оптимального решения в условиях неопределенности………………………………………………………………
3. Многокритериальный выбор оптимального решения…………………….
3.1. Сущность проблемы многокритериального выбора. Причины конфликта критериев в экономических задачах……………………………..
3.2. Использование принципа доминирования для многокритериального выбора оптимального решения………………………………………………..
3.3. Использование принципа Парето для многокритериального выбора оптимального решения………………………………………………………
4. Методы формирования окончательного решения…………………….
4.1. Метод формирования комплексных показателей……………………..
4.2. Ранжирование альтернатив……………………………………………...
4.3. Метод выделения главного показателя при переводе остальных в разряд ограничений…………………………………………………………….
5. Использование методов многокритериального выбора в условиях неопределённости ……………………………………………………………..
6. Учёт несовпадающих интересов в условиях многокритериальности …
7. Оформление курсовой работы……………………………………………
8. Пример расчетов……………………………………………………………..
9. Варианты к курсовой работе……………………………………………….
Рекомендуемая литература…………………………………………………….

Введение

Дисциплина «Принятие оптимальных решений в экономике» имеет своей целью освоение студентами принципов и методов выбора оптимальных решений в условиях, максимально приближенных к современным экономическим условиям.

Смысл курсовой работы состоит в сравнительной оценке экономической эффективности капитальных вложений в несколько отраслей промышленности по группе критериев, определяемых в условиях неопределенности и отборе наиболее перспективного варианта. Данная задача достаточно широко распространена в повседневной экономико-управленческой деятельности. В то же время ее решение позволяет студентам эффективно изучить достаточно большое количество принципов и методов принятия оптимальных организационно-экономических решений, поскольку в данной задаче в полной мере проявляются основные проблемы, затрудняющие оптимальный выбор – проблема неопределенности, проблема конфликта критериев и проблема несовпадения интересов.

Курсовая работа выполняется студентами V курса социально-экономического факультета НГТУ в течение 9-го семестра. Тематика курсовых работ соответствует учебным планам и рабочей программе по курсу.

1. Анализ задания к курсовой работе и алгоритм ее выполнения

Исходные данные к курсовой работе по дисциплине «Принятие оптимальных решений в экономике» представляют данные об экономическом состоянии отраслей за по четырем отраслям промышленности, из которых предлагается осуществить выбор наилучшего для инвестирования варианта, с учетом зависимости этих показателей от валового внутреннего продукта России (далее – ВВП). Предложенные показатели экономического положения отраслей (таких показателей в задании два, будем для краткости обозначать их К ₁ и К ₂ соответственно) находятся в определенной корреляционной взаимосвязи с величиной ВВП. Прогнозные значения ВВП (в процентах к уровню 1991 года) с учетом разброса значений задаются исходными данными.

Необходимо сформировать область эффективных решений по двум критериям:

а) с позиций инвестора, выбирающего отрасль для создания нового бизнеса;

б) с позиций местной администрации, решающей вопрос о бюджетной поддержке предпринимательства в этих отраслях,

после чего выбрать компромиссные варианты и из них определить окончательное оптимальное решение.

Для выбора оптимального решения рекомендуется воспользоваться методами выбора оптимальных решений по совокупности критериев в условиях неопределенности, в частности, использовать следующие принципы оптимальности: оптимизма, пессимизма, гарантированного результата, максимума средней эффективности, Сэвиджа, гарантированных потерь.

Таким образом, алгоритм выполнения курсовой работы следующий.

Шаг 1. Применяется принцип оптимизма с точки зрения инвестора по первому критерию экономической эффективности. В качестве неуправляемого фактора (факторы { У_i }) принимается ВВП России, в качестве управляемого (факторы { Х_i }) – название отрасли.

Шаг 2. Данная процедура повторяется для второго критерия экономической эффективности отраслей.

Шаг 3. Требуется применить к множеству рассматриваемых отраслей для оптимистических значений критериев принципы многокритериальной оптимизации принимаемых решений (доминирования и Парето). Ограничивается область эффективных решений по принципу оптимизма и исключаются из рассмотрения неэффективные альтернативы.

Шаг 4. Процедура, описывающая шаги 1 – 3, повторяется для остальных пяти принципов оптимальности в условиях неопределённости. Для каждого из этих принципов формируется своя область эффективных решений.

Шаг 5. Области эффективных решений, построенные с опорой на все шесть принципов, объединяются по правилам объединения множеств – если та или иная отрасль вошла в область эффективных решений по одному из принципов, то она включается и в общую область эффективных решений.

Шаг 6. Процедура, описывающая шаги 1 - 5, повторяется для местной администрации (требования к критериям при этом меняются в соответствии с интересами бюджета). Формируется область эффективных решений для местной администрации.

Шаг 7. Область компромиссных вариантов определяется как совокупность отраслей, включаемых в область эффективных решений как инвестором, так и местной администрацией (по правилу пересечения множеств). Принцип пессимизма при формировании множества компромиссных решений не учитывается, так как этот принцип не предусматривает определение наиболее эффективного варианта и нужен только для оценки нижней границы эффективности.

Шаг 8. Осуществляется выбор окончательного решения. Для окончательного выбора можно использовать следующие методы:

- формирование комплексных показателей;

- метод ранжирования;

- выделение главного показателя при ограничении на второй.

Главными при выборе окончательного решения признаются интересы инвестора. Интересы бюджета могут (и должны) учитываться при формировании системы ограничений.

Шаг 8. Выводы по проделанной работе.

2. Принципы выбора оптимальных решений в условиях полной неопределенности

2.1. Сущность проблемы неопределенности в экономических задачах. Факторы неопределенности. Классификация задач принятия оптимальных решений в условиях неопределенности

В хозяйственно-экономической деятельности часто приходится сталкиваться с ситуациями, когда те или иные факторы, оказывающие ощутимое (иногда – даже определяющее) воздействие на результаты реализации управленческих решений, изменяются непредсказуемым образом. Действие этих неуправляемых факторов вносит существенные поправки в последствия тех или иных хозяйственных мероприятий, так что результаты производственно-хозяйственной деятельности могут в итоге совершенно не соответствовать предполагаемым или запланированным. В литературе [1], [4] указываются следующие источники неопределенности:

* необходимость принятия управленческих решений на основе недостаточной и/или недостоверной информации;

* наличие в рыночной среде факторов, не контролируемых со стороны хозяйствующего субъекта (рыночные цены, спрос, курсы ценных бумаг и др.) и нестабильность этих факторов;

* влияние на эффективность управленческих решений природных факторов, всегда труднопредсказуемых;

* системные явления в экономических системах - наличие несогласованности целей между различными подсистемами хозяйствующего субъекта;

* действия конкурентов, поставщиков, покупателей и других агентов маркетинговой среды предприятия, чьи интересы не совпадают с интересами самого предприятия, а в ряде случаев – даже противоположны им;

* наличие управляющих подсистем, регулирующих деятельность хозяйствующих субъектов (государственных, региональных и муниципальных органов власти), чьи действия носят целенаправленный характер, поэтому также труднопредсказуемы;

* нестабильность законодательной базы, в рамках которой осуществляются экономические процессы;

* так называемый производственно-технологический риск, связанный с возможностью поставки некачественной продукции, аварий и катастроф.

По виду факторов неопределенности задачи принятия решений делятся на следующие классы [1], [4]:

а) принятие решений при действии неуправляемых факторов, которые не являются результатом чьих-либо целенаправленных действий, а служат элементами объективного внешнего окружения, в рамках которого осуществляется деятельность хозяйствующего субъекта;

б) принятие решений в условиях конфликта интересов (неопределенность обусловлена наличием как минимум двух сторон в экономическом процессе, каждая из которых имеет свои интересы, причем эти интересы абсолютно противоположны – достижение одной из сторон положительного результата приводит к отрицательному результату остальных участников);

в) принятие решений в условиях несовпадающих интересов (отличается от предыдущего тем, что принципиально возможным становится достижение положительного результата одновременно всеми участниками экономического процесса, целевые установки разных сторон в некоторых аспектах могут совпадать).

Таким образом, задача выбора оптимального решения в условиях полной неопределенности разбивается на три подзадачи:

1) определение вида неопределенности;

2) построение адекватной экономико-математической модели неопределенности;

3) сравнение альтернатив и выбор наилучшего варианта в условиях неопределенности.

Поставленная задача относится к классу задач выбора оптимального решения в условиях действия неконтролируемых факторов, поэтому для ее решения может быть использован аппарат т.н. «игр с природой».

2.2. Методология выбора оптимального решения в условиях неопределенности

После вычисления значений показателей эффективности К ₁ и К ₂, соответствующих всем значениям ВВП от 76,1% до 79%, можно заполнить матрицу игры. Матрица выбора имеет вид, аналогичный табл.3.

Значения К_ij в данной таблице – значение показателя соответственно К ₁ или К ₂ для i -й отрасли и j -го значения ВВП из интервала [76,1%; 79%].

Таким образом, имеется целый набор возможных значений критерия К ₁ (или К ₂), причем какое именно значение из этого набора примет в действительности критерий, невозможно сказать даже с той или иной степенью вероятности. Тем не менее, необходимо принять оптимальное решение исходя из имеющихся данных.

Таблица 1

Матрица выбора оптимального решения в условиях полной неопределенности для одного из критериев эффективности

У Х	76,1	76,9	77,6	78,3
Отрасль 1	К 1,1	К 1,2	К 1,3	К 1,4	К 1,5
Отрасль 2	К 2,1	К 2,2	К 2,3	К 2,4	К 2,5
Отрасль 3	К 3,1	К 3,2	К 3,3	К 3,4	К 3,5
Отрасль 4	К 4,1	К 4,2	К 4,3	К 4,4	К 4,5

Для выбора оптимального решения в условиях неопределенности предлагается шесть принципов [1]:

- принцип оптимизма;

- принцип пессимизма;

- принцип гарантированного результата;

- принцип максимума средней эффективности;

- принцип Сэвиджа;

- принцип гарантированных потерь.

Принцип оптимизма ориентирован на оптимистическое восприятие неопределенности: предполагается, что значения неконтролируемых факторов сложатся для хозяйственного объекта, реализующего управленческое решение, наиболее благоприятным образом. Формулировка данного принципа такова:

Оптимальным решением является вариант, обеспечивающий наилучшее значение критерия отбора при наилучшем возможном значении фактора неопределенности.

Если эффективность вариантов возрастает с увеличением показателя К ₁ (К ₂), т.е. данный показатель отражает некий положительный эффект (К_ij = Э _ij), то для выбора оптимального решения в соответствии с данным принципом необходимо выбрать максимальный элемент в каждой строке табл. 3. Тогда оптимальному выбору будет соответствовать та строка, для которой данное значение максимально. Математически это правило выражается следующей записью:

.

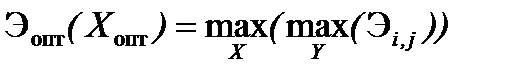Аналогично, если с увеличением К ₁ (К ₂) эффективность i -го варианта снижается, т.е. данный показатель характеризует либо затраты (К_ij = З _ij), либо некоторый отрицательный результат (К_ij = У _ij), то правило выбора оптимального решения по принципу оптимизма следующее:

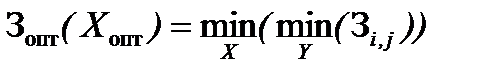
Принцип пессимизма исходит из того, что неблагоприятным образом могут сложиться не только неконтролируемые, но и управляемые факторы. На первый взгляд данное положение кажется абсурдным. Однако в действительности возможны различные непредвиденные обстоятельства, способные помешать использовать контролируемые факторы наилучшим образом. Принцип пессимизма позволяет оценить наихудший из возможных результатов, чтобы решить, стоит ли вообще участвовать в решении данной управленческой задачи. Формулировка принципа пессимизма звучит так:

Оптимальным решением является вариант, обеспечивающий наихудшее значение критерия отбора при наихудшем состоянии факторов неопределенности.

Согласно принципу пессимизма, для показателей положительного эффекта оптимальное решение Х _опт выбирается так, что

.

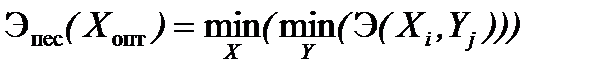Для случая ущерба или затрат правило имеет следующий вид:

.

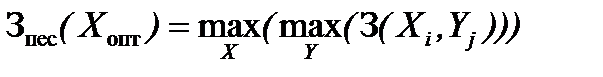Принцип гарантированного результата является наиболее распространенным принципом выбора оптимального решения в условиях неопределенности. Исходной посылкой данного принципа служит стремление субъекта, осуществляющего выбор оптимального решения, свести к минимуму риск при реализации принимаемого решения. За счет использования принципа гарантированного результата удается свести этот риск к 0. При принятии решения по принципу гарантированного результата исходят из того, что значения неконтролируемых факторов могут быть любыми, но управляемые факторы должны при этом быть использованы наилучшим образом – так, чтобы даже при наихудшем стечении обстоятельств получить приемлемый положительный результат. Формулировка принципа:

Оптимальным решением является вариант, обеспечивающий наилучшее значение критерия отбора при наименее благоприятном состоянии факторов неопределенности.

Порядок действий при выборе оптимального решения Х _опт по принципу гарантированного результата для показателей полезного эффекта следующий: в каждой строке матрицы (табл. 3) выбирается минимальный элемент. Затем в качестве оптимального решения выбирается значение управляемых факторов, соответствующее той строке, где это минимальное значение будет наибольшим. Математически это правило описывается условием

,

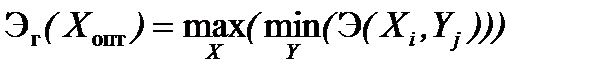а для критериев затрат или ущерба – условием:

.

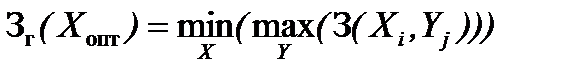При выборе оптимального решения по принципу максимума средней эффективности исходят из некоторого компромиссного варианта между принципом оптимизма и принципом гарантированного результата. Тот, кто руководствуется при выборе оптимального решения данным принципом, не рассчитывает на наилучшее стечение обстоятельств, но и не хочет подстраховываться на самый худший случай. Правило выбора решения в данном случае следующее. Для каждого значения контролируемых факторов определяется среднее значение критерия отбора:

,

.

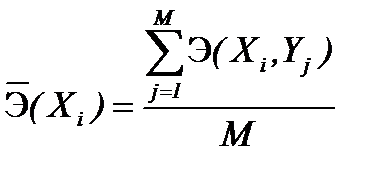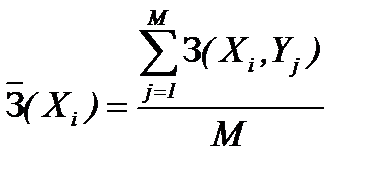Выбор оптимального решения на основе критерия максимума средней эффективности для показателей полезного эффекта осуществляется на основании правила

,

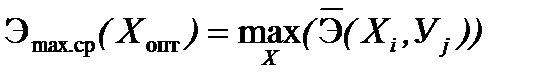а для показателей затрат и отрицательных результатов:

.

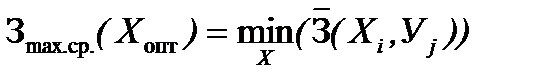Обобщая, можно сформулировать принцип максимума средней эффективности следующим образом:

Оптимальным решением является вариант, обеспечивающий наилучшим значение критерия отбора, усредненное по всем возможным значениям фактора неопределенности.

В ряде случаев важен не столько сам полезный результат, сколько его надежность. В этом случае правилом выбора оптимального решения в условиях неопределенности служит принцип минимума дисперсии:

Оптимальным решением является вариант, обеспечивающий минимальное значение дисперсии критерия отбора.

Для определения дисперсии используется формула несмещенной оценки

.

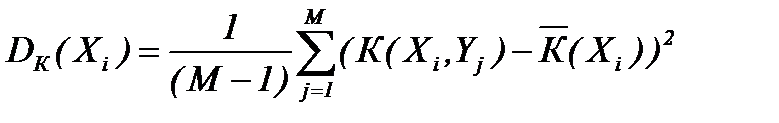Поскольку в данном случае правило выбора оптимального решения для показателей полезного эффекта и затрат одно и то же, то формулу дисперсии можно не конкретизировать. Правило выбора оптимального решения в этом случае имеет вид:

.

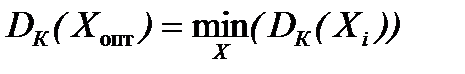Чтобы совместить выбор оптимального решения по максимуму эффективности и максимуму надежности применяют метод определения коэффициента вариации. Коэффициент вариации определяется следующим образом:

.

Для показателей полезного эффекта правило выбора оптимального решения выглядит следующим образом:

.

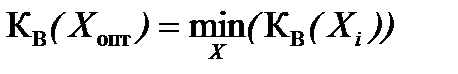Принцип гарантированного результата, находящий наиболее широкое применение при выборе оптимальных решений, имеет существенный недостаток: он ориентирован на наихудшие значения неконтролируемых факторов. Между тем, если неконтролируемые факторы сложатся более благоприятным образом, то выбранная стратегия может оказаться неоптимальной и предприятие понесет значительный проигрыш. Для учета этого обстоятельства был предложен принцип Сэвиджа (принцип минимизации сожаления). Свое название он получил от того, что для выбора оптимального решения в соответствии с данным принципом необходима т.н. матрица сожалений. Элемент ее С _ij представляет собой проигрыш лица, принимающего решение, от неоптимальности выбранной стратегии при данном значении фактора неопределённости и определяется следующим образом. Для показателя полезного эффекта формула расчета сожаления, соответствующего значению Э (Х_i, Y_j), такова:

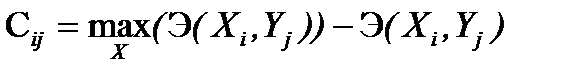. (1)

Аналогично для показателей затрат и отрицательного результата:

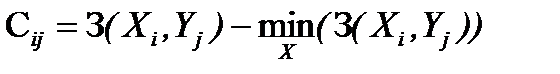. (2)

На основании исходной таблицы (табл.2) и формул (1) и (2)составляется матрица сожалений (табл.4.)

Таблица 4

Матрица сожалений. Иллюстрация к принципу Сэвиджа

У Х	76,1	76,9	77,6	78,3
Отрасль 1	С1,1	С1,2	С1,3	С1,4	С1,5
Отрасль 2	С2,1	С2,2	С2,3	С2,4	С2,5
Отрасль 3	С3,1	С3,2	С3,3	С3,4	С3,5
Отрасль 4	С4,1	С4,2	С4,3	С4,4	С4,5

Таким образом, принцип Сэвиджа может быть сформулирован так:

Оптимальным решением является вариант, обеспечивающий минимальное гарантированное сожаление.

Под сожалением здесь понимается проигрыш вследствие неоптимальности выбранного варианта для текущего значения фактора неопределённости. Иначе говоря, оптимальное решение Х _опт определяется в соответствии с правилом

.

Еще одним принципом выбора оптимального решения в условиях полной неопределенности является принцип гарантированных потерь. В отличие от принципа Сэвиджа, ориентированного на поиск проигрыша от неоптимального выбора собственной стратегии предприятия при заданном значении неуправляемых факторов, этот принцип исходит из того, что предприятие использует свои управляемые факторы наилучшим образом, и стремится минимизировать ущерб, порождаемый неблагоприятным влиянием факторов неопределенности. В основе данного принципа лежит определение потерь, которые возникают в реальном случае по сравнению с идеальным значением неуправляемых факторов. Таким образом, указанный принцип выбора оптимального решения призван частично скомпенсировать недостаток принципа оптимизма – завышенные ожидания от реализации принятого решения. В данном случае субъект, принимающий решения, стремится минимизировать свой проигрыш по сравнению с оптимальным (оптимистическим) вариантом, то есть добиться, чтобы гарантированный результат не слишком сильно отличался от оптимистического.

При выборе оптимального решения по принципу гарантированных потерь формируется т.н. матрица потерь (табл.5).

Таблица 5

Матрица потерь. Иллюстрация к принципу гарантированных потерь

У Х	76,1	76,9	77,6	78,3
Отрасль 1	П1,1	П1,2	П1,3	П1,4	П1,5
Отрасль 2	П2,1	П2,2	П2,3	П2,4	П2,5
Отрасль 3	П3,1	П3,2	П3,3	П3,4	П3,5
Отрасль 4	П4,1	П4,2	П4,3	П4,4	П4,5

Элемент матрицы потерь П _ij для показателей полезного эффекта вычисляется по формуле

,

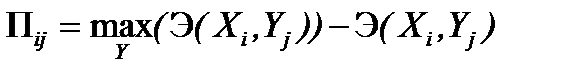а для показателей затрат или отрицательных результатов – по формуле

.

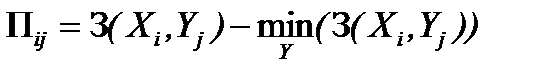Правило выбора оптимального решения – принцип гарантированного результата применительно к матрице потерь:

.

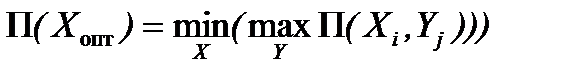Словесная формулировка принципа выглядит следующим образом:

Оптимальным решением является вариант, обеспечивающий минимальные гарантированные потери, порождаемые действием неуправляемых факторов.

Таким образом, существуют 8 альтернативных принципов выбора оптимального решения в условиях полной неопределенности, дающих в общем случае различные результаты. Каким из принципов пользоваться – зависит от специфики задачи и целей субъекта, принимающего решение. Однако многовариантность способов выбора усложняет задачу – появляется дополнительная неопределенность окончательного варианта.

Для практических задач бывает полезно применить все вышеперечисленные принципы. На основании такого анализа появляется возможность исключить из рассмотрения заведомо проигрышные варианты и проранжировать сравниваемые альтернативы.

3. Многокритериальный выбор оптимального решения

3.1. Сущность проблемы многокритериального выбора. Причины конфликта критериев в экономических задачах

Источником проблемы конфликта критериев является необходимость оптимизации сравниваемых вариантов по нескольким взаимосвязанным критериям одновременно. При этом критерии оптимальности изменяются от альтернативы к альтернативе в общем случае несогласованно, поэтому варианты, оптимальные по каждому из критериев в отдельности, не совпадают друг с другом. Как показал итальянский ученый В.Парето, выбор единственного оптимального решения в таких условиях просто невозможен, возможно лишь исключить из множества рассматриваемых альтернатив те, которые заведомо не могут являться оптимальным решением.

Необходимость многокритериальной сравнительной оценки анализируемых вариантов порождается следующими факторами [2]:

а) многомерностью результата принятого решения (любое управленческое решение вследствие всеобщей взаимосвязанности социально-экономических процессов порождает целый комплекс последствий, зачастую измеряемых в совершенно разных величинах – финансово-экономических, социальных, научно-технических, экологических);

б) сложной структурой затрат (в простейшем случае затраты подразделяются на капитальные, вложенные в основные производственные фонды и интеллектуальную собственность, и текущие, отнесенные непосредственно на производство конкретной продукции; в ряде случаев важную роль могут играть также некоторые другие ресурсы, не имеющие прямого денежного выражения - время, человеческие ресурсы и др.);

в) множественностью и противоречивым характером целей, преследуемых при выборе оптимального решения (например, цель одновременного снижения затрат и повышения их отдачи);

Дата добавления: 2015-06-04