Оптимальное передаточное число редуктора в электроприводе

Задача приведения к одному движению при меняющемся передаточном числе редуктора

Ряд электроприводов содержат нелинейные кинематические связи с меняющимся коэффициентом передач между двигателем и рабочим механизмом. Примером передаточного устройства с меняющимся коэффициентом передачи являются кривошипно-шатунный, кулисный и другие подобные механизмы. На рис. показана кинематическая схема электропривода с передаточным устройством в виде кривошипно-шатунного механизма (i≠const). Радиус приведения в них является переменной величиной, зависящей от положения механизма: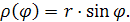

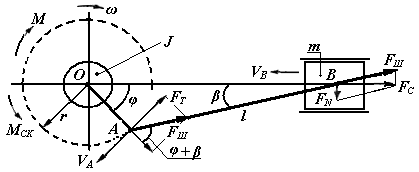
Рис. 2.8 Механическая система с нелинейными кинематическими связями

Представим рассматриваемую систему в виде двухмассовой, первая масса вращается со скоростью ω и имеет момент инерции J, а вторая движется с линейной скоростью V и представляет суммарную массу m элементов, жёстко и линейно связанных с рабочим органом механизма.

Рассмотрим вначале приведение статических усилий и моментов, сделав допущение о пренебрежимо малой величине потерь в кривошипном механизме, т.е. считая его к.п.д. η=1. В этом случае уравнение баланса мощности в кривошипном механизме запишется следующим образом:

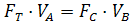, (2.29)

где F_T – тангенциальное усилие, действующее на конце кривошипа с радиусом r и полученное путем разложения и переноса исходного усилия сопротивления движению F_С (рис. 2.8).

Тогда момент сопротивления на валу кривошипа без учета сопротивления трения будет: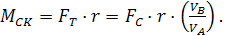

Из разложения сил на рис.2.8 следует, что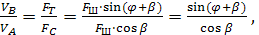

тогда 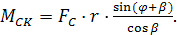(2.30)

Момент сопротивления, приведенный к валу двигателя при наличии редуктора в электроприводе с передаточным числом i:

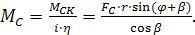(2.31)

При большой длине шатуна l, когда l/r ≥ 5 можно принять, что β≈0, 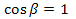и упростить выражение (2.30):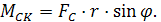

Таким образом, величина М_СК меняется в функции углового пути кривошипного вала φ и имеет небольшую постоянную составляющую, определяемую потерями на трение в кривошипном механизме.

Для приведения моментов инерции и движущихся масс к вращающемуся валу (точка «О») кривошипа составим уравнение баланса кинетической энергии кривошипного механизма в реальной и эквивалентной системах:

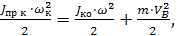(2.32)

где J_пр.к – момент инерции кривошипного механизма, приведенный к валу кривошипа; J_К.0 – момент инерции собственно кривошипа, т.е. деталей, вращающихся вокруг центра кривошипа; m – масса ползуна; V_B – скорость движения ползуна.

В данном выражении ввиду малости массы момента инерции шатуна составляющая запаса кинетической энергии шатуна при его вращательном и поступательном движениях не учитывается. С учетом известной зависимости V=ω·r приведенный момент инерции кривошипного механизма будет

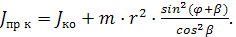(2.33)

Это соотношение упрощается для кривошипных механизмов при β≈0:

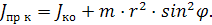(2.34)

С учетом наличия в электроприводе редуктора момент инерции электропривода, приведенный к валу двигателя, имеющего собственный момент инерции J_Д, будет равен:

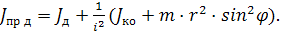(2.35)

Примерный график изменения приведенного момента инерции J_ПР.Д=f(φ) показан на рис.2.9.

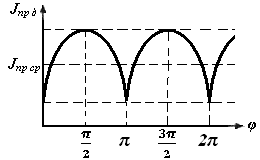
Рис.2.9 Зависимость приведенного момента от угла поворота шатуна

При проектировании электропривода необходимо обеспечить требования технологического процесса и, в частности, необходимую скорость рабочей машины. Таким технологическим требованием может быть и максимальное быстродействие привода в неустановившихся режимах. Обеспечить это требование можно, в частности, изменением передаточного числа редуктора между двигателем и рабочей машиной при выборе двигателя с различной номинальной скоростью без учета системы управления.

Для электроприводов, работающих в длительном режиме работы, при выборе электродвигателя передаточное число редуктора является определяющим значение одного из критериев оптимальности – минимума стоимости оборудования. Действительно, чем выше передаточное число редуктора, т. е. чем он оказывается более сложным по конструкции, например, с червячным зацеплением, большим числом кинематических пар, тем стоимость редуктора оказывается выше. Используя редуктор с меньшим передаточным числом (при неизменной технологической скорости рабочей машины) требуется применение электродвигателя с большей стоимостью из-за технологических особенностей конструкции и стоимости их компонент.

Таким образом, уменьшение передаточного числа ведет к увеличению стоимости двигателя и уменьшению стоимости редуктора. Оптимальное передаточное число i_опт находится на пересечении кривых стоимости редукторов и двигателей, как показано на рис.2.10. При реальном проектировании электропривода необходимо построить кривые С=f(i) для двигателей выбранного типа и ряда серийных редукторов. Двигатель и редуктор выбираются по передаточному числу в окрестностях точки пересечения кривых С=f(i) путем выполнения сравнительных технико-экономических расчетов.

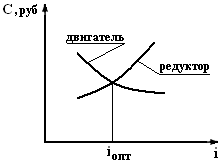
Рис. 2.10 К выбору оптимального передаточного числа редуктора ЭП

При повторно-кратковременном режиме работы электропривода выбор скорости двигателя и передаточного числа редуктора оказывается более сложным. Экономическая эффективность электропривода в режиме определяется не столько капитальными затратами, сколько производительностью рабочей машины, прямо зависящей от быстродействия пусковых и тормозных режимов работы двигателя.

Продолжительности пуска и торможения электропривода существенно зависят от величины передаточного числа редуктора.

Время движения при пуске и торможении механизма t_м определяются через приведенные к валу механизма переменные как:

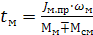, (2.36)

где J_м.пр – момент инерции всех вращающихся частей (двигатель, рабочая машина), приведенный к валу механизма;

М_м – пусковой или тормозной момент двигателя, приведенный к валу механизма;

М_см – момент статического сопротивления на валу механизма (знак (+) в (2.36) - для режима торможения, а знак (-) – для режима пуска рабочей машины.

С учетомпотери в передачах через к.п.д. (η) получим значения времени пуска и торможения электропривода:

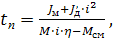(2.37)

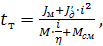(2.38)

где J_М – момент инерции механизма;

J'_Д – момент инерции двигателя и элементов на его валу (муфта, датчики, быстроходный вал редуктора);

М – пусковой или тормозной момент двигателя (при ступенчатом пуске – среднее значение момента).

Из полученных уравнений видно, что t_П=f(i) и t_Т=f(i) - экстремальные функции, имеющие минимальное значение при i=i_опт. Оптимальные значения i_опт.п при пуске или i_опт.т при торможении определяются исследованием уравнений (2.37) и (2.38) на экстремум из условия:

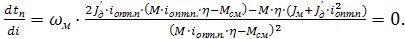
Приравняв нулю числитель, получим 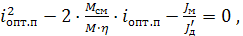решениякоторого для режимов пуска и торможения будут:

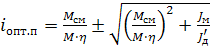(2.39)

Перед корнем надо учитывать при расчетах лишь знак (+). При знаке (-) i_рпт.п не имеет физического смысла (i_опт.п<0).

Аналогично можно получить выражение для расчета оптимального передаточного числа при торможении:

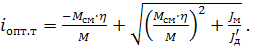(2.40)

Так как i_опт.п ≠ i_опт.т, то при реальных расчетах принимают среднее, либо средневзвешенное значение по известным выражениям.

Если привод имеет большие моменты инерции и незначительную статическую нагрузку, т.е. при 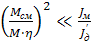, величина оптимального передаточного числа приближенно может быть найдена по упрощенной формуле:

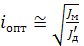. (2.41)

Расчетное значение i_опт, как правило, не совпадает с конкретными передаточными числами серийных редукторов. В этом случае при выборе передаточного числа лучше принимать ближайшее большее значение, так как при этом потери ускорения механизма будут меньше.

Дата добавления: 2015-06-04