Средняя арифметическая величина и ее свойства

Самая простая статистическая ха­рактеристика всякого вариационного ряда — средняя арифметическая величи­на [3-5], представляющая собой абст­рактную математическую величину. Средняя арифметическая величина ха­рактеризует всю совокупность в целом, а не отдельные части совокупности.

В современной литературе по био­метрии выборочную среднюю арифме­тическую величину принято обозначать символом х, тогда как среднюю ариф­метическую величину любой генераль­ной совокупности или выборочную среднюю, представляющую генераль­ную совокупность (при п —> °°), обозна­чают символом М.

Чтобы вычислить среднюю ариф­метическую величину, в простейшем случае достаточно сложить все имеющи­еся значения признака и сумму этих зна­чений разделить на число случаев. В общем виде формула для вычисления средней арифметической величины бу­дет иметь вид

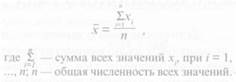
Для любого вариационного ряда общая формула для вычисления средней арифметической величины такова:

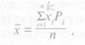
где числитель есть сумма произведении всех значений признака х1 от i = 1,...., к (к — чис­ло классов), умноженных на свои частоты Рх., а знаменатель — общее число всех слу­чаев п.

Если надо найти общую среднюю арифметическую величину для несколь­ких выборок, имеющих разную числен­ность, следует среднюю арифметичес­кую величину каждой выборки умно­жить на свою численность (или, как го­ворят, «взять со своим весом»), все эти произведения сложить и разделить на общую численность всех групп (на об­щую сумму «весов»). Такая средняя арифметическая величина носит назва­ние взвешен пой средней арифме­тической величины. Формула для ее вычисления имеет вид

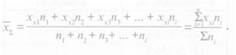
Пример. Вычислить взвешенную сред­нюю арифметическую величину при следу­ющих данных по измерению длины тела для трех выборок:

Прямым способом определения средней арифметической величины, ког­да вариационный ряд состоит из боль­шого числа значений, в большинстве случаев не пользуются, так как это слишком кропотливо и неудобно. По­этому на практике часто пользуются другими, более удобными сокращенны­ми приемами. Они основаны на опреде­ленных математических свойствах сред­ней арифметической величины [1; 3; 4].

Первое свойство — сумма всех от­клонений от средней арифметической величины равна нулю, т. е.

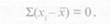
Например, имеем пять чисел: 10,11. 12. 13. 14. Как указывалось выше, х для этого ряда равен 12.

Отклонения от средней величины бу­дут следующие: 10 - 12 = -2; 11 - 12 = -1; 12-12 = 0; 13-12 = +1; 14-12 = +2.

Сумма отклонений -2-1+0+1+2 = 0.

Это свойство отклонений средней арифметической величины использует­ся для проверки правильности ее расче­та: если ∑ (х₁ — x^-) оказалась не равной нулю, значит допущена ошибка в вы­числениях.

Второе свойство — сумма квадра­тов отклонений от средней арифмети­ческой величины всегда меньше суммы квадратов отклонений от любого дру­гого значения вариационного ряда, т. е.

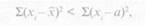
где а — любое значение признака, не рав­ное х.

Например, имеем пять чисел: 10.11, 12, 13, 14. Как указывалось выше, х для этого ряда равен 12.

Квадраты отклонений от средней арифметической будут следующие: (-2)² = 4; (-1)² = 1; (О)²' = 0; (+1)² - 1; (+2)² = 4.

Сумма квадратов отклонений 4+1+0 + 1 + 4 = 10.

Квадраты отклонений от числа 10: (0)² = 0; (I)² = 1; (2)^; = 4; (if = 9; (4)² = 16.

Сумма квадратов отклонений 0+1+4 + 9 + 1 = 30, т. е.

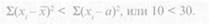
Третье свойство — если каждое из значений вариационного ряда увели­чить или уменьшить на одну и ту же ве­личину, то и средняя арифметическая величина увеличится или уменьшится на ту же величину, т. е.

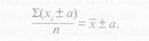
Например, если ко всем указанным выше числам (10, 11, 12, 13 и 14) прибавить пять единиц, то и средняя арифметическая величина увеличится на пять единиц (х = 17). Если соответственно из каждого числа вы­честь три единицы, то и средняя арифмети­ческая величина уменьшится на три едини­цы (х = 9).

Четвертое свойство — если каж­дое из значений вариационного ряда умножить или разделить на одно и то же число, то средняя арифметическая вели­чина увеличится или уменьшится во столько же раз, т. е.

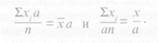
Если в нашем примере все числа увеличить в 10 раз, то средняя арифме­тическая величина увеличится в 10 раз (х = 120), и если каждое из этих чисел разделить на 10, средняя арифметичес­кая уменьшится в 10 раз (х = 1,2).

Три последних свойства значитель­но упрощают и облегчают работу при вычислении средней арифметической величины и других статистических па­раметров вариационных рядов, имею­щих большую численность.

Дата добавления: 2015-06-04