Вычисление основных статистических параметров для вариационного ряда длин тела (х) способом моментов (девочки 14 лет, г. Москва, 1999 г.)

Вычисление средней арифметичес­кой величины х. Для получения этой ве­личины численность в каждом классо­вом интервале умножают на условное отклонение в этом же классе, т. е. числа Р_х (графа 3) умножают на числа а_x (гра­фа 4), учитывая знак натурального чис­ла. Полученные результаты Р_xа_x запи­сывают в графу 5, суммируют результа­ты, учитывая знак, и получают ∑ Р_xa_x. Делят сумму произведений ∑ Р_xa_x на чис­ло случаев и получают момент первой степени v_lx.

Момент первой степени показыва­ет, на какую долю интервала условная средняя величина больше или меньше средней арифметической величины. В том случае, если момент первой степе­ни равен 0, средняя арифметическая ве­личина и условная средняя величина совпадают (исходя из первого свойства средней арифметической величины).

Среднюю арифметическую величи­ну х вычисляют по формуле

где А — условная средняя величина; i_x — классовый интервал в единицах измерения; v. — момент первой степени.

Вычисление среднего квадратично­го отклонения s. Для нахождения этой величины умножают численность значе­ний в каждом классовом интервале на квадрат условных отклонений в тех же классах или, что то же самое, числа а_x

(графа 4) умножают на произведение ∑Р_xa_x (графа 5) построчно. В обоих слу­чаях будет получен один и тот же резуль­тат ∑Р_xa_x ². Просуммировав эти произве­дения, получают ∑Р_xa_x ², а поделив эту сумму на число случаев п — момент второй степени.

Момент второй степени есть сум­ма квадратов отклонений от условной средней величины, выраженная в услов­ных единицах.

Если условная средняя равна сред­ней арифметической величине, то фор­мула для расчета среднего квадратично­го отклонения имеет вид:

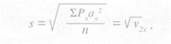
т. е. среднее квадратичное отклонение в этом случае равно корню квадратному из момента второй степени.

В случае если условная средняя от­клоняется от средней арифметической на величину момента первой степени

то для вычисления среднего квадратичного отклонения из суммы квадратов отклонений от условной средней величины (т. е. момента второй степени v_2x) следует вычесть квадрат отклонения условной средней от средней ' арифметической величины (т. е. момент первой степени в квадрате V_lx²). Затем из этой разности извлекается квадратный корень и умножается на классовый ин­тервал.

Таким образом, формула для вы­числения среднего квадратичного от­клонения принимает вид:

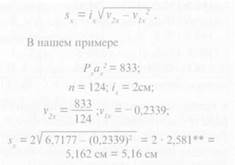
Таким образом, средняя арифмети­ческая величина длин тела у девочек для данной выборки х = 157,98 см, среднее квадратичное отклонение л- = 5,16 см.

После того как рассчитаны основ­ные параметры вариационного ряда, приступают, если это требуется, к пост­роению вариационной кривой. Как ука­зывалось выше (гл. 3, п. 2), величина классового интервала в этом случае дол­жна увеличиваться.

Существует определенное правило для нахождения границ классовых интервалов. Кривая будет построена пра­вильно в том случае, если значение ме­дианы будет близким к среднему клас­совому интервалу. В зависимости от это­го определяют границы классового ин­тервала, в котором находится медиана. Границы классов вверх и вниз от этого класса вычисляют путем последователь­ного прибавления (или вычитания) классового интервала к нижним и верх­ним границам классов.

Для рассматриваемого примера уже было вычислено значение медианы, равное 158,19 см. Значит, за середину классового ин­тервала следует принять 158,45 см (=158,5 см). Исходя их найденного классового ин­тервала / = 4 см (гл. 3, п. 2), нижней грани­цей центрального класса будет значение 155,5 см, верхней—159,4 см.

Границами классовых интервалов вверх от центрального класса будут значе­ния 151,5-155, 4 см и так далее, вниз 159,5-163,4 см и так далее (см. табл. 3.4).

Дата добавления: 2015-06-04