Достоверность различий выборочных распределений частот антропометрических признаков. Асимметрия и эксцесс

Ни одно эмпирическое распределе­ние антропометрических признаков, как правило, не имеет точного совпадения с теоретической кривой нормального распределения.

Расхождения между эмпирическим и теоретическим распределениями чис­ленно оцениваются с помощью особых критериев. При этом исследуемое рас­пределение рассмаривается как резуль­тат выборки, имеющей нормальный за­кон распределения, и в силу ограничен­ности ее объема не вполне совпадающее с ним. Найдя численное значение рас­хождения с помощью какого-либо кри­терия, определяют вероятность того, что случайная выборка дает расхождение, достигающее такого же или большего значения. Различия могут считаться слу­чайными, если эмпирическое значение выбранного критерия не превышает за­данного порога вероятности. Таким способом определяют соответствует ли наблюдаемое распределение закону нор­мального распределения исходной сово­купности, из которой взята выборка.

Наиболее распространенным кри­терием соответствия является кри­терий «хи-квадрат» — χ² Функция χ² представляет собой сумму квадратов отклонений эмпирических численностей от теоретической, поделенных на теоре­тическую численность:

где f — эмпирические f₁— теоретические частоты в каждом i -м классе значений при­знака [6].

Эта функция хорошо изучена, со­ставлены таблицы ее вероятностей Р ( χ ²) (см. приложение 6).

Различие между эмпирическим и теоретическим распределением считает­ся достоверным, если полученный кри­терий χ² больше табличною с вероятно­стью 0.99. Конкретные примеры оцен­ки различий между эмпирическим и тео­ретическим распределением приведены в приложении 6.

Ранее считалось, что распределе­ние всех без исключения антропометрических признаков подчинено закону нормального распределения. Однако работы в области прикладной антропо­логии показали, что далеко не все при­знаки имеют нормальное распределение частот. Оказывается, что этой законо­мерности в достаточной мере подчиня­ются лишь признаки, связанные с раз­мерами скелета. В то же время, все признаки, связанные с жироотложением, т. е. обхватные размеры, дают эмпири­ческие распределения, значительно ук­лоняющиеся от нормального [1; 7; 15].

Для расчета теоретического рас­пределения этих признаков прибегают к особому математическому приему, который позволяет превратить распре­деления, отклоняющиеся от нормально­го, в нормальные. Такое преобразова­ние можно провести при помощи соот­ветствующей преобразующей функции. Сама случайная величина х может не иметь нормального распределения, но ее функция при правильном выборе будет подчиняться закону нормального рас­пределения. Вид преобразующей функ­ции зависит от природы изучаемого яв­ления. Для преобразования распределе­ний обхватпых антропометрических признаков применяется метод лога­рифмической трансформации с использованием функции [1; 8-10; 15]:

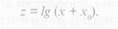
Более подробно этот метод описан в конце параграфа.

Преобразования эмпирических распределений, отклоняющихся от нор­мальных, необходимы, так как если при расчете теоретических распределений пренебречь отклонением и вести разра­ботку данных исходя из нормального распределения признаков возникнет погрешность из-за несоответствия эмпи­рических и теоретических кривых рас­пределения. При разработке размерной типологии эта погрешность приведет к тому, что часть людей не найдет для себя одежды, а для части людей одежда, на­оборот, будет в избытке. Погреш­ность П, % может быть вычислена как полусумма абсолютных разностей (без учета знака) между эмпирическими и теоретическими частотами, деленная на общую численность выборки [5]: тому, что часть людей не найдет для себя одежды, а для части людей одежда, на­оборот, будет в избытке. Погреш­ность П, % может быть вычислена как полусумма абсолютных разностей (без учета знака) между эмпирическими и теоретическими частотами, деленная на общую численность выборки [5]:

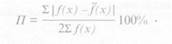
Погрешность, превышающая 5%, считается значимой.

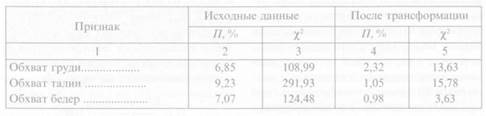
Так для основных обхватных при­знаков в группе женщин (21-59 лет) (по данным 1990 г.) величина погрешности выражается цифрами, приведенными в табл. 3.7.

Согласно приложению 6, табл. 3 доверительные уровни значимости χ² для приведенных признаков соответ­ственно равны:

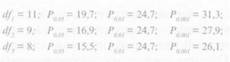
Высокие цифры погрешности П, % и критерия х^{2 в} табл. 3.7, которые в зна­чительной степени превышают приве­денные выше значения доверительных уровней значимости, говорят о том, что исходные распределения обхватных признаков в значительной степени от­личаются от нормальных. В табл. 3.7 приведены значения тех же показателей после обработки данных методом лога­рифмической трансформации. Как ви­дим, распределения после преобразова­ния стали нормальными. Более подроб­но об эффективности применения дан­ного метода при построении размерной типологии будет сказано в главе 4.

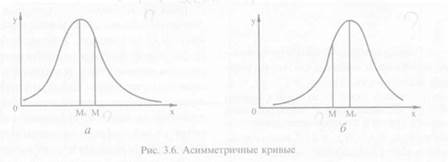
Погрешность, возникающая из-за несоответствия эмпирических и теорети­ческих кривых распределения, является следствием наличия в эмпирическом распределении асимметрии и эксцесса. Как уже отмечалось, теоретическая кри­вая нормального распределения симмет­рична и средняя арифметическая вели­чина совпадает с модой и медианой. В то же время любая эмпирическая кри­вая обнаруживает большую или мень­шую асимметрию и, как правило, сред­няя арифметическая величина, мода и медиана не совпадают друг с другом. Асимметричные кривые показаны на рис. 3.6.

При асимметричном распределе­нии наблюдается увеличение частот в правой или левой половине кривой. Средняя арифметическая величина в таком распределении перемещается в ту сторону кривой, где находится большая численность. Условно принимают асим­метрию положительной при увеличении правой половины кривой и отрицатель­ной, если увеличена левая половина кри­вой. При положительной асимметрии (см. рис. 3.6, а) средняя величина нахо­дится справа от наиболее часто встре­чающегося значения признака — моды, т. е. М > М, при отрицательной — сле­ва от нее (см. рис. 3.6, б), т. е. М < М₀. Следует отметить, что для антропомет­рических признаков характерна преиму­щественно правосторонняя (положи­тельная) асимметрия [4].

Значения погрешности и критерия х² Таблица 3.7

Помимо асимметрии, у некоторых кривых можно подметить еще одну особенность: наличие высоко- или плоско-вершинности, или эксцессивности (экс-цессивные кривые изображены на рис. 3.7). Высоковершинность, или эксцес-сивность, характеризуется значитель­ным увеличением численностей в клас­се, где находится средняя арифметичес­кая величина, и уменьшением в классах с крайними значениями признака. В этом случае кривая распределения 1 имеет вид острой пирамиды с расширен­ным основанием. Вершина кривой, как видно из рисунка, в этом случае лежит выше вершины нормальной кривой 2. Такой эксцесс принято считать положи­тельным. В случае, если вершина кри­вой распределения 3 лежит ниже верши­ны нормальной кривой, эксцесс отрица­тельный [4].

Для каждого вариационного ряда можно рассчитать количественную ха­рактеристику асимметрии и эксцесса: коэффициенты асимметрии γ, и эксцесса γ₂.

Для определения коэффициентов асимметрии и эксцесса, так же как при вычислении средней арифметической величины и среднего квадратичного отклонения, используется метод момен­тов. При определении коэффициента асимметрии пользуются суммой треть­их степеней отклонений от средней арифметической величины х, деленной на общее число случаев, т. е.

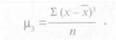
При определении коэффициента эксцесса используется сумма четвертых степеней отклонений от средней ариф­метической величины, деленная на об­щее число случаев, т. е.

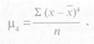
Характеристики µ₃ и µ.₄ носят на­звание центральных моментов соответ­ственно третьей и четвертой степени.

Центральные моменты харак­теризуют отклонения от средней ариф­метической величины.V, деленные на об­щее число случаев п. Таким образом, центральным моментом первой степени будет сумма отклонений первой степени от х, деленная на общее число случа­ев:

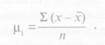
Центральным моментом второй степени будет сумма отклонений второй степени от х, деленная на общее число случаев:

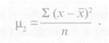
В том случае, если отклонения бе­рут не от средней арифметической вели­чины, а от условной средней А, прини­маемой за 0, то момент называется на­чальным. Так, начальный момент пер­вой степени от условной средней величины выражается как 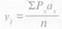а момент второй степени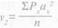

При вычислении коэффициентов асимметрии и эксцесса также удобней пользоваться отклонениями от услов­ной средней величины, а не от средней арифметической величины, так как в этом случае можно использовать услов­ные отклонения. Начальные моменты третьей и четвертой степени будут вы­ражаться как суммы отклонений треть­ей и четвертой степени от условной сред­ней величины в условных единицах, де­ленные на общее число случаев:

Между центральными и начальны­ми моментами имеется соответствую­щая зависимость. Так, µ₄ = v ₂- v ₁² т. е. центральный момент второй степени есть не что иное, как s². Центральный момент третьей степени определяют по формуле µ₃ = v ₃- 3 v ₃ v ₁ + 2v₁³, а централь-ный момент четвертой степени — по формуле µ₄ = v₄- 4v₃v₁ + 6v₂v₁ - 3 v₁⁴.

Вычислив значения центральных моментов второй, третьей, четвертой степени (центральный момент первой степени, как известно, всегда равен нулю), переходят к вычислению коэффи­циентов асимметрии и эксцесса. Так, коэффициент асимметрии γ вычисляют путем отнесения центрального момента третьей степени к среднему квадратич-

ному отклонению в кубе, т. е. γ₁ =µ₃/ s³ Приведение к s³ нужно для того, чтобы можно было оперировать с числом не именованным, а отвлеченным и сравни­вать коэффициенты асимметрии и экс­цесса в различных рядах.

Как показывает анализ, в вариаци­онных рядах, не отклоняющихся от нормального, µ₄=3µ₂² отсюда µ₄/µ₂²= µ₄/s₂²=3

В эксцессивном ряду эта величина бу­дет больше трех. Поэтому формула для расчета коэффициента эксцесса имеет вид:

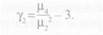
Степень выраженности асимметрии и эксцесса указывает на отклонение дан­ного распределения от нормального. Если кривая симметрична, то γ₁ = 0, γ₂ = 0. Однако из этого еще не следует, что при γ₁ и γ₂, не равных нулю, распределе­ние нельзя считать нормальным; возмож­ны случайные отклонения эмпирического ряда от нормального, которые при достаточно большой величине выборки -могут и не возникнуть. В приложении 7 приведены граничные значения коэффи­циентов асимметрии γ₁ и эксцесса γ₂, за­висящие от величины выборки /; при раз­личных степенях вероятности. Если по­лученные значения коэффициента асим­метрии и эксцесса (при заданном п) мень­ше или равны первому порогу вероятно­сти Р _0.95, то распределение можно считать нормальным. Коэффициенты асиммет­ рии и эксцесса следует считать значимы­ми, а отклонение выборочного распре­деления от нормального — существен­ным, если оно превышает первый и тем более второй порог вероятности Р_0.99(см. приложение 7).

В качестве примера приведем схему рас­чета коэффициентов асимметрии γ₁ и эксцес­са γ₂, для данных, представленных в табл. 3.8.

Для этого примера n = 104; ∑ Р_xа_x=- 59 ∑ Р_xа_x²= 1333; ∑ Р_xа_x³ = -2319; ∑ Р_xа_x⁴= 50965 v_lx=- 0,5673; v_2x= 12,8173; v_3x = - 22,2981 v_4x = 490,0481.

По формулам

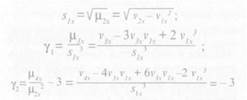
при условии µ_2x² = s_1x⁴ — 156.137 5 рассчи­тывают значения S _1x = (1/2)( l 2,4955) - 3,535; γ₁ = -0,0192 = -0,02: γ₂ = -0,0290 = -0,03.

При помощи коэффициентов асим­метрии и эксцесса можно непосредствен­но определить погрешность П (%), ко­торая, как уже было сказано, получает­ся из-за несоответствия друг другу эм­пирических и теоретических кривых распределения [II]:

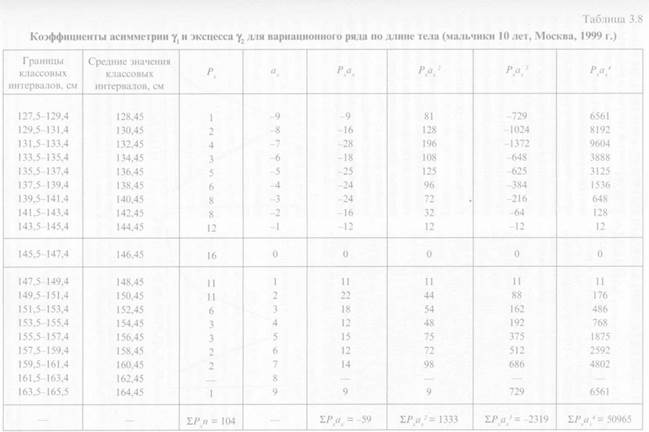
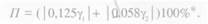
Для нашего примера погрешность П = [(0,125- 0,02) + (0,058- (-0,03)] 100% = 0,42%.

Коэффициенты асимметрии и эксцес­са для данного вариационного ряда, а так­же погрешность (П<5%) показывают, что отклонения эмпирического ряда от нормаль­ного несущественны (см. приложение 6).

Таким образом, зная коэффициен­ты асимметрии и эксцесса исследуемых антропометрических признаков, при построении размерной типологии мож­но определить степень отклонения рас­пределения того или иного признака от нормального и установить, для каких признаков при расчете распределений следует применять метод логарифмичес­кой трансформации [1; 8-10; 15].

Как уже отмечалось, этот метод заключается в том, что с помощью преобразующей функции типа

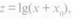
где х₀ = const, распределение, отклоня­ющееся от нормального, можно привести к нормальному виду. Для функции рассчитывается средняя арифметичес­кая величина и среднее квадратичное отклонение в логарифмических едини­цах. Построенная по ним теоретическая кривая нормального распределения хо­рошо согласуется с эмпирическим рас­пределением частот функции. Естествен­но, что симметричная в логарифмической шкале

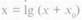
теоретическая кривая (рис. 3.8, а) в абсолютной шкале становится правосторонне-асимметрич-ной (рис. 3.8, б) и учитывает таким об­разом скошенность эмпирического ряда.

Расчеты средних арифметических величин и средних квадратичных откло­нений в логарифмических единицах не­сложны, определенную трудность со­ставляет расчет л_(|.

Расчеты, необходимые для прове­дения логарифмической трансформа­ции, приводятся в приложениях 8-10.

Дата добавления: 2015-06-04