Регрессия (теоретическая и эмпирическая)

Коэффициент корреляции указы­вает на степень связи двух переменных величин, но не дает возможности судить о том, как меняется одна величина по мере изменения другой. Коэффициент, который показывает, как меняется один признак при изменении другого на еди­ницу измерения, носит название коэф­фициента регрессии R. Коэффи­циент регрессии определяется для при­знака х по признаку у по формуле

для признака у по признаку х по фор­муле

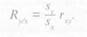
Эти коэффициенты не равны меж­ду собой за исключением случая, когда S_x = S_y

По данным табл. 3.10 можно вычис­лить коэффициент регрессии длины тела по обхвату груди:

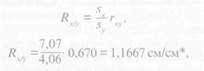
Таким образом, при изменении обхва­та груди на 1 см у мальчиков 10 лет длина тела изменится в среднем на 1,17 см.

Так же можно вычислить коэффици­ент регрессии для обхвата груди по длине тела:

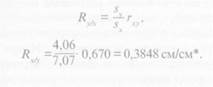
т. е. при изменении длины тела на 1 см об­хват груди изменяется в среднем на 0,38 см.

Путем сравнительно несложных вычислений можно определить среднее значение одного признака по заданно­му значению другого признака. Для это­го надо составить уравнение регрессии. Оно имеет вид уравнения прямой линии

Графически такого рода связь вы­ражается прямой линией.

Так, например, уравнение регрессии обхвата груди по длине тела для нашего при­мера (таблица 3.10) будет иметь вид:

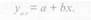
Известно, что х_x = 145,31 см. х_y = 72,29см, s_x = 7,07 см, s_y = 4,06 см, r_xy= 0,670; R_x/y= 0, 3848 (см. таблицу 3.10).

Необходимо найти коэффициенты уравнения регрессии а и b.

В нашем примере коэффициент b ра­вен R_x/y = 0, 3848; коэффициент a =y-bx; а= 72, 29-145, 31 • 0,3848 = 16, 3747 см**.

Таким образом, уравнение регрессии будет иметь вид:

По результатам решения этого уравнения можно построить график. Для этого следует рассчитать обхват груди для двух любых заданных длин тела. На рис. 3.11 представлены эмпирическая 1 и теоретическая 2 регрессии для обхвата груди по длине тела у маль­чиков 10 лет.

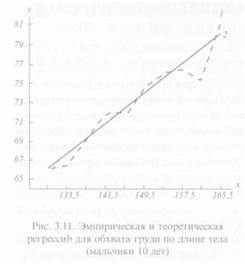
Чтобы установить соответствует ли прямая линия, полученная по теоре­тическому уравнению регрессии, эмпи­рическим данным, рассчитывается эм­пирическая регрессия.

Эмпирическая регрессия — это средние значения одного признака, вычисленные по эмпирическим данным, в каждом классовом интервале по дру­гому признаку.

Эмпирическая регрессия вычис­ляется по формулам

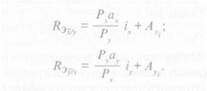
где i_x i_y — классовые интервалы; А_xi А _yi -средние значения классовых интервалов.

Найдем для данного примера эм­пирическую регрессию обхвата груди у по длине тела х у мальчиков 10 лет.

Результаты вычисления обхвата груди у по заданным длинам тела х (эм­пирическая и теоретическая регрессия) представлены в табл. 3.13.

В первую графу таблицы выписывают средние значения классовых интервалов по длине тела, во вторую графу — численность в каждом классовом интервале Р_х, в третью графу — численность по обхвату груди в каждом классовом интервале по длине тела, умноженную на условные отклонения обхва­та груди Р_yа_y. Далее в четвертой графе зна­чения Р_yа_y в каждом классовом интервале по длине тела делят на значения Р_x. Так. в интервале, где среднее значение 129,45 см, Р_yа_y/Р_x = -15/3 = -5,00, в следующем интер­вале — Р_yа_y / P_x = -34/7 = -4,86 и т. д. В пятой графе данные, полученные в четвертой гра­фе Р_yа_y /P_x, построчно умножают на величи­ну классового интервала по обхвату груди (по табл. 3.10 i = 1,5 см).

Эмпирическую регрессию Rэ — ряд обхватов груди для каждого класса длин тела (графа шестая) — получают построч­ным вычитанием данных пятой графы Р_yа_y / P_x • i_yиз условного среднего оохвата

груди (71,45 см).

В первом интервале будем иметь: 73,7-7,5=66,20 см, в следующем интер­вале: 73,7- 7,29 = 66,41 см.

Для этих же длин тела следует рассчи­тать теоретическую регрессию R, по урав­нению прямой линии. Обе линии наносят на график, на котором по оси абсцисс откла­дывают длину тела, а по оси ординат - об­хват груди (см. рис. 3.11). Как видно из ри­сунка, обе линии достаточно хорошо согла­суются.

По уравнению регрессии можно определить зависимость среднего значе­ния одного признака одновременно от двух и более других признаков. Напри­мер, при нахождении среднего обхвата бедер для заданных обхватов груди и об­хватов талии применяют уравнение множественной регрессии типа у = а+bх₁+сх₂.

Таблица 3.13

Дата добавления: 2015-06-04