Задачи для самостоятельного решения. Задача 2. Найти основные парамет­ры х` и s для вариационною ряда, состав­ленного в задаче 1

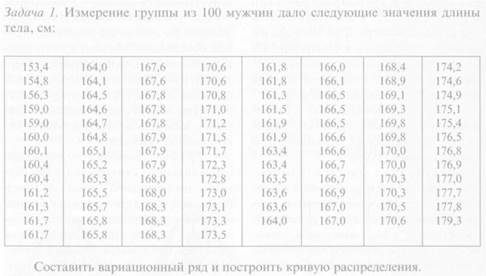
Задача 2. Найти основные парамет­ры х` и s для вариационною ряда, состав­ленного в задаче 1.

Задача 3. Вычислить х` и s длины тела при n=200, ∑Р_x а_x = 103, ∑Р_x а_x²= 1371, если классовый интервал, в котором находится условная средняя, равен 157,5-159,4 см.

Задача 4. Найти общую среднюю арифметическую величину длины тела трех групп, если х`₁ = 157,55 см, n₁=200; х₂= 158,04 см, n₂=300; x₃= 159,02 см, п₃= 150.

Задача 5. Пользуясь таблицами ординат нормальной кривой, рассчи­тать нормальное распределение для сле­дующего вариационного ряда:

Нанести на график эмпирические и теоретические значения.

Задача 6. Рассчитать численность людей, имеющих обхват груди в интер­вале 92-104 см при x`=95,6 см, s=7.2 см.

Задача 7. Рассчитать, чему равно среднее квадратичное отклонение об­хвата талии, если минимальное значе­ние признака 53 см, максимальное — 16 см (размах изменчивости равен 6s).

Задача 8. Средняя арифметическая величина обхвата груди 96,5 см, среднее квадратичное отклонение — 7,5 см. В каких пределах лежат 45; 86,6; 99,95% всех случаев этой выборки?

Задача 9. Определить размах из­менчивости длины тела в группе муж-чип, если средняя арифметическая вели­чина х = 170,4 см; s= 6,1 см.

Задача 10. Найти, какова будет от­носительная численность людей с длиной тела от 168,5 до 169,5 см, если средняя арифметическая величина длины тела для данной группы 168 см, a s = 6 см.

Задача 11. Определить в каких пределах находятся средняя арифмети­ческая величина и среднее квадратич­ное отклонение обхвата груди в гене­ральной совокупности если х выбор­ки = 96,5 см, s = 7,5 см, п = 1000 чело­век.

Задача 12. Установить достовер­ность различия средних арифметичес­ких величин но росту в двух выборках, если x₁ = 156,85 см, s₁ = 5,80 см, п₁ = 500; х₂= 155,45 см, s₂ = 5,70 см, n₂ =500.

Задача 13. Установить достовер­ность различия средних арифметичес­ких величин обхвата груди, если х. = 98,05 см, s₁ = 5,77 см, n₁ = 200;x₂ = 98,75 см,s₂ = 6,36 см, n₂= 100.

Задача 14. Определить достовер­ность различия обхвата груди для тех же выборок, что и в задаче 13, если числен­ность каждой выборки составляет 600 человек.

Задача 15. По уравнению регрессии определить, на какую величину изменя­ется длина руки x₁ при увеличении длины тела x₂ на 6 см и обхвата груди х₃ на 4 см:

x₁= -2,40 + 0,32x₂ + 0,12x₃

Задача 16. По уравнению регрессии определить ширину груди х₁ для чело­века с длиной тела x₂ = 170 см и обхва­том груди х₃ = 96 см:

x₁ = 3,96 + 0,04x₂ + 0,26x₃.

Задача 17. Определить частные средние квадратичные отклонения s'_x/y и s'_y/x и длины тела x и обхвата груди у, если

s_x = 6,08 см, s_y = 9,40 см, r_xy = 0,100.

Задача 18. У 25 измеренных 11-лет­них мальчиков получены следующие значения ряда антропометрических при­знаков, см:

В горизонтальных строчках нахо­дятся значения признаков, полученные при измерении одного и того же чело­века.

Пользуясь приложением 2, найти основные статистические параметры х и s для каждого из этих признаков.

Пользуясь приложением 12, опре­делить следующие коэффициенты кор­реляции: r_x1x2, r_x1x3, r_x1x4, r_x1x5, r_x1x6, r_x1x7, r_x6x7

Дата добавления: 2015-06-04