Расчет кривой нормального распределения по ординатам нормальной кривой

ЗАКОНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ ЧАСТОТ ВАРИАНТОВ АНТРОПОМЕТРИЧЕСКИХ ПРИЗНАКОВ

Анализ вариационных рядов ант­ропометрических признаков позволяет отметить общую закономерность в рас­пределении численностей, которая за­ключается в том, что крайние значения размеров тела встречаются значительно реже, чем средние или близкие к ним значения.

Для решения задач антропометри­ческой стандартизации необходимо обобщить повседневные наблюдения и выразить эту закономерность в количе­ственной форме, т. е. изучить, сколько и каких вариантов величин каждого признака встречается во всей совокуп­ности, и научиться предсказывать эти цифры на основе изучения ограничен­ной выборки.

Область математики, которая с помощью формул (или математических моделей) дает возможность описывать и сопоставлять ряды распределения ча­стот, носит название теории вероятно­стей.

Понятию «частота встречаемости признака» в математике соответствует понятие «вероятности» (под вероят­ностью понимается возможность прояв­ления того или иного события).

Теория вероятностей, основываясь на данных, полученных на практике, создает такие теоретические распределе­ния частот или вероятностей, которые служат для описания реально встреча­ющихся в природе распределений. Од­ним из таких распределений является нормальное распределение.

Нормальное распределение отображает сложность и многообра­зие условий, влияющих на изменчи­вость признаков. Основные свойства нормального распределения следую­щие:

1) на величину признаков влияет множество факторов (например, длина тела человека зависит как от наслед­ственных факторов, так и от условий, в которых протекает рост и развитие организма в отдельные возрастные пе­риоды);

2) степень влияния каждого отдель­ного фактора невелика;

3) действия всех факторов сумми­руются;

4) влияние многочисленных и не­зависимых друг от друга факторов при совокупном действии приводит к нор­мальному распределению.

Нормальное распределение охва­тывает широкий круг явлений как в природе, так и в технике * [3-6; 15].

Еще во второй половине прошло­го столетия бельгийский антрополог А. Кетле (1796-1874 г.) заметил приме­нимость закона нормального распреде­ления к антропометрическим призна­кам. По отношению к ним закон нор­мального распределения может быть сформулирован так: различные вариан­ты признаков в любой неподобранной группе населения одного пола и возрас­та встречаются с различной частотой — средние и близкие к ним значения встре­чаются наиболее часто, по мере удале­ния от средней арифметической величи­ны частота встречаемости признака уменьшается [1; 5; 6; 15].

Таким образом, нормальное распределение представляет собой определенную функциональную зависи­мость между величиной признака и его частотой в совокупности. Эта зависи­мость, как и многие функциональные зависимости между двумя переменными, может быть выражена в табличной фор­ме, графически и при помощи формулы.

Графически закон нормального распределения выражается симметрич­ной, одновершинной плавной кривой, называемой кривой нормального рас­пределения, или просто нормальной кривой**.

Уравнение нормальной кривой имеет вид

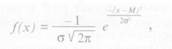
где f(x) — частота встречаемости признака (относительная численность); М — средняя арифметическая величина: σ и σ²— среднее квадратичное отклонение и дисперсия при­знака, характеризующие степень его измен­чивости;,\' — переменное значение призна­ка; е — основание натурального логарифма, равное 2,71828; к — постоянное число, рав­ное 3,14159.

Если принять σ = 1 и вместо

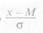
подставить и, то уравнение нормальной кривой примет вид

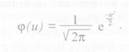
В таком виде уравнение носит на­звание функции нормированного отклонения φ (и), которую можно рассчитать для любых значений и.

Таблицы значения φ (и) обычно называются таблицами ординат кри­вой нормального распределения.

Исходя из уравнений кривой нор­мального распределения и зная, чему равна средняя арифметическая величи­на и среднее квадратичное отклонение, по таблицам ординат можно рассчитать теоретическую кривую нормального распределения для любого эмпиричес­кого ряда. Чтобы пользоваться табли­цами, необходимо выразить значение признака в виде отклонений от средних арифметических величин, деленных на свои средние квадратичные отклонения:

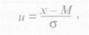
где и — нормированное отклонение; х - М — отклонение середины значений классовых интервалов от средней арифметической ве­личины; σ — среднее квадратичное откло­нение.

Такая операция называется норми­рованием.

Кривую нормального распределе­ния рассчитывают следующим образом:

1) находят отклонения среднего значения каждого классового интерва­ла от средней арифметической величи­ны (х — М)\

2) вычисляют нормированные от­клонения для каждого классового ин­тервала;

3) по таблицам ординат нормаль­ной кривой (см. приложение 3) находят φ (и) (с округлением до четвертого зна­ка);

4) теоретическую численность на­ходят по формуле

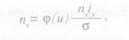
где п₁ — эмпирическая; f — классовый ин­тервал.

Допустим, что надо рассчитать тео­ретическую кривую нормального рас­пределения для эмпирического вариационного ряда по длине тела женщин.

Средняя арифметическая величина для данного вариационного ряда М = x^-=158,42 см, среднее квадратичное от­клонение σ = s = 5,16 см, численность n - 210, классовый интервал i_x = 3 см. Расчет кривой нормального распределе­ния представлен в табл. 3.6.

После расчета эмпирическую б и теоретическую а кривые наносят на гра­фик (рис. 3.3). где по оси абсцисс откла­дывают абсолютные значения призна­ка от минимума до максимума (средние значения классовых интервалов), по оси ординат — частоту встречаемости ири-шака. Из графика видно, что теорети­ческая кривая а расположена симмет­рично относительно вертикали, прове­денной через среднюю арифметическую величину. Средняя арифметическая ве­личина, медиана и мода в кривой нормального распределения совпадают (рис. 3.4).

Ветви кривой асимптотически при­ближаются к оси абсцисс.

Как видно из формулы, в нормаль­ном распределении между средним квад­ратичным отклонением о и частотой встречаемости вариантов признака в совокупности имеется функциональная зависимость. Эта зависимость позволя­ет определить относительную числен­ность случаев, заключенных в любом заданном интервале значений признака. Для этого достаточно знать среднее арифметическое значение признака в данной совокупности и его среднее квад­ратичное отклонение. Вычислив норми­рованные отклонения заданных границ интервала от средней арифметической величины М, по таблицам площадей (интегралов) нормальной кривой мож­но определить относительные численно­сти, заключенные в заданных границах.

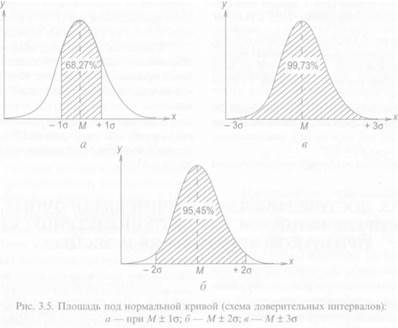
Для примера выпишем из таблиц площадей (см. приложение 4) несколь­ко соотношений, которые можно изоб­разить и графически (рис. 3.5). Оказы­вается, что при нормальном распреде­лении признака в пределах М ± 0,67 σ укладывается 50% случаев в пределах М ± 1 σ — 68,27% (см. рис 3.5, и). В преде­лах М ± 2 σ заключено 95,45% (см. рис. 3.5, б) и в пределах М ± З σ — 99,73% случаев (см. рис. 3.5, в).

Можно записать и обратные соот­ношения. Например, можно утверж­дать, что 95% случаев лежит в пределах М ±1. 96 σ 99% случаев — в пределах •М ± 2,58 σ и 99,9% случаев — в преде­лах М ± 3.29 σ. Практически вся сово­купность заключена в пределах М ± 3,5а. Значения признаков, выходящие за эти пределы (при наличии нормального рас­пределения), следует считать нетипич­ными для данной совокупности (см. при­ложение 4).

Таблица 3.6

В математической статистике при оценке результатов измерений принято пользоваться определенными частями площади кривой нормального распре­деления, а именно: 95, 99, 99,9%. Веро­ятности 0,95, 0,99 и 0,999 получили на­звание доверительных вероятнос­тей*. Каждая из этих вероятностей со­ответствует определенным границам, а именно: М± 1,96 σ, М± 2,58 σи М+ 3,29 σ соответственно. Интервалы, заключен­ные в этих пределах, называются дове­рительными интервалами для среднего значения признака. Довери­тельный интервал показывает границы, в которых с той или иной вероятностью заключена искомая величина⁴ [3].

Например, если средний рост муж­чин 167 см, среднее квадратичное откло­нение 6 см, то можно утверждать с ве­роятностью 0,99, что у первого встре­ченного нами человека рост будет не ниже 151,5 см и не выше 182,5 см, так как 167-(6-2,58 σ )=151,52 см и 167+(6-2,58 σ )=182,48 см.

Разберем несколько примеров при­менения закона нормального распреде­ления антропометрических признаков для решения конкретных задач.

Пример 1. Средняя арифметическая величина длины тела для группы мужчин М = х = 168 см, среднее квадратичное от­клонение σ = s = 5 см.

Определить, в каких пределах заклю­чено 45, 86,6 и 99,95% случаев этой совокуп­ности.

В приложении 4 находим, что 45% всех случаев находится в пределах М ± 0,6 σ. Сле­довательно, х ± 0,6 • 5 = (168 ±3) см, т. е. 45% людей в данной совокупности имеют длину тела от 165 до 171 см; 86,6% — в пределах М ± 1,5 σ, т. е. 86,6% людей в данной сово­купности имеют длину тела от 160,5 до 175,5 см; и, наконец, 99,95% — в пределах М ± 3,5 σ, т. е. минимальным и максимальным значениями длины тела в данной совокуп­ности будут соответственно 151.5 и 184,5 см.

Пример 2. Определить, какова относи­тельная численность людей в данной выбор­ке с обхватом груди от 100 до 104 см, если средняя арифметическая величина х =96 см и s = 4 см.

Минимальное изданных значений (100 см) отстоит от средней арифметической ве­личины (96 см) на 4 см (d₁, максимальное (104 см) —на 8 см (d₂).

В пределах от средней арифметической величины до минимального значения при­знака укладывается +lσ (s:d₁) в нашем при­мере 4: 4 = +1σ), или 34,1% случаев.

В пределах от средней арифметической величины до максимального заданного зна­чения признака укладывается +2σ (s: d₂, в нашем примере 8:4 = +2σ), или 47,7% слу­чаев.

Следовательно, относительная числен­ность людей с обхватом груди от 100 до 104 см в данной выборке будет составлять 47,7% -34,1% = 13,6%.

Дата добавления: 2015-06-04