Корреляция между антропометрическими признаками

Известно, что у людей одного рос­та все другие размерные признаки могут быть различными. Однако между признаками может быть отмечена определенная связь. Так, у людей с большим обхватом груди большие обхваты талии и бедер будут встречаться чаще, чем маленькие. Можно сказать также, что у невысоких людей небольшие обхваты груди наблюдаются чаще, чем у высо­ких. Вместе с тем при одном и том же обхвате груди люди могут иметь различ­ную длину тела и очень разные обхва­ты талии и бедер. Связь признаков, при которой каждому определенному значению од­ного признака может соответствовать не одно значение второго признака, а целое распределение этих значений, на­зывается стохастической (корре­ляционной) связью, или корреляцией. Причина того, что между ант­ропометрическими признаками суще­ствует корреляция, заключается в том, что организм человека развивается под действием очень большого числа фак­торов, которые по-разному определяют развитие признаков и их связь друг с другом. Корреляция не предполагает точную зависимость одного признака от другого, поэтому эта связь может иметь различную степень тесноты. Так, например, очень тесно связаны между собой длиннотные размеры тела, а так­же обхватные. В качестве примера ма­лой степени тесноты корреляции мож­но привести зависимость между длиной тела и обхватом груди.

Кроме того, характер корреляции между признаками может быть различ­ным, т. е. с увеличением одного призна­ка другой признак может либо увеличи­ваться, либо уменьшаться. В первом слу­чае корреляция будет положительной, или прямой, во втором — отрицатель­ной, или обратной. Большинство антро­пометрических признаков связано меж­ду собой положительной корреляцией. В качестве примера отрицательной кор­реляции можно привести связь обхватных размеров с глубинами позвоночни­ка. С увеличением обхватов некоторые глубины уменьшаются.

Статистическую степень тесноты корреляции между признаками харак­теризует коэффициент корреля­ции r.

Формула для вычисления коэффи­циента корреляции [3; 4]

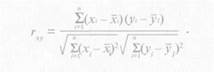
Как видно из этой формулы, в чис­лителе — сумма произведений отклоне­ний каждого из признаков от своих средних арифметических величин, а в знаменателе — произведение средних квадратичных отклонений каждого из признаков. Таким образом, коэффициент корреляции есть не что иное, как средняя сумма произведений норми­рованных отклонений* двух при­знаков:

Нормированные отклонения обла­дают рядом математических свойств [3]. Так, среднее значение суммы произве­дений нормированных отклонений ко­леблется от 0 до 1.

При полном отсутствии связи меж­ду двумя исследуемыми признаками средняя сумма произведений нормиро­ванных отклонений равна нулю, т. е. ∑t_xt_y /п = 0, а при функциональной свя­зи— единице, т. е. ∑t_xt_y /п = 1. Причем, если с увеличением одного признака другой признак будет увеличиваться, средняя сумма произведений нормиро­ванных отклонений будет иметь знак плюс, если уменьшаться — знак минус.

Так как средняя сумма произведе­ний нормированных отклонений и есть коэффициент корреляции, показываю­щий степень тесноты корреляции меж­ду двумя признаками, то можно заклю­чить, что при положительной связи он колеблется от 0 до +1, при отрицатель­ной - от 0 до -1.

Коэффициент корреляции, равный + 1 или -1, будет получен, если одному значению одного признака соответству­ет лишь одно значение другого призна­ка. Практически такого рода связь при исследовании антропометрических при­знаков не встречается.

Условно о большой степени тесно­ты корреляции (связи) можно говорить, если коэффициент корреляции изменя­ется от ± 0,750 до ± 0,999, о средней связи — от ± 0,450 до ± 0,749 и о ма­лой — от 0 до ± 0,449. При коэффициенте корреляции, равном нулю, корреляция между признаками отсут­ствует [3-5].

Так как среднее произведение нор­мированных отклонений есть величина неименованная, то и коэффициент кор­реляции между двумя признаками выра­жается неименованной величиной.

Исходя из общей формулы коэф­фициента корреляции, можно заклю­чить, что практически он представляет собой сумму индивидуальных отклоне­ний от средних арифметических величин одновременно по двум признакам. Вы­числение коэффициента корреляции по общей формуле весьма трудоемко, по­этому, так же как и при вычислении ос­новных статистических параметров, пользуются способом моментов.

Помимо степени тесноты корреля­ции и ее направления определяют фор­му корреляции —прямолинейную и криволинейную.

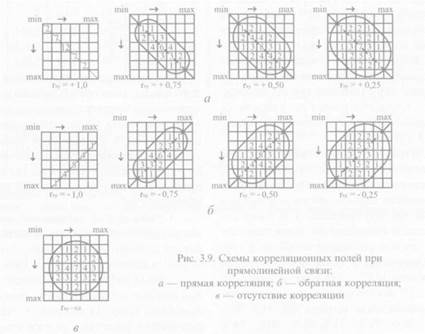
Прямолинейная корреля­ция — это такая связь, при которой равномерным изменениям первого при­знака соответствуют равномерные изме­нения второго признака (рис. 3.9).

При криволинейной корре­ляции равномерным изменениям пер­вого признака соответствуют неравно­мерные изменения второго, причем эта неравномерность имеет определенную закономерность (рис. 3.10).

Степень тесноты корреляции мо­жет быть определена не только между двумя, но и одновременно между тремя, четырьмя и т. д. признаками. В этом слу­чае применяется коэффициент мно­жественной, или совокупной кор­реляции.

Его формула для трех признаков имеет вид

Как видно из формулы, коэффи­циент множественной корреляции опре­деляется через коэффициенты корреля­ции между отдельными парами призна­ков. Коэффициент множественной кор­реляции применяется при расчете ант­ропометрических стандартов (см. гл. 4).

Для расчета коэффициента корре­ляции по способу моментов составляют так называемую корреляционную ре­шетку. Пусть надо вычислить коэффи­циент корреляции между длиной тела и обхватом груди (табл. 3.9) у мальчиков.

По каждому признаку составляют вариационный ряд, для чего находят минимальное и максимальное значения каждого признака, классовый интервал, границы и средние значения классовых интервалов способами, описанными выше.

Корреляционная решетка длины тела x и обхвата груди у приведены в табл. 3.10.

В графах 1 и 2 табл. 3.10 указаны классовые интервалы 1_х и их средние значения 1_хс; в графе 18 -численность P_x в каждом классе по длине тела х (клас­совый интервал i_x = 2 см).

В графах 3-17 указаны классовые интервалы I_y и их средние значения I_{y cp}; по признаку у (обхвату груди); числен­ность в каждом классе по признаку у указана в строке Р_y (классовый интер­вал i = 1,5 см).

У

Чтобы определить степень тесноты корреляции между двумя признаками, прежде всего находят, как распределяют­ся значения одного признака в каждом классе другого признака, т. е. в каждом классовом интервале по длине тела сле­дует сделать раскладку по обхвату гру­ди. Например, в классовом интервале длин тела 143,5 - 145,4 см численность ра в на 12; для указа иных длин тела имеем следующие обхваты груди 70,0; 74,6; 70.4; 69,3; 70,0: 71,8; 71,8; 71.3; 70,0; 74,3; 69,8; 71,9(см. табл. 3.9).

Разложив эти значения в порядке возрастания, имеем:

Итак, в интервале длин тела 143,5 -145,4 см значения обхвата груди распо­лагаются так:

То же следует выполнить для каж­дого класса длин тела. Причем в корре­ляционную решетку следует вносить лишь конечные результаты расчетов (см. табл. 3.10). Таким путем будет по­лучено как распределение обхватов гру­ди в каждом классе длин тела, так и рас­пределение длин тела в каждом классе обхватов груди.

Сумма цифр, записанная в клет­ках корреляционного поля, должна рав­няться общему числу случаев, или вы­борке (в данном примере — 104).

Сумма цифр в каждом классе дол­жна совпадать с численностью итоговых рядов (см.графу 18 и строку Р_y корре­ляционной решетки) по каждому от­дельному признаку.

Длина тела и обхват груди, см (мальчики 10 лет)*

Таблица 3,9

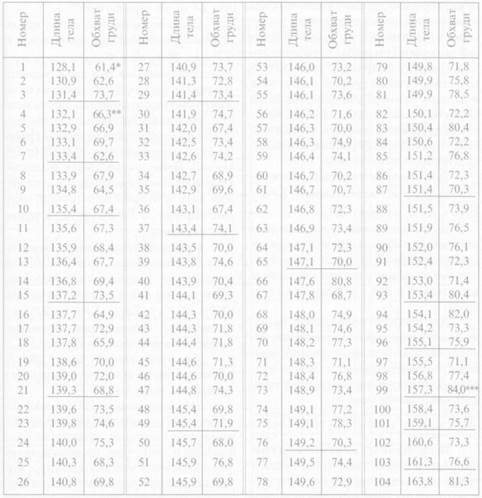
Далее следует найти условные от­клонения каждого из признаков от сво­их условных средних величин, т. е. за­менить средние значения классовых ин­тервалов признака х и признака у услов­ными отклонениями от условной сред­ней величины (см. табл. 3.5) и записать их в графу 19 и строку а табл. 3.10. В качестве условной средней длины тела в данном примере выбрано значение 146,4 см, обхвата груди — 73,7 см. Клас­совые интервалы, в которых находятся выбранные условные средние величины, следует выделить (см. табл. 3.10).

Затем заполняют графы 20 и 21, строку Р_yа_y² и подсчитывают ∑ Р_ха_х, ∑ Р_ха_x², ∑ Р_yа_y и строку ∑ Р_yа_y².

Далее надо вычислить, насколько отклоняются обхваты груди в условных единицах от своей условной средней ве­личины в каждом классовом интервале длин тела, т. е. Р_yа_y, записать это в гра-фу 23.

Для удобства вычислений на от­дельный бланк переносят условные от­клонения а_y от условной средней вели­чины по обхвату груди, т. е. делают под­вижную шкалу в масштабе граф табл. 3.10 следующего вида:

Передвигая эту шкалу по корреля­ционной решетке так, чтобы нулевая точка шкалы всякий раз соответство­вала нулевому классу у (73,0-74,4), вы­числяют суммы произведений численностей по обхвату груди с учетом зна­ка (табл. 3.11).

Произведения подсчитывают для каждого классового интервала. В кор­реляционную решетку записывают ито­говую величину Р_yа_y (графа23) для каждого классового интервала длин тела.

Следующий этап — вычисление суммы этих отклонений, т. е. определе­ние ∑ Р_yа_y по горизонтали.

После этого находят сумму произ­ведений отклонений двух признаков, т. е. ∑ Р_yа_yа_х. Для этого обхваты груди в ус­ловных единицах в каждом классовом интервале длин тела умножают на вели­чину условных отклонений длины тела, т. е. умножают построчно цифры гра­фы 23 по горизонтали на цифры графы 20. Итоги записывают в графу 24 (пост­рочно). Просуммировав эти значения, получают сумму произведений отклоне­ний двух признаков от условных сред­них величин — ∑ Р_yа_yа_х = 722 в услов­ных единицах.

Прежде чем переходить к вычисле­нию основных параметров каждого из признаков и степени связи между при­знаками, все ранее найденные суммы ( ∑ Р_ха_х, ∑ Р_ха_х², ∑ Р_yа_y, ∑ Р_yа_y² и ∑ Р_yа_yа_х) проверяют, т. е. делают так называемую косую проверку решетки (табл. 3.12).

Для этого следует найти ряд Р, суммируя частоты по диагоналям (как показано в табл. 3.10).

На корреляционной решетке для облегчения последующих расчетов про­водят три основные диагонали: две крайние и диагональ, проходящую че­рез пересечение нулевых классов х и у, однако расчет производят по всем диа­гоналям решетки. Так, в первых пяти диагоналях нашей решетки получены следующие численности:

Дата добавления: 2015-06-04