Приведение системы сил к центру

Используя правило приведения силы к заданному центру, сложим три произвольно расположенные силы в пространстве см. рис. 51а.

Дано: Первая сила 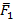действует в плоскости Oxz, плоскости 1 из точки А. Вторая сила 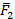действует в плоскости Oxy, плоскости 2 из точки В. Третья сила действует в плоскости Oyz, плоскости 3 из точки С.

Задание. Привести заданные силы к точке О.

Решение. Приводим силу 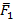к заданному центру. В начале параллельно перенесем ее в новый центр. Для определения вектора момента первой силы относительно точки О проведем плоскость через радиус-вектор и вектор силы 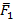, получим заштрихованную плоскость, как показано на рис. 51а, рис. 51б. К этой плоскости из точки О нужно провести перпендикуляр, на котором находится вектор момента первой силы. Направление вектора момента находится по правилу буравчика – в нашей схеме вектор момента первой силы лежит на оси у в положительном направлении. Запишем:

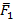
1. 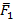перенесем параллельно в новый центр, точку О. Добавим момент этой силы относительно точки О

Приводим силу 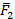к заданному центру. Также параллельно перенесем ее в новый центр. Для определения вектора момента второй силы относительно точки О проведем плоскость через радиус-вектор 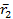и вектор силы 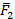, получим заштрихованную плоскость, как показано на рис. 51. К этой плоскости из точки О нужно провести перпендикуляр, на котором находится вектор момента второй силы. Направление вектора момента находится по правилу буравчика – в нашей схеме вектор момента второй силы лежит на оси z в отрицательном направлении. Запишем:

2. 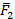перенесем параллельно в новый центр, точку О. Добавим момент этой силы относительно точки О

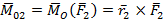
Приводим силу 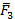к заданному центру. Также параллельно перенесем ее в новый центр. Для определения вектора момента третьей силы относительно точки О проведем плоскость через радиус-вектор 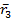и вектор силы 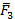, получим заштрихованную плоскость, как показано на рис. 51. К этой плоскости из точки О нужно провести перпендикуляр, на котором находится вектор момента третьей силы. Направление вектора момента находится по правилу буравчика – в нашей схеме вектор момента

третьей силы лежит на оси х в положительном направлении.

3. 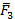перенесем параллельно в новый центр, точку О. Добавим момент этой силы относительно точки О

4. В точке О получили систему трех сходящихся сил

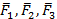, (см. рис. 51а, б). Приводим систему трех сил к равнодействующей, которая называется главным вектором системы трех сил (см. рис. 52а).

, т.е. , где k=1,2,3

В общем случае главный вектор системы сил равен

, (1)

где k=1,2,….,n.

5. В точке О получили систему трех сходящихся векторов моментов сил 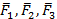, (см. рис. 51б). Приводим систему трех векторов моментов сил к равнодействующей, которая называется главным вектором- моментом всех сил или момент главной пары (см. рис. 52б).

,

,

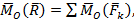
где k=1,2,3.

В общем случае главный вектор-момент или момент главной пары равен

(2)

где k=1,2,….,n.

Рис. 51

Рис. 52

Вывод. Приведение произвольной системы сил, действующих на объект, к заданному центру по правилу Пуансо дает результат –

1. Главный вектор системы сил равен векторной сумме сил. действующих на объект, определяется по формуле:

, (1)

где k=1,2,….,n.

2. Вектор главного момента всех сил относительно заданного центра или вектор-момент главной пары, действующих на объект, определяется по формуле:

(2)

где k=1,2,….,n.

3. Формулы (1), (2) имеют векторную форму. Их можно представить через координатную форму.

Главный вектор сил можно записать через её проекции:

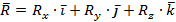, (a)

где 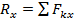, , 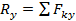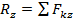(1a). Алгебраическая сумма проекций всех сил на оси x, y, z есть проекции главного вектора на эти же координатные оси и наоборот.

4. Главный момент сил относительно заданного центра или вектор-момент главной пары можно записать через проекции по формуле:

5. 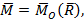где

,

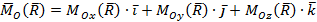или (2а)

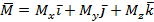
Задание.

Дано:

Тело в форме прямоугольной призмы с заданными размерами.

Известны силы по величине:

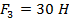
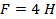
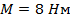
Пара сил с моментом М находиться в горизонтальной плоскости.

Начало каждого вектора силы показано на рисунке.

1. Найти главный вектор заданной системы сил.

2. Найти главный момент системы сил при приведении их к точке О.

3. Найти главный момент системы сил при приведении их к точке А.

4. Найти главный момент системы сил при приведении их к точке В.

5. Найти главный момент системы сил при приведении их к точке С.

6. Найти главный момент системы сил при приведении их к точке Е.

7. Найти главный момент системы сил при приведении их к точке К.

Дата добавления: 2015-06-04