Пара сил и её свойство

Познакомимся с понятием «Пара сил».

Парой сил называются две силы, которые параллельны и противоположно ориентированы, не лежат на одной прямой и равны по модулю (см. рис. 47).

Рис. 47

Пару сил по сути знали, только не знали ее названия. Например, с помощью пары сил открываете ключом дверь, раскручиваете шариковую ручку для замены стержня, сидите за рулем автомобиля, открываете бутылку с водой и т.д. Следовательно, пара сил является моментом. Момент пары сил равен произведению одной из сил на кратчайшее расстояние между ними, взятое со знаком «+» или «-». Правило знаков у моментов такое же, что для момента силы относительно точки и оси: если вращение момента пары сил осуществляется против часовой стрелки, то записывается знак «+» и наоборот (см. рис. 48, рис. 49).

Рис. 48

На рис. 49 на верхней строке показаны пары сил в разных положениях, но в одном направлении; на нижней строке аналогично, но в другом направлении. Значит, действие пары сил можно показать через две силы, а можно через крутящий момент в нужном направлении.

Рис. 49

Если величина момента силы относительно точки зависит от выбора точки, относительно которой рассматривается момент силы, то момент пары сил не зависит от выбора точки. На рис. 45 можно увидеть доказательство того, что момент пары сил не зависит от выбора точки. Например, выбирается точка О на продолжении отрезка АВ, которая перпендикулярна линиям действий сил, составляющих пару. Если записать сумму моментов двух сил пары относительно этой точки О, то получим величину момента пары сил, которая не зависит от выбора точки, а зависит от расстояния между силами и направления пары сил. Вектор момента пары сил перпендикулярен плоскости, где находится пара сил, направление вектора определяется по правилу буравчика: если смотреть на конец вектора момента, то вращение его должно быть против часовой стрелки.

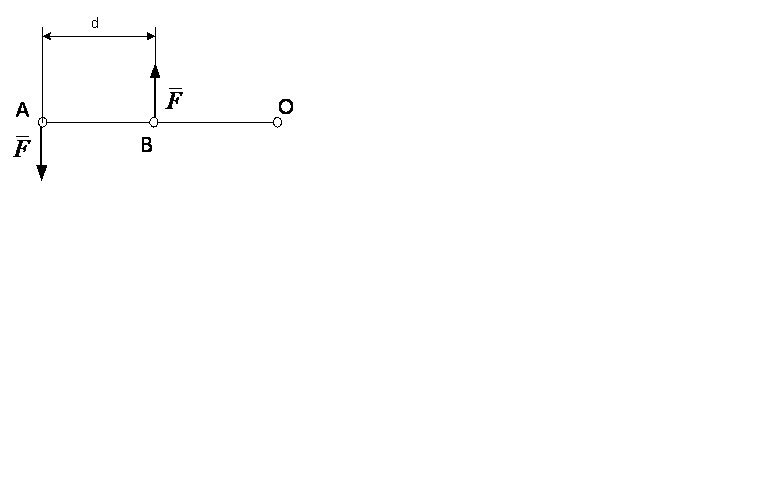
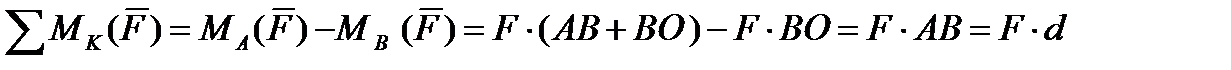
Рис. 45

Свойство пары сил

Рассмотрим свойство пары сил на плоскости.

Теорема 1.

Пару сил можно переносить в плоскости её действия из одного места в другое. Состояние тела при этом не изменится.

Докажем эту теорему. Для этого см. рис. 46.

Дано: пара сил 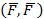с моментом .

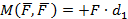Доказать, что данную пару 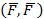с моментом

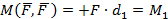можно заменить другой парой сил 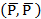с таким же по модулю моментом, т.е.

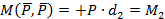или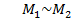

1. Линии действия сил у двух пар пересекутся в точках А и В. К точке А приведем верхние силы 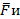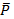первой и второй пар как показано на рисунке 46. К точке В остальные силы этих пар. В точке А результирующую силу 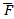разложим на составляющие по правилу параллелограмма, так что 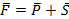. В точке В по аналогии - разложим результирующую силу 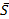на составляющие 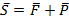. Так что на прямой АВ имеем две уравновешенные силы .

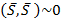3. Обозначим концы векторов сил 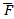и 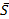в точке А точками а и b соответственно. Рассмотрим два треугольника Aab и ABD. Первый треугольник подобен второму треугольнику: 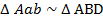по третьему признаку, когда у треугольников вершина А общая, а другие углы равны как соответственные: 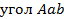равен углу ADB и угол Aba равен углу ABD, поскольку ab параллельна стороне DB из построения, причем ab=P. Отсюда напишем соотношение:

.

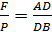4. Опустим перпендикуляры из точки D и точки E на прямые, которые проходят через точки В, Е и DB соответственно. Обозначим точки пересечения перпендикуляров и прямых как точка К и точка L. Рассмотрим теперь треугольники KDB и BEL. Получаем, что эти треугольники подобны по третьему признаку 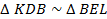, т.к. углы DBK=EBL – как вертикальные и углы DKB=ELB – как прямые, то углы KDB=BEL. Т.к. сумма углов в треугольнике равна 180⁰. Отсюда можно записать

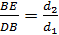, где BE=AD, т.е. можно записать .

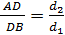5. Выпишем выводы со п.2 и п.3:

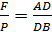и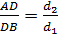

Отсюда 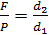или = .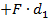

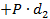Следовательно, пару сил 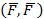с моментом

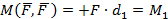.можно заменить

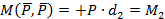и первый момент пары сил

эквивалентен второму моменту второй пары сил:

.

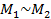Значит, пару сил можно переносить в плоскости её действия в любое место, при этом состояние объекта не изменится (cм. рис. 47).

Теорема 1 доказана.

Рис. 46

Рис. 47

Для того чтобы рассмотреть свойство момента пары сил в пространстве нужно доказать теорему.

Теорема 2.

Пару сил можно переносить в пространстве из одного места тела в другое. Состояние тела при этом не изменится.

Доказательство проведем см. рис. 48.

Рис. 48

Дано: В плоскости 1 тела в пространстве действует пара сил с моментом М₁.

Доказать: вектор момента пары сил есть вектор свободный, т.е. вектор момента пары сил можно переносить в любое место тела, при этом состояние тела не изменится.

1. Проведем плоскость 2, которая параллельна

плоскости 1. Из теоремы 1 момент пары М₁ представим парой сил 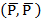с тем же моментом. Обозначим точками А и В кратчайшее расстояние между силами 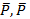в плоскости 1.

2. В плоскости 2 проведем отрезок DC, который параллелен АВ и равный ему. В точках D и С приложим уравновешенные силы: в точке С соответственно 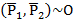и в точке D - 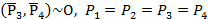=P.

3. Через точки А, В, С, D проведем плоскость, которая пересекает плоскости 1 и 2. Плоскостью является прямоугольник в ней проведем диагонали АС и DВ, точку пересечения диагоналей обозначим точкой О.

4. Приведем к равнодействующим параллельные силы 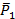и , ; , .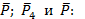

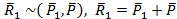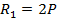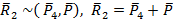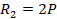5. В точке О имеем уравновешенные силы

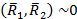, значит, что силы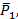 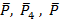представляют уравновешенную систему.

6. Из системы 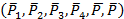шести равных по

модулю и параллельных сил, действующих на систему, остались только две силы 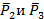, которые представляют собой пару и находятся в плоскости 2.

7. Из сказанного можно сделать вывод: пару сил можно переносить в любое место тела, при этом состояние его не изменится. Значит, вектор момента пары сил есть вектор свободный (см. рис. 48).

Теорема 2 доказана.

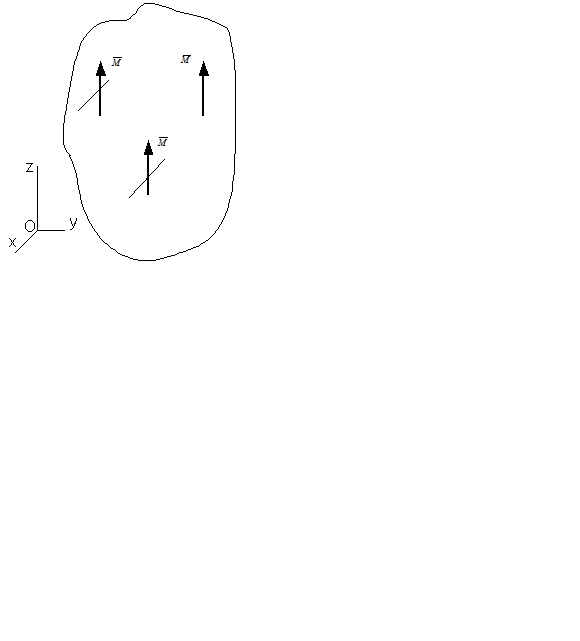
Рис. 48

Сложение пар сил

В плоскости пары сил складываются как алгебраическая сумма с учетом знаков моментов. Вектор результирующего момента перпендикулярен плоскости, где действуют моменты пар сил, может находиться в любом месте. Рассмотрим рис.49. В горизонтальной плоскости действуют моменты трех пар сил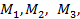

где ,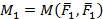

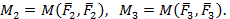
Рис. 49

Пусть 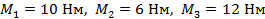. Определить величину и направление результирующего момента пары сил.

Решение: М=+ 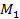+ 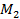- 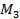=10+6-12=4 (Нм); .

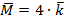В пространстве момент главной пары или результирующий момент находится по правилу треугольника. Как складываются сходящиеся силы: к концу первого вектора момента пары сил прикладывается второй вектор момента пары сил и т.д., затем соединяем начало первого вектора момента пары сил и конец последнего вектора момента пары сил - получаем главный вектор, момент результирующей пары определяется по формуле:

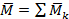, где k=1,2,…,n.

Задание.

1. Определить модуль и направление главной пары, если первый момент пары сил принадлежит горизонтальной плоскости Оху и равен 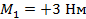, второй момент пары сил действует в плоскости Oxz и равен 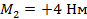, третий момент пары сил действует в плоскости Oyz и равен .

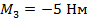2. Объясните состояние тела, если главный момент равен нулю.

3. Чем отличаются между собой пара сил и две уравновешенные силы?

4. Чем отличаются между собой пара сил и момент силы относительно точки?

5. Каким свойством обладает пара сил?

6. Что общего у пары сил и момента силы относительно точки?

7. Есть ли общее у распределенной нагрузки и пары сил?

8. Когда момент пары сил равен нулю?

Дата добавления: 2015-06-04