
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Системы сил и главного момента всех сил
|
|
|
|
Случаи приведения главного вектора
1. РАВНОВЕСИЕ объекта. Состояние объекта является покой или поступательное прямолинейное движение тела.
Главный вектор системы сил, действующих на объект, равен нулю. Главный момент сил, действующих на объект, равен нулю.
 (1)
(1)
(I)
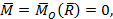 (2)
(2)
где k=1,2,….,n. Формула (I) означает векторную форму записи условия равновесия тела.
Если главный вектор системы сил и главный момент равны нулю, то будет РАВНОВЕСИЕ объекта, а именно равновесие в данный момент времени, поскольку не рассматривается какое именно равновесие: устойчивое или нет. Устойчивое равновесие наблюдается при условии, что потенциальная энергия является минимальной 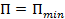 .
.
2. Приведение системы сил к равнодействующей. ПОСТУПАТЕЛЬНОЕ движение тела.
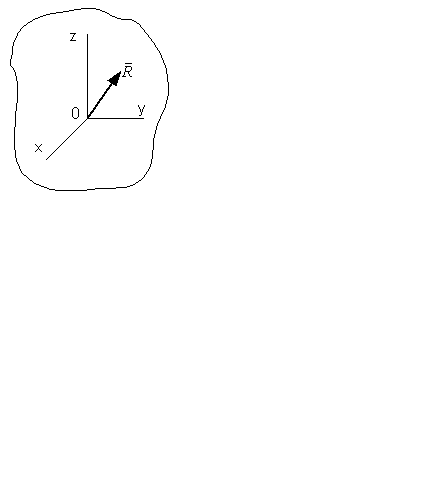 Главный вектор системы сил, действующих на объект, не равен нулю. Главный момент сил, действующих на объект, равен нулю.
Главный вектор системы сил, действующих на объект, не равен нулю. Главный момент сил, действующих на объект, равен нулю.
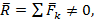 (1)
(1)
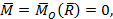 (2)
(2)
где k=1,2,….,n.
Пример. Все точки тела имеют
геометрически равные скорости
и ускорения при его поступательном Рис. 52
движении.
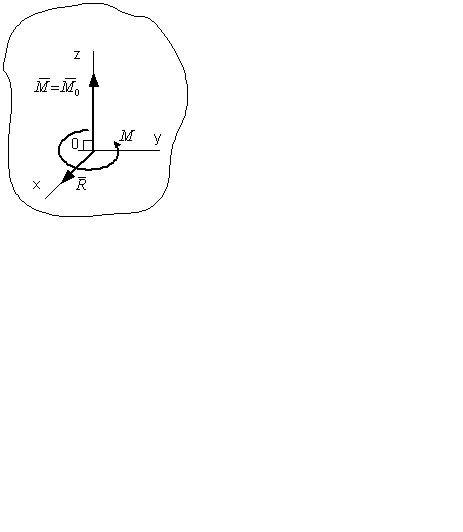
3. Приведение системы сил к паре сил. ВРАЩАТЕЛЬНОЕ движение тела.
Главный вектор системы сил, действующих на объект, равен нулю. Главный момент сил, действующих на объект, не равен нулю.
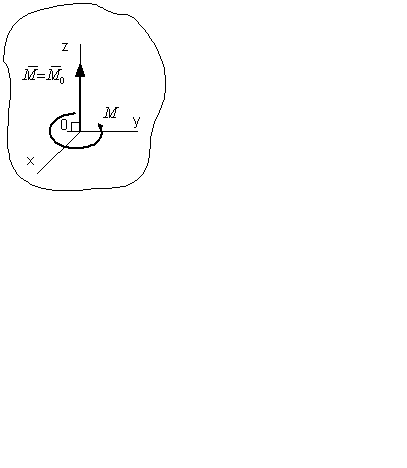
 (1)
(1)
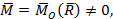 (2)
(2)
где k=1,2,….,n.
Пример. Тело вращается вокруг
неподвижной оси или неподвижной точки. Все точки тела, кроме точки
через которую проходит ось или точки крепления, имеют одинаковые угловые
скорости и ускорения. Рис. 53
4. Приведение системы сил к равнодействующей силе. ПЛОСКОЕ движение тела.
 Главный вектор системы сил, действующих на объект, не равен нулю. Главный момент сил, действующих на объект, не равен нулю. Но главный вектор перпендикулярен главному моменту
Главный вектор системы сил, действующих на объект, не равен нулю. Главный момент сил, действующих на объект, не равен нулю. Но главный вектор перпендикулярен главному моменту 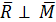 ,
,
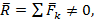 (1)
(1)
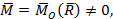 (2)
(2)
где k=1,2,….,n.
Рис. 54
Пример. Движение колеса.
Поступательное движение тела в точке А происходит под действием равнодействующей, проходящей через эту точку, тогда как другие точки тела вращаются вокруг этой
точки. Движение колеса, как плоского тела является плоскопараллельным или плоским.
Рассмотрим подробно этот случай (см. рис. 55). Главный вектор системы сил перпендикулярен к главному моменту 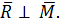 Главный момент является парой сил. Выберем силы пары по модулю равной главному вектору
Главный момент является парой сил. Выберем силы пары по модулю равной главному вектору 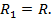 Расположим эту пару так, чтобы одна из сил пары была приложена в точке О и направлена противоположно силе
Расположим эту пару так, чтобы одна из сил пары была приложена в точке О и направлена противоположно силе 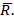 В этом случае силы, лежащие на оси х. являются уравновешенными
В этом случае силы, лежащие на оси х. являются уравновешенными 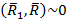 . Остается сила
. Остается сила 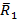 ,линия действия которой проходит через точку А на расстоянии
,линия действия которой проходит через точку А на расстоянии
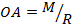 от точки О, причем точка А откладывается так, чтобы смотря навстречу вектора момента
от точки О, причем точка А откладывается так, чтобы смотря навстречу вектора момента 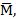 видеть паhe стремящейся вращать плоскость против часовой стрелки.
видеть паhe стремящейся вращать плоскость против часовой стрелки.
Рис. 55
Значит, заданная система сил приводится к равнодействующей силе. Прямая, совпадающая с линией
действия этой силы, называется линией действия равнодействующей силы. Равнодействующая системы сил, приложенная в точке А, эквивалентна заданной системе сил. Главный вектор системы сил в точке О заменяет данную систему только вместе с парой сил с моментом 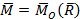 .
.
5. Приведение системы сил к ДИНАМЕ или к двум СКРЕЩИВАЮЩИМСЯ силам.
ВИНТОВОЕ движение тела
Главный вектор системы сил, действующих на объект, не равен нулю. Главный момент сил, действующих на объект, не равен нулю. Но главный вектор не перпендикулярен главному моменту:
,
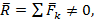 (1)
(1)
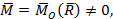 (2)
(2)
А. Случай приведения системы сил к динаме (см. рис. 56 а)
1. Разложим главный момент системы сил на составляющие
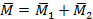 ,
,
где 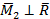 , см. рис. 56 б.
, см. рис. 56 б.
Когда 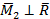 , то такая система приводится к равнодействующей
, то такая система приводится к равнодействующей 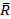 в точке А, как это было рассмотрено в четвертом случае (см. рис.57 а, б, в).
в точке А, как это было рассмотрено в четвертом случае (см. рис.57 а, б, в).
1. Остался не рассмотренным момент 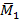 ,
,
Рис. 56 а его вектор параллелен вектору


Рис.56 б Рис. 57 а


Рис. 57 б Рис.57 в
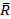 (см. рис. 58 а). Так как вектор момента
(см. рис. 58 а). Так как вектор момента 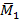 является вектором свободным, то его можно перенести в точку А, где находится результирующий вектор
является вектором свободным, то его можно перенести в точку А, где находится результирующий вектор 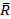 (см. рис. 58 б). Получили ДИНАМУ- одновременное поступательное
(см. рис. 58 б). Получили ДИНАМУ- одновременное поступательное
движение тела (его движение по центральной оси) и вращение его вокруг этой оси, проходящей через линию действия равнодействующей 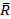 и точку А.
и точку А.
Совокупность силы 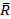 и пары сил
и пары сил 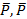 с моментом
с моментом 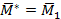 , расположенной в плоскости, перпендикулярной линии действия этой силы, называют силовым винтом или динамой.
, расположенной в плоскости, перпендикулярной линии действия этой силы, называют силовым винтом или динамой.
Линия действия силы 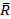 в точке А является центральной осью, как.результат приведение заданной системы сил к динаме в этой точке. Отсюда центральная ось системы сил представляет собой геометрическое место точек пространства, относительно которых главные моменты заданной системы сил имеют наименьший модуль
в точке А является центральной осью, как.результат приведение заданной системы сил к динаме в этой точке. Отсюда центральная ось системы сил представляет собой геометрическое место точек пространства, относительно которых главные моменты заданной системы сил имеют наименьший модуль 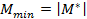 и направлены вдоль этой оси.
и направлены вдоль этой оси.
а б


Рис. 58
Примером может быть работа с дрелью, когда нужно выполнить отверстие, например, в стене: давим на дрель, сверло одновременно движется поступательно в нужном направлении и вращается, продвигаясь до нужного размера. Или другой пример: завинчивание самореза для крепления деталей. Такое движение называется винтовое движение, которое, например, присутствует в прессах, домкратах, когда с помощью небольшого усилия при винтовом движении винта можно поднять или изменить заготовку до нужной формы.
Б. Случай приведения системы сил к двум скрещивающимся силам (см. рис.59).
Такой случай применим в гипоидных передачах, когда передача от вращения ведущей шестерни передается колесу в другую плоскость, т.е. оси вращения звеньев являются перекрещивающиеся.
Рассмотрим подробнее этот случай (см. рис. 59).
,
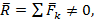 (1)
(1)
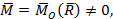 (2)
(2)
Вектор главного момента представим как пару сил в горизонтальной плоскости, как это делали в предыдущих случаях (см. рис 60).

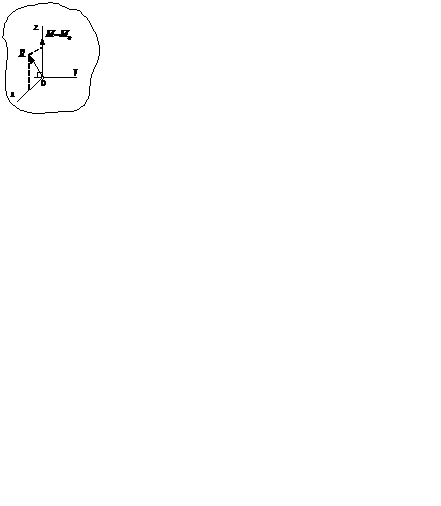
Рис. 59 Рис. 60
Одна из сил пары проходит через точку О, а вторая через точку А на расстоянии h. В точке О проходят линии действий двух сил 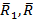 . Они приводятся (см. рис. 61) к равнодействующей
. Они приводятся (см. рис. 61) к равнодействующей  , которая равна
, которая равна
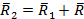 .
.
Окончательно получаем две пересекающиеся силы  и
и 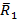 .
.
Сила 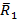 находится в горизонтальной плоскости Оху и её линия действия проходит через точку А.. Сила
находится в горизонтальной плоскости Оху и её линия действия проходит через точку А.. Сила  находится в плоскости Oxz и её линия действия проходит через точку О (см. рис. 62).
находится в плоскости Oxz и её линия действия проходит через точку О (см. рис. 62).


Рис. 61 Рис. 62
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 599; Нарушение авторских прав?; Мы поможем в написании вашей работы!