Центр тяжести 1 страница

Трение

В становлении научных представлений о трении в самом начале большое значение имели два события: открытие Галилеем закона инерции на рубеже 16-17 веков и осознание Румфордом способности механической энергии превращаться в тепло примерно два столетия спустя.

До Галилея примерно на протяжении двух тысяч лет в механике Аристотеля упоминается сопротивлении тел при движении, когда рассматривалось неравномерное движение тела. Изучал трение в средневековье известный механик, художник Леонардо да Винчи. В национальной библиотеке Мадрида были случайно обнаружены две неопубликованные рукописи, получившие название «Мадридский кодекс». В ней Леонардо уже говорил о бессмысленности вечного двигателя: «Стремление создать вечное колесо- источник вечного движения- можно назвать одним из бесполезных заблуждений человека. На протяжении многих столетий все, кто занимался вопросами гидравлики, военными машинами и прочим, тратили много времени и денег на поиски вечного двигателя. Но с ними происходило то же, что и с алхимиками: всегда находилась какая-нибудь мелочь, которая якобы мешала успеху опыта. Моя небольшая работа принесет им пользу: им не придется больше спасаться бегством от королей и правителей, не выполнив своих обещаний». Это было за 200 лет до опытов Амонтона и примерно за три века до публикации работ Кулона по трению.

Леонардо пишет по трению: «сила трения зависит от материала соприкасающихся поверхностей, а также от степени их обработки и не зависит от площади соприкасающихся поверхностей; она прямо пропорциональна весу груза и может быть уменьшена введения «роликов» или смазочных веществ между трущимися поверхностями». Леонардо впервые вводит в инженерный обиход понятие коэффициента трения, отмечая, что всякое трущееся тело оказывает сопротивлении, равное четверти своего веса, при этом он не считает эту величину постоянной, а имеет в виду лишь ее приближенное значение.

Понятие «ролики» означает, что Леонардо имел ввиду ролики в подшипниках качения. По этому поводу их говорил: «не вижу большой разницы между ними (имея ввиду шарики и ролики), исключая ту, что шарики могут вращаться во всех направлениях, а ролики в одном. Но если во время движения шарики или ролики соприкасаются, движение будет более медленным, так как при их касании сила трения будет действовать в противоположном направлении. Но если шарики или ролики находятся на расстоянии друг от друга….это облегчает движение». Здесь впервые сказано о сепараторах, с помощью которых разделяются друг от друга шарики или ролики, применяемые в подшипниках качения.

13.1. Трение скольжения

Трение скольжения возникает в тех случаях, когда скорости точек контакта поверхности тела и поверхности связи различны.

Открытие Галилеем принципа инерции дало возможность разделить между собой силы сопротивления, связанные с инерцией и обусловленные трением. Допустим, рассматриваем прямолинейное и равномерное движение тела: ускорение его равно нулю, это значит, что внешняя сила, приложенная к телу, уравновешивается силой трения.

Амонтон (1699 г.) также в своих работах говорит о том, что сила трения линейно зависит от нагрузки. В современной записи выглядит так:

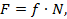
F – сила трения скольжения, N - нормальная сила к плоскости трения,

f - коэффициент трения скольжения. Коэффициент трения зависит от состояния тела: находится или нет тело в движении. Если имеется движение, то f коэффициент трения скольжения (при движении) будет меньше коэффициента сцепления (при покое):

f_cц > f или f_стат > f_движ

отсюда получаем

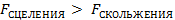или

Таблица коэффициентов трения скольжения

Материалы тел, между которыми возникает трение	Коэффициенты статического трения для поверхностей	Коэффициенты трения движения для поверхностей
сухих	смазанных	смоченных водой	сухих	смазанных	смоченных водой
Сталь по железу	0,15	0,10	-	0,10	0,009	-
Литое железо по чугуну или по бронзе	0,18	0,1	-	0,16	0,01	-
Металл по дереву	0,6-0,5	0,1	-	0,5-0,2	0,08-0,02	0,26-0,22
Дерево по дереву	0,65	0,2	0,7	0,4-0,2	0,16-0,04	0,25
Кожа по металлу	0,6	0,25	0,62	0,25	0,12	0,36
Дерево по камню	До 0,7	0,4	-	0,3	-	-

Коэффициенты трения были найдены экспериментально для ряда комбинаций, между которыми возникает трение. Эти коэффициенты можно найти во многих технических справочниках. Данные, приведенные в таблице, содержат лишь приближенную оценку коэффициентов трения и поэтому пригодны лишь для грубых расчетов. Для определения более точных значений коэффициента трения ставят особые эксперименты.

В 1781 г. Кулон установил основные приближенные законы для сухого трения скольжения при покое. Эти

законы имели подтверждение в случае, когда поверхности не вдавливаются друг в друга и шероховатость не очень велика.

Законы Кулона

1. Силы трения скольжения находятся в общей касательной плоскости соприкасающихся поверхностей тел и направлены в обратную сторону возможному движению (скольжению) тела под действием активных сил. Величина силы трения зависит от активных сил и заключена между нулем и своим максимальным значением, который достигается в момент выхода тела из положения равновесия

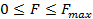
2. Максимальная сила трения скольжен7ия не зависит от площади соприкасающихся трущихся поверхностей. Из этого закона следует, что прикладываемая сила не зависит от того какой поверхностью тело касается другой при скольжении.

3. Максимальная сила трения скольжения пропорциональна нормальному давлению (нормальной реакции)

где f называют коэффициентом трения скольжения; он не зависит от N.

4. Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей, т.е. от величины и характера шероховатости, температуры и других условий. Степень их шероховатостей, она зависит от высоты микронеровностей и делится на 14 классов чистоты. Чем выше эта цифра, тем чище поверхность. Например, изделие после литья имеет 6 класс чистоты, лакированная поверхность мебели – восьмой.

Угол, конус трения и угол естественного откоса

Равнодействующая реактивных сил: нормальной силы и трения равна шероховатой поверхности, 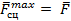– максимальная сила сцепления или сила трения при покое (см. рис. 68).

Рис. 68

Угол 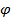является углом сцепления, образован реакцией шероховатой поверхности и нормалью. Тангенс угла сцепления равен коэффициенту сцепления:

Конус с вершиной в точке касания тел, образующая которого составляет угол сцепления с нормалью к поверхностям тел, называется конусом сцепления. Поверхность конуса является геометрическим местом максимальных реакций опорной поверхности. Пусть рассмотрим влияние силы 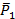на состояние тела. Какая бы большая по величине эта сила не была и действовала на тело, она не сдвинет его с места, т.к. проекция этой силы ось, по которой может быть движение, мала по сравнению с силой сцепления. Отсюда тело нельзя вывести из равновесия, если сила находится внутри конуса.

Рассмотрим другую силу, , действующую по образующей конуса сцепления. Если её проекция на ось, по которой возможно движение, равна проекции реакции 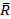на ту же ось, т.е. силе трения сцепления, то состояние тела будет предельным, но в покое: если чуть-чуть увеличить величину силы , то возможно движение тела. Теперь рассмотрим влияние силы на тело. Если её проекция будет больше чем сила трения сцепления, то будет наблюдаться движение.

Теперь рассмотрим наклонную шероховатую плоскость АВ (см. рис. 69), на которой находится тело. Изменяя угол наклона её к горизонту 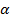, можно достичь такого положения, когда тело начнет свое движение по шероховатой поверхности. Сила тяжести тела на касательную плоскость АВ сравнивается с силой трения.

Если нет движения, то записывается

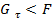, т.к. ,

,

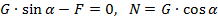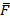сила трения является силой сцепления, величина её равна

,

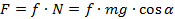где G=mg. g – ускорение свободного падения и равно примерно g 10 м/с². Чем меньше угол тем больше сила трения. Состояние предельного равновесия будет

,

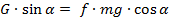т.е. проекция силы тяжести на касательную ось 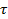равна силе трения. Следовательно, угол 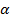,который называется углом естественного откоса, равен углу трения

.

Рис. 69

13.2. Трение качения

Если тело имеет форму катка и под действием приложенных активных сил может катиться по поверхности другого тела, то из-за деформации поверхностей этих тел в месте их соприкосновения могут возникнуть силы реакции, которые препятствуют и скольжению и качению.

Вначале рассмотрим движение катка по горизонтальной плоскости под действием активных сил. Соприкосновение катка с плоскостью происходит не в одной точке, а по некоторой площадке (см. рис. 70).

Рис.70

Когда происходит деформация по площадке BD, то появляется реакция шероховатой поверхности 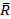, которая имеет проекци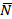и и 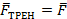, причем результирующая реакция 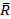находится в точке А, в стороне от центральной вертикальной оси на расстоянии от неё, если накат катка происходит влево. Коэффициент трения качения имеет размер длины. В первом приближении сила трения скольжения как вектор берет начало с нижнего вертикального положения диаметра катка, т.е. с точки В.

Рассмотрим только чистое качение катка по горизонтальной плоскости, когда отсутствует скольжение, т.е. сила трения скольжения равна нулю (см. рис. 71).

Когда деформируется горизонтальная поверхность, которая явно показана на рис.70 и на рис.71, появляется момент трения качения. Момент трения качения представляет собой пару сил 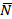и с моментом

,

Рис. 71

где 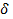является коэффициентом трения качения и имеет размерность длины, расстояния между проекцией силы тяжести на ось, по которой направлен вектор скорости катка, и нормалью. Коэффициент трения качения зависит от материала катка, плоскости и физического состояния их поверхностей. Этот коэффициент в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости.

Таблица коэффициентов трения качения, см⁴

Колесо со стальным бандажом по стальному рельсу	0,05
Деревянный каток по дереву	0,05-0,08
Стальное колесо по дереву	0,05-0,25
Резиновая пневматическая шина по асфальту	0,02
Дерево по стали	0,03-0,04
Подшипник качения (шарикоподшипник)	0,001-0,004
Подшипник качения (роликоподшипник)	0,0025-0,0100
Шарик из закаленной стали по стали	0,0005-0,0010

Момент трения качения направлен в обратную сторону возможному вращению катка (см. направление угловой скорости ).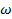

Рассмотрим только чистое качение катка по наклонной плоскости вверх, когда отсутствует скольжение, т.е. сила трения скольжения равна нулю F=0 (см. рис. 72).

Момент трения качения направлен в обратную сторону возможному вращению катка, т.е. в обратную сторону 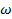, который равен

,

где 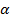угол наклона поверхности к горизонту.

Рис. 72

Возможные случаи при движении катка (см. рис 73)

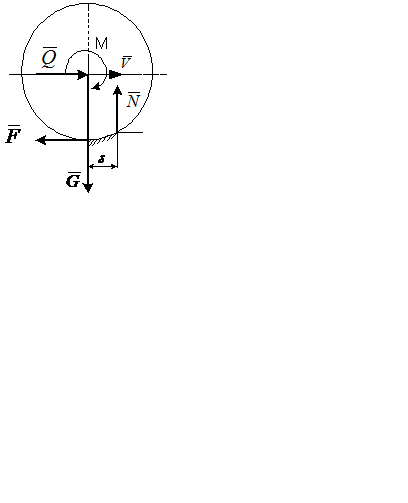
Рис.73

N	Случаи при качении катка	Состояние катка
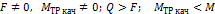
		Скольжение
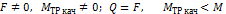
		Качение
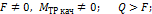
		Качение и скольжение
		Равновесие, покой

13.3. Трение верчения /к.т.м. Лойцянский и Лурье/

В отличие от абсолютно твердых тел, которые могут соприкасаться в одной точке, соприкосновение прижатых друг к другу реальных тел происходит всегда по некоторой площадке. Приведение одного из тел во вращение по другому препятствуют силы трения скольжения, распределенные по площадке соприкосновения и определяющие трение верчения.

Совокупность этих сил может быть приведена к паре, которая уравновешивается парой, приложенной к телу и стремящейся повернуть его вокруг оси, перпендикулярной к площадке соприкосновения.

Определение предельной величины момента пары трения верчения представляет сложную задачу, поскольку этот момент зависит от распределения давлений по площадке соприкосновения, а площадка эта зависит от формы поверхностей и упругих свойств, прижатых друг к другу тел. Предельную величину момента трения верчения М принимают пропорционально прижимающей силе 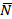и определяют формулой

где 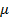- коэффициент трения верчения, имеющий размерность длины. Этот коэффициент зависит от

коэффициента трения скольжения f. Например, при соприкосновении плоского основания круглого цилиндра радиуса а с плоской поверхностью коэффициент трения верчения может быть определен теоретически и оказываться равным

.

В более сложном случае соприкосновения тел, ограниченного поверхностью вращения, с телом,

ограниченным плоской поверхностью, имеем

,

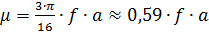где а - радиус образующейся при соприкосновении тел круговой площадки, который зависит от силы прижатия тел друг к другу, от радиуса кривизны поверхности вращения в точке соприкосновения её с плоской поверхностью и от упругих свойств постоянных*.

Еще пример, наматывание нити на шпульку в швейной машинке; наматывание на веретено разной формы нити в ткацком станке, намотка троса на катушку; намотка провода на катушку и т.д.

14.1. Приведение двух параллельных сил

___________________________________________________

*) Галин Л.А. Контактные задачи теории упругости. - M.: Гостехиздат, 1953, с. 204.

Случай 1. Приведение двух параллельных сил, ориентированных в одну сторону

Рассмотрим две силы 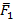и 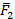, которые параллельны и ориентированы в одну сторону, , 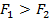(см. рис. 74).

Рис. 74

Если две силы ориентированы в одну сторону и они параллельны, то они приводятся к равнодействующей 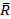, ориентированной в ту же сторону, параллельной и равной алгебраической их сумме. Точка приложения равнодействующей обратно пропорциональна их величинам.

В самом деле, докажем это утверждение. Запишем условие равновесия заданных двух сил относительно точки С, через которую проходит линия действия равнодействующей и точка С расположена на прямой А и В, где проходят линии действий заданных сил 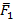и

=0.

Отсюда,

,

Утверждение доказано.

Случай 2. Приведение двух параллельных сил, ориентированных в разные стороны

Рассмотрим две силы 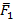и 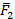, которые параллельны и ориентированы в разные стороны, 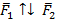, 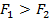(см. рис. 75).

Рис. 75

Если две силы ориентированы в разные стороны и они параллельны, то они приводятся к равнодействующей 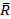, ориентированной в сторону большей по модулю силы, параллельна и равна алгебраической сумме сил 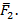Точка приложения равнодействующей обратно пропорциональна их величинам.

Равнодействующая сила 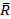в этом случае находится за большой по модулю силой, в данном случае за силой 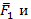линия действия её проходит через точку С, которая находится на прямой расположения точек А и В. Запишем условие равновесия заданных двух сил относительно точки С

=0.

Отсюда,

,

Утверждение доказано.

14.1.2.Приведение системы параллельных сил

Рис. 76

Случай 1. Приведение к равнодействующей

Дана система параллельных сил ориентированных в разные стороны (см. рис. 76). Допустим. даны четыре параллельные силы 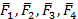. Из них силы 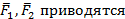к равнодействующей 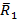, 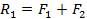. Также приведем к равнодействующей другие две силы

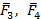, где 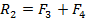. Обе равнодействующие параллельны и ориентированы в одну сторону. Приведем их к результирующей, она равна по величине

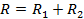
место её приложение обратно пропорционально составляющим 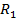и , где они могут быть равны и не равны между собой по модулю (см. случай 1, с. 114).

Случай 2. Приведение к паре сил

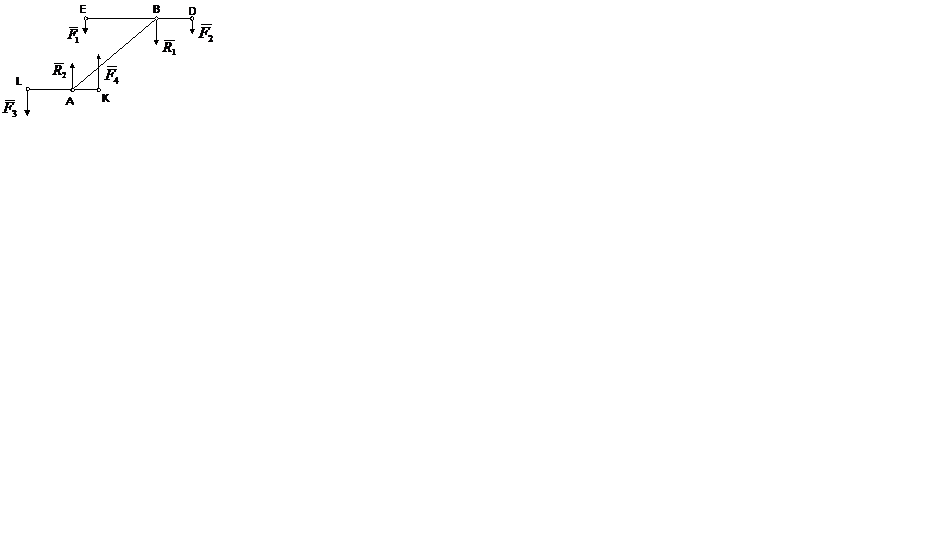
Рис. 77

Дана система параллельных сил ориентированных в разные стороны (см. рис. 77). Допустим. даны четыре параллельные силы 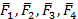. Из них силы 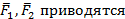к равнодействующей 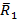, где

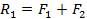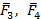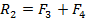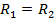. Также приведем к равнодействующей другие две силы , где . Обе равнодействующие параллельны и ориентированы в разные стороны, причем, они равны по модулю и не лежат на одной прямой. Данная система сил

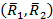приводится к паре сил, момент пары сил равен

.

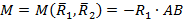Отсюда, данная система параллельных приводится к паре сил.

Случай 3. Приведение к равнодействующей силе

Рис. 78

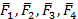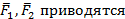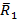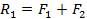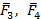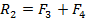Дана система параллельных сил ориентированных в разные стороны (см. рис. 78). Допустим. даны четыре параллельные силы . Из них силы к равнодействующей , . Также приведем к равнодействующей другие две силы , . Обе равнодействующие параллельны и ориентированы в разные стороны, причем, они не равны по модулю 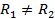и не лежат на одной прямой. Данная система сил 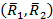приводится к равнодействующей 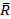(cм. случай 2, с. 115),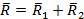

Случай 4. Приведение к уравновешенной системе

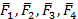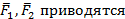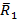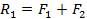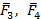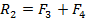Дана система параллельных сил ориентированных в разные стороны (см. рис. 79). Допустим. даны четыре параллельные силы . Из них силы к равнодействующей , . Также приведем к равнодействующей другие две силы , . Обе равнодействующие параллельны и ориентированы в разные стороны, причем, они не равны по модулю 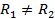и лежат на одной прямой. Данная система сил 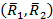приводится к уравновешенной системе сил .

Дата добавления: 2015-06-04