
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Центр тяжести 2 страница
|
|
|
|

Рис. 79
Вывод.
1. Система параллельных сил приводится к равнодействующей 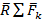 , где k=1, 2, ….,n.
, где k=1, 2, ….,n.
2. Система параллельных сил приводится к паре сил с моментом  .
.
3. Система параллельных сил приводится к системе уравновешенных сил 
14.2 Центр тяжести твердого тела
Рассмотрим случай, когда параллельные силы приводятся к равнодействующей. Считаем, что векторы сил ориентированы в одну сторону, они являются силами тяжестей каждой точки тела. Найдем положение радиус-вектора результирующей силы – силы тяжести тела (см. рис. 80).
Рис. 80
Тело состоит из множества точек, где 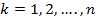 .
.
Положение к-ой точки определяется радиус-вектором 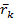 .
.
Каждая точка имеет вес или силу тяжести  . Все силы тяжести точек тела параллельны и направлены строго вертикально вниз. Равнодействующая сил тяжестей составляет силу тяжести тела
. Все силы тяжести точек тела параллельны и направлены строго вертикально вниз. Равнодействующая сил тяжестей составляет силу тяжести тела  , её линия действия проходит через точку С. Положение точки С определяет радиус-вектор
, её линия действия проходит через точку С. Положение точки С определяет радиус-вектор  . На основании теоремы Вариньона о моменте равнодействующей относительно любого центра приравняем момент равнодействующей относительно центра О геометрической сумме моментов составляющих сил относительно этого центра:
. На основании теоремы Вариньона о моменте равнодействующей относительно любого центра приравняем момент равнодействующей относительно центра О геометрической сумме моментов составляющих сил относительно этого центра:
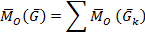
или
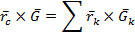
Введем единичный вектор  . Параллельный линиям действий сил. Тогда получим
. Параллельный линиям действий сил. Тогда получим
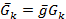 ,
, 
Подставим полученные значения в выражения моментов
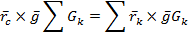
Переместим скалярные множители в векторных произведениях:

Вектор  по модулю не равен нулю, является ускорением свободного падения и
по модулю не равен нулю, является ускорением свободного падения и  . Тогда получаем
. Тогда получаем
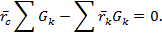
Откуда выразим
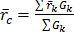 (1)
(1)
Запишем радиус-вектор центра тяжести
 .
.
Получим формулы для вычисления координат центра тяжести тела
 ,
,  ,
,  . (2)
. (2)
У однородного тела плотность одинакова, т.е. тело выполнено из одного материала. Тело может быть объемным, где  , плоским, где F - его площадь, и иметь один размер – длину, где L - его длина.
, плоским, где F - его площадь, и иметь один размер – длину, где L - его длина.
Выразим силу тяжести плотность:
для объемного тела  ; плоского тела
; плоского тела  ; тела, имеющего один размер,
; тела, имеющего один размер, 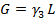 . Тогда формулы для определения координат центра тяжести тела имеют вид: для объемного тела
. Тогда формулы для определения координат центра тяжести тела имеют вид: для объемного тела
 ; (3)
; (3)
для плоского тела
 ,
,  ; (4)
; (4)
для тела, имеющего один размер,
 ,
,  ,
, 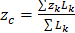 . (5)
. (5)
Координаты центра тяжести тела на плоскости могут быть выражены через статические моменты относительно осей х и у:
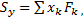
 (6)
(6)
В этом случае формулы (4) примут вид
 ,
,  . (7)
. (7)
Применение (7) используется в сопротивлении материалов.
14.3.Способы определения положения центра
тяжести тел
Положение центра тяжести тела и величина силы тяжести влияют на устойчивость при равновесии. Равновесие тела может быть и не быть. Равновесие может быть устойчивым, а может и неустойчивым. Пример, если карандаш поставить на его торец, то неустойчивое равновесие, а если его положить на горизонтальную плоскость, то устойчивое равновесие. Все зависит от величины потенциальной энергии силы тяжести, чем она меньше, тем устойчивое состояние тела.
Для определения или изменения положения центра тяжести тела существуют метод, который делится на расчетный или теоретический способ и практический или экспериментальный способ.
Экспериментальным способом находят положение центра тяжести или его изменяют, причем для сложных конструкций. Изменение положения центра тяжести конструкции влияет на её устойчивость в рабочем состоянии.
Расчетный способ применим, когда тело сложной конфигурации можно разделить на простые тела, формулы для определения центров тяжестей известны. Если тело имеет пустоты, то они считаются как отрицательные тела и берутся со знаком минус «-».
Например, возьмем в системе вентиляции трубу для вытяжки в сечении условно, т.к. в реальности учитывается только толщина стенки

Рис. 81
Разобьем фигуру на простые тела: полукруг – тело1 радиусом 30 см; прямоугольник с размерами 60 см на 20 см
– тело 2; четверть круга радиусом 20 см – тело 3; прямоугольник с размерами 60 см на 20 см – 4; квадрат 10см на 10см – тело 5.
Для определения центра тяжести фигуры используем формулы (4).
 ,
, 
Распишем координату на ось х

В примере показано разбиение тела на простые тела с использованием способа отрицательных тел, тело 5 является отрицательным.
Прежде чем записывать координаты центра тяжести тела требуется выбрать систему координат. Ниже будут показаны формулы для определения центров тяжестей простых тел. Поэтому полное решение этого примера см. в конце п. 13.4.
14.4. Центры тяжести некоторых линий,
плоских фигур и тел
1. Однородный плоский треугольник
(см. рис. 82)
Центр тяжести такой фигуры находится на пересечения медиан. Если рассматривать тонкие полоски с каждой стороны треугольника, то видно, что центы тяжестей полосок находятся на медианах к сторонам треугольника. Это рассматривалось при рассмотрении распределенной силы, см.12.
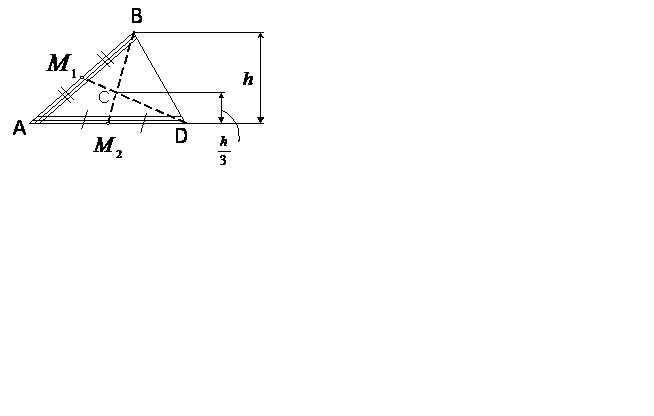
Рис. 82
2. Центр тяжести однородной дуги
Возьмем дугу АВ окружности радиуса R с центральным углом 2 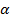 (см. рис. 83). Проведем ось х как ось симметрии. Если тело имеет ось симметрии, то центр тяжести его лежит на этой оси. Используем формулу
(см. рис. 83). Проведем ось х как ось симметрии. Если тело имеет ось симметрии, то центр тяжести его лежит на этой оси. Используем формулу
 .
.
Длина дуги равна  , где
, где  - центральный угол в радианах. Разбиваем дугу на бесконечно малые элементы длиной
- центральный угол в радианах. Разбиваем дугу на бесконечно малые элементы длиной  и вычисляем координату
и вычисляем координату 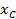 :
:
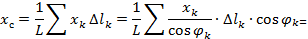
 .
.
Окончательно получаем
 , (8)
, (8)
где 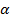 - половина центрального угла, измеряется в радианах. Мы не рассматриваем малые угла, т.е.
- половина центрального угла, измеряется в радианах. Мы не рассматриваем малые угла, т.е. 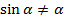 ,
,
поэтому центр тяжести дуги находится внутри сектора АОВ.

Рис. 83
3. Центр тяжести площади сектора круга
Разбиваем сектор круга с центральным углом  , на бесчисленное множество элементарных секторов (см. рис. 84).
, на бесчисленное множество элементарных секторов (см. рис. 84).
Каждый элементарный сектор рассматривается как треугольник высотой R и основанием  , центр тяжести которого находится на расстоянии 2/3
, центр тяжести которого находится на расстоянии 2/3 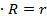 .
.
Отсюда по формуле
 (9)
(9)

Рис.84
Площади и координаты центров тяжести некоторых плоских и объемных фигур приведены в таблице.
| Плоская фигура | Площадь | Координаты центра тяжести | |
| Треугольник | 
|  h h
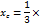
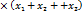 ,
х1, х2, х3 –координаты вершин ОАВ ,
х1, х2, х3 –координаты вершин ОАВ
| |
| Круговой сектор | 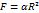
| 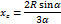
| |
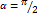 полукруг полукруг
| 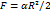
| 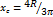
| |

| 
| 
| |
| Дуга | Длина дуги
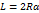
| 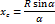
| |
| Трапеция | 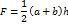
| 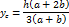
| |
| Круговой сегмент | 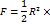
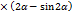
| 
| |
| Объемная фигура | Объем | Координаты центра тяжести | |
| Четырехгранная пирамида |  S- площадь основания
S- площадь основания
| 
| |
| Многогранная пирамида |  S- площадь основания
S- площадь основания
| 
| |
| Конус | 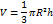 S- площадь основания
S- площадь основания
| 
| |
| Усеченный конус |  S1- площадь большого
основания
S2- площадь
малого
основания
S1- площадь большого
основания
S2- площадь
малого
основания
| 
| |
| Шар | 
| ||
| Полушар | 
|  R R
| |
| Шаровой сегмент | 
| 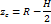
| |
| Шаровой сектор | 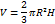
| 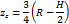
|
Данные в таблице собраны для информации при решении задач на определения центра тяжести тела, используя любой задачник по теоретической механике.
Пример. Определение центра тяжести плоской фигуры.
Найти координаты центра тяжести заданной фигуры, размеры указаны в сантиметрах.
Решение. Координаты центра тяжести плоской фигуры определяем по формулам:
 ,
, 
Разобьем фигуру на простые тела, для которых легко определить площади и координаты центров тяжестей
 где k=1,2,..,5: полукруг – тело1 радиусом 30 см; прямоугольник с размерами 60 см на 20 см
где k=1,2,..,5: полукруг – тело1 радиусом 30 см; прямоугольник с размерами 60 см на 20 см
– тело 2; четверть круга радиусом 20 см – тело 3; прямоугольник с размерами 60 см на 20 см – 4; квадрат 10см на 10см – тело 5.
Распишем координаты цента тяжести фигуры на оси х, у:
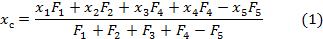
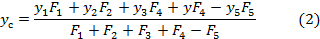
Прежде чем записывать координаты центра тяжести тела требуется показать координатные оси х, у.
Вычисляем координаты центров тяжестей пяти составляющих тел фигуры, ответы даны в см:
 ,
,







Все расчетные данные запишем в таблицу
| N | Площадь, см2 | Координата хк | Координата ук |
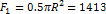
| 72.74 | ||

| |||
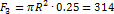
| 8.49 | -8.49 | |
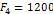
| -30 | -10 | |
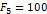
| -45 | -10 |
По формулам (1), (2) вычисляем координаты центра тяжести заданной фигуры:
 31.07 см.
31.07 см.
Покажем точку С на рисунке с данными координатами.
Вопрос:
Как изменится центр тяжести, если в данной задаче рассмотрим одинаковую толщину каждой детали?
14. Контрольные вопросы
15. Примеры задач на равновесие объекта
15.1 Равновесие объекта под действием сходящихся сил
15.2 Равновесие объекта под действием произвольной
плоской системы сил
15.3 Равновесие объекта под действием произвольной
пространственной системы сил
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 553; Нарушение авторских прав?; Мы поможем в написании вашей работы!