Аксиомы статики

Силы и их классификация

Объект. Силы и их классификация

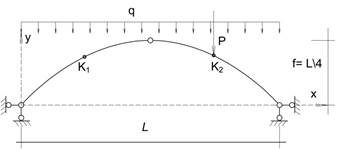
Расчёт трёхшарнирной арочной фермы

Расчёт трёхшарнирной арки

Схема арки Исходные данные

Размеры, м	Расчётная нагрузка
L	f	q, кН/м	Р, кН

y = 4f/ L² - парабола

Требуется:

1. Вручную определить опорные реакции и внутренние усилия в арке: изгиб, моменты, поперечные и продольные силы в т. К1 и К2, расположенных в четвертях пролёта.

2. Расчётом на ПК определить опорные реакции и внутренние усилия: изгиб, моменты, поперечные и продольные силы во всех точках.

Исполнитель: студент ___________________________________________ курса _______ группы

Срок выполнения _______________________ Преподаватель: Мещеряков Ю.М.

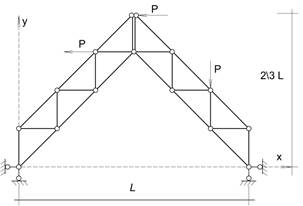
Задание №1 по статике сооружений Вариант 12

Схема фермы Исходные данные

Размеры, L,м	Расчётная нагрузка
L	Р, кН

Требуется:

1. Вручную определить опорные реакции и продольные силы в стержнях арочной фермы в сечениях 1-1 и 2-2.

2. Расчётом на ПК определить опорные реакции и продольные силы во всех стержнях арочной фермы.

Исполнитель: студент ___________________________________________ курса _______ группы

Срок выполнения _______________________ Преподаватель: Мещеряков Ю.М.

1.1 Объект

В качестве объекта в механике рассматриваются точка, твердое тело и механическая система точек и тел.

· точка это тело, у которого нет размеров, точка имеет массу. Точка находится в пространстве или на плоскости. Траектория её является кривая или прямая. Надо сказать, что в статике рассматривается равновесие объекта в покое, т.е. при остановленном времени

После равновесия точки перейдем к системе материальных точек, связанных между собой, которая представляет либо:

I. Тело, которое обладает размерами, может быть объемным, плоским и объектом, который имеет только один размер. Тело может находиться в одном из пяти движений: поступательном, вращательном, плоском, сферическом, общем случае. Равновесие тела рассматриваем также в покое.

В теоретической механике согласно аксиоме отвердевания рассматриваются тела, как абсолютно твердые, они не деформируются (не изменяют свою форму) и расстояние между любыми точками тела всегда остается постоянным (см. рис.1).

II. Кроме точки и твердого тела рассматривается механическая система. Слово «механическая» означает, что система находится в механическом движении, система состоит из нескольких тел, связанных между собой, например, кривошипно-шатунный механизм; редуктор и т.д. Движение объекта по отношению к неподвижной системе координат или по отношению к наблюдателю называется механическим движением. Изменение положения объекта в пространстве и во времени является механическим движением.

В теоретической механике рассматривается неизменяемые механические системы, т.е. идеальные системы, когда существующая связь между телами остается идеальной всегда, например, механизм подъема состоит из лебедки и груза, которые связаны между собой тросом, трос это связь (нить), считается идеальной, он растягивается и не сжимается (см. рис.2). Это положение лежит в основе аксиомы 3, которая будет рассмотрена ниже (см. п.2, с. 22).

После изучения разделов «Статика» и «Кинематика» параллельно с изучением раздела «Динамика» Вы изучаете курс «Сопротивление материалов», где будете рассматривать различные деформации тел, а пока рассматриваем абсолютно твердые тела и неизменяемые системы.

Рис. 1 Рис. 2

Вопросы для самоконтроля

1. Какие разделы есть в теоретической механике?
2. Что изучается в разделе «Статика»?
3. На какие группы делится объект?
4. Чем отличается абсолютно твердое тела от нетвердого?
5. Каким признаком обладают неизменяемые системы?
6. Что называется механическим движением?
7. Чем отличается точка от тела?

Задание 1.

Разделите предложенные объекты (точка, тело, система тел) на три группы. В качестве объекта может быть: мяч, табуретка, пуля, кнопка, куб, каток, мотор, механизм подъема, кривошипно-шатунный механизм, редуктор, доска, ластик, кульман.

Задание 2. Приведите примеры, где рассматриваются твердое тело и нетвердое; изменяемая система и неизменяемая.

Задание 3. Приведите примеры, которые рассматривают механическое движение и немеханическое.

Задание 4. Приведите примеры, в которых рассматривается состояние объекта в покое и не в покое.

Состояние объекта зависит от того действует на него сила или система сил. Поэтому рассмотрим понятие силы.

Сила есть мера механического воздействия одного объекта на другое.

Приведены примеры действия силы через объект на другой объект (Справочник по физике и технике).

	Сила удара футболиста по мячу	10^4 Н
	Сила тяготения между Землей и Солнцем	10^23 Н
	Сила тяготения между Землей и Луной	10^21 Н
	Сила удара боксера	10^3 Н
	Сила тяги двигателей ракеты, выводившей на орбиту «Союз»	10^5 Н
	Сила притяжения электрона и протона	10^-8 Н

С другой стороны можно привести примеры действия силы на объект, например, скорость - одну из кинематических характеристик (Аргументы и факты № 49, 2005 год).

№	Вид спорта	Скорость полета	Кто и когда установил рекорд
	Футбол	126 км/час или 35 м/с	Рикардо Лима (Бразилия) 2001год
	Волейбол	Около 130 км/час Или 36 м/с	(официальные данные не зарегистрированы)
	Хоккей	169,6 км/час Или 47 м/с	Шон Хейнс (США), матч «Всех звезд НХЛ», 1999 год
	Теннис	244,6 км/час Или 67,9 м/с	Энри Роддик (США), ¼ финала Кубка Дэвиса, 2004 год
	Бадминтон	Около 260 км/час Или 72,2 м/с	(официальные данные не зарегистрированы)

В теоретической механике сила рассматривается как вектор скользящий. Сила как вектор имеет направление, точку приложения, модуль или величину и может перемещаться вдоль линии действия силы (см. рис. 3). Сила измеряется в системе СИ в ньютонах, в технической системе в кГм. В результате действия силы возникает механическое взаимодействие материальных тел и с течением времени происходит изменение взаимного положения этих тел в пространстве. Например, изменение взаимного положения ремня в ременной передаче; поворот шестеренок в часовом механизме; изменение положения кривошипно-шатунного механизма или остановка механизмов и т.д.

На объект действует одна или одновременно система нескольких сил. Для этого рассмотрим классификацию сил.

КЛАССИФИКАЦИЯ СИЛ

I. По расположению сил

(по направлению линий действий сил)

1. Сходящиеся силы.

Дадим определение понятия сходящихся сил.

Если линии действия сил пересекаются в одной точке, то силы называются сходящимися.

Например, узлы в фермах башен, плоские фермы при постройке крыш домов жилых и производственных помещений, различных решетках и т.д. (см. рис.3). Силы могут быть расположены в пространстве и на плоскости.

Сходящиеся силы, действующие на объект, сколько бы их ни было, приводятся к равнодействующей силе. Равнодействующая сила не изменяет состояние объекта, в каком бы состояние объект не находился под действием системы сил. Покажем графический способ определения равнодействующей по правилу сложения векторов.

Рис.3

Рис.4

Рис. 5

На рис.5 показаны две сходящиеся силы, которые приводятся к равнодействующей 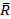, которая эквивалентна системе двух сил, объект не изменяет своего состояния 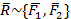и и .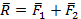

Рис.6

На рис.6 показаны четыре сходящиеся силы, которые приводятся к равнодействующей 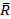. Графическое сложение векторов можно использовать только при соблюдении правильного направления их и верного отложения величин векторов. В такой последовательности: к концу первого вектора приложим начало второго вектора, к концу второго вектора приложим начало третьего вектора и т.д. Если соединим начало первого и конец последнего вектора, то получим нахождение равнодействующей системы сходящихся сил. Равнодействующая сила не изменяет состояния объекта, её можно записать

, .

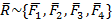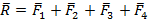Можно приводить к равнодействующей систему из сколько угодно сходящихся сил

, .

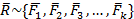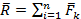Равнодействующая сила по модулю и направлению находится или графическим сложением векторов, как это было сделано для четырех сходящихся сил, или расчетным путем, т.е. аналитически.

Вопросы для самоконтроля

1. Дайте определение силы.

2. Назовите размерность силы.

3. Дайте определение сходящихся сил.

4. К чему приводится система сходящихся сил, начиная с двух?

5. Как графически найти величину и направление равнодействующей силы?

6. Запишите выражение для равнодействующей силы.

Задание 1. Разделите предложенные силы на две группы: удар по мячу рукой или ногой, передвижение шахматной фигуры по доске, академическая гребля в четверках, бобслей-однерки, бобслей-двойки, синхронное плавание, парный велосипед, одиночное фигурное катание, запись карандашом, корректировка текста с помощью штриха.

Задание 2.

1. Правильно ли, что на результативность в боксе действует система ударов?

2. При забеге на дистанцию на конькобежца действует одна сила?

3. Под действием одной или нескольких сил летит мяч в корзину при игре в баскетбол?

4. Назовите силы, действующие на человека при ходьбе.

5. Какими признаками обладает сила?

6. При игре на пианино действует одна или несколько сил?

2. Параллельные силы.

Если линии действия сил параллельны друг к другу и не обязательно ориентированные в одну сторону, то их называют параллельными.

Они могут быть расположены в пространстве и в плоскости. Примером могут быть силы тяжести объектов на планете «Земля». На самом деле линии всех сил тяжестей направлены к центру Земли. Объекты в сравнении с Землей очень и очень малы, поэтому линии сил тяжести считаются параллельными. Известна погрешность отклонения от параллельности этих сил тяжестей в градусах, равна 2 минуты или одна тридцатая градуса.

Рис. 5

Показаны параллельные силы, ориентированные в разные стороны и (см. рис.5 а) и в одну сторону (см.рис.5 б). Параллельные силы также как сходящиеся силы приводятся к равнодействующей силе (см. второй признак классификации сил: распределенные силы и сосредоточенную силу).

3. Произвольно расположенные силы.

Называются силы, у которых линии действия их расположены произвольно друг другу в пространстве и в плоскости (см. рис.6).

Рис. 6

II. По месту действия силы

1. Сосредоточенная сила.

Сила, действующая на тело в какой-нибудь точке, называется сосредоточенной силой.

Например, удар молота о наковальню. На рис.7 показана действующая сила в точке А данного тела-бруса, является сосредоточенной силой.

Рис. 7

Кроме сил, действующих в одной точке, есть силы, которые действуют на определенную длину и на конкретную площадь объекта. Такие силы называют распределенными. Рассмотрим их действие на конкретной длине объекта.

2. Распределенные силы.

Силы параллельные и ориентированные в одну сторону с интенсивностью q с размерностью 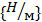, называются распределенными.

Они заменяется сосредоточенной силой 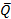, которая равна площади фигуры и находится в её центре (см. рисунки 8, 9, 10).

В качестве примера возьмем любой строительный материал: доски, кирпичи, цемент и т.д., которые лежат на полу, они могут быть расположены произвольно и давить на пол с интенсивностью q.

Рассмотрим приведение распределенной нагрузке по линейному и нелинейному законам. На рис.8а на балку по длине l действует распределенная сила с интенсивностью q, её размерность равна [H/м]. В поперечном сечении показан прямоугольник, это значит, что интенсивность q постоянна по всей длине l. Центр прямоугольника как фигуры находится на пересечении диагоналей, в которой находится сосредоточенная сила, эквивалентная распределенной нагрузке и она равна площади этой фигуры (см. формулу (1)).

а б

в г

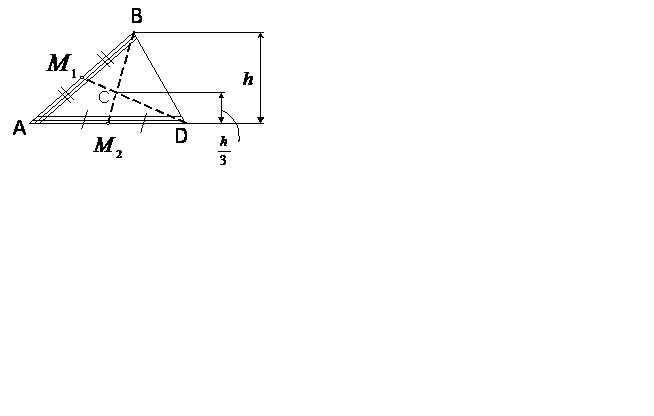
Рис. 8

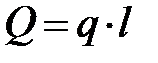(1)

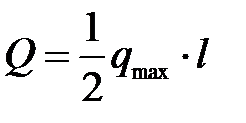(3)

На рис.8б тоже показана распределенная нагрузка, которая изменяется по линейному закону. На рис рис.8в тоже однородный, но прямоугольный треугольник, найдем центр тяжести этого треугольника. Для этого рассмотрим рис.8г, где показан однородный треугольник, мысленно отрежем тонкую полоску со стороны АВ, центр тяжести её находится в середине, если после первой полоски также отрезать вторую полоску, то получаем центр тяжести в середине, значит середина каждой полоски, которая параллельна стороне находится на медиане 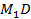стороны АВ. Рассуждая также для стороны AD данного треугольника ABD, получим, что центр тяжести однородного треугольника находится на пересечении медиан 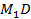и 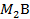. Положение центра тяжести или точки С, показана на рис. 8в и расположена на 1/3 высоты от основания. Положение центра тяжести для распределенной нагрузки, которая изменяется по линейному закону для рис.8б и рис.8в, найдено аналогично и находится на пересечении медиан. Величина сосредоточенной силы находится по формуле (2) см. рис.8б и по формуле (3) см. рис.8в.

Задание.

Самостоятельно найдите положение центра тяжести и величину силы 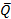на рис. 9а, рис. 9б.

а

б

Рис. 9

III. По известности

1. Активная сила. Под активной силой подразумевается известная по величине и направлению сила, которая действует на объект. Например, сила тяжести, сила ветра, сила удара и т.д.

2. Реактивная сила. Реактивная сила неизвестная по величине и направлению, зависит от крепления одного объекта к другому и от действия активных сил. Рассматривается реактивная сила после прохождения различных опор и аксиомы 6. Реактивная статическая сила находятся из расчета на равновесие объекта. Направление реактивной силы зависит от вида опоры, которая ограничивает движение тела в месте её крепления.

IV. По характеру изменения силы

1. Постоянные силы. Такие силы свою величину не изменяют с течением времени и остаются всегда постоянными по модулю, например сила тяжести объекта.

2. Переменные силы. В общем случае силы бывают переменными, но при прохождении раздела «Статика» мы будем всегда рассматривать постоянные по модулю и направлению силы. К переменным силам относятся такие силы, которые с течением времени изменяют свою величину и направление, например, сила ветра и т.д.

V. Разновидность систем сил

по их приведению

1. Равнодействующая сила.

Если система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системе сил, например, действие сходящихся сил заменяются равнодействующей. При этом состояние объекта не изменяется.

2 Уравновешенная система сил.

Пусть имеем две силы. Они лежат на одной прямой, противоположно ориентированы и равны по модулю. Такая система сил эквивалентна нулю и не влияет на состояние объекта или они уравновешены. Например, в игре натягивание каната две команды тянут канат к себе. Если силы у команд равные, то они будут уравновешены.

Например,

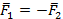
Рис. 10

В общем случае, когда имеем много сил, они эквивалентны нулю, то система сил уравновешена и свободное тело находится в покое

,

где количество сил изменяется от одного до n (k=1,2,….,n).

3. Эквивалентные системы сил.

Рассмотрим две независимые друг от друга системы сил, действующие на одно и то же тело по очереди. Они производят одинаковое механическое воздействие, т.е. состояние тела не изменяется. Такие две системы называют эквивалентными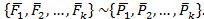

VI. Системы сил по отношению к объекту

1. Внешние силы. Силы, действуя на частицы тела со стороны других тел, называют внешними силами.

На рис. 11а показаны внешние силы, они извне действуют на объект, силы 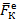, где k обозначает количество сил k=1,2,…n, индекс е означает, что сила внешняя.

Рис. 11

2. Внутренние силы. Эти силы действуют на частицы данного тела со стороны других частиц этого тела, их называют внутренними силами 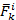, где k=1,2,…,n, индекс i означает, что сила является внутренней. Например, движение частиц воды в трубе и их взаимодействие между собой. На рис.11б показаны две внутренние силы, действующие друг на друга из заданных точек А и В, а могут быть внутренних сил больше двух.

После рассмотрения всех разновидностей сил познакомимся с аксиомами, которые являются правилами для изучения статики, как раздела дисциплины «Теоретическая механика».

Контрольные вопросы

1. Перечислите виды объектов.

2. Чем они отличаются друг от друга?

3. Что называется силой?

4. Какими признаками обладает сила?

Перечислите их.

5. Дайте определение сходящихся сил.

6. К какой силе приводятся сходящиеся силы?

7. Кроме сходящихся сил ещё какие силы Вы

знаете? Перечислите их. Дайте им

характеристики.

8. Чем отличаются сосредоточенная сила и

распределенная нагрузка?

9. К чему приводится распределенная нагрузка,

чему она равна и где расположена?

10. Дайте отличия активной силы от реактивной

силы.

11. Всегда ли силы постоянны? Приведите

примеры.

12. Что называется равнодействующей силой?

Приведите примеры

13. Каким свойством обладает уравновешенная

система сил?

14. Каким свойством обладает эквивалентная

система сил?

15. Чем отличаются внешние силы и

внутренние силы? Приведите примеры.

АКСИОМА 1. Первый закон механики, закон инерции, или закон Галилео Галилея. Закон читается так;

Всякое тело находится в состоянии покоя или равномерного и прямолинейного движении, если на него не действуют никакие силы.

Эта аксиома применима к объектам, которые движутся по отношению к неподвижной системе или по отношению к неподвижному наблюдателю. На самом деле неподвижных систем нет: Земля, как планета, вращается вокруг своей оси и её нельзя считать неподвижной. Планета вращается вокруг своей оси, совершая полный оборот за сутки; ось вместе с Землей движется вокруг Солнца. Солнечная система со своими планетами движется во Вселенной. По этой аксиоме векторная сумма всех сил, действующая на тело, равна нулю в двух случаях: если рассматривать движение тела, то характер движения является равномерным, а траектория – прямой и если рассматривать состояние тела в покое. Например, движение поезда по прямолинейной траектории с постоянной скоростью. Это возможно при условии, что сила тяги и сила трения скольжения уравновешиваются между собой. Второе состояние поезда – это его покой.

АКСИОМА 2. Второй закон механики или основной закон механики.

Если на объект действует сила, то объект получает ускорение пропорциональное силе, вектор ускорения совпадает с направлением вектора силы.

Это основной закон механики, вы его знаете со школы, изучая курс физики в разделе «Механика».

В статике мы будем рассматривать состояние объекта в покое, следовательно, скорость и ускорение его равны нулю. Отсюда сделать можно вывод: любые объекты находятся под действием сил, поскольку мы рассматриваем состояние покой, то векторная сумма сил, действующая на объект, равна нулю. Но в динамике второй закон механики лежит в основе составления дифференциальных уравнений движения объекта.

Надо сказать, что этот закон применим только к объектам, имеющим большие размеры и которые движутся с небольшими скоростями. Например, движение тел со скоростью света мы не рассматриваем. Движение маленьких тел, например, чаинок в стакане при равномерном вращении его не подчиняются этому закону: согласно закону механики они должны убегать от центра под действием центробежной силы, а они движутся к центру.

АКСИОМА 3. Третий закон механики или закон действия и противодействия.

Всякому действию есть равное по величине и противоположно по направлению противодействие.

Как этот закон можно применить к телу? Согласно этому закону расстояние между любыми точками тела является постоянным, это может быть тогда, когда мы рассматриваем абсолютно твердое тело. Допустим, рассмотрим действие силы с одной точки тела на другую и наоборот. Увидим две внутренние силы, которые являются уравновешенными и эквивалентными нулю. Значит, при действии всех внутренних сил точек тела друг на друга имеем: главный вектор всех внутренних сил равный нулю:

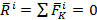или

Рис. 13

Если рассматриваем систему твердых тел, связанных между собой определенными связями, т.е. механическую систему, то в этом случае она должна быть неизменяемой по этой же аксиоме.

Например, рассмотрим ременную передачу. Она состоит из шкивов и ремня. Шкивами являются твердые тела, а ремень - гибкая связь, причем, идеальная, у которой расстояние постоянное между любыми её точками.

АКСИОМА 4. Аксиома параллелограмма.

Аксиома параллелограмма позволяет две сходящиеся силы приводить к равнодействующей (см. рис.14, а).

Две силы, линии действия которых пересекаются, приводятся к равнодействующей.

Рис. 14

Модуль равнодействующей силы равен:

.

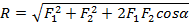К такой равнодействующей силе приводятся сходящиеся силы, сложенные по правилу треугольника (см. рис.14, б).

Правило удобно применять при сложении нескольких сил, получается силовой многоугольник, как это было видно при сложении четырех сходящихся сил (см. п.1,2, с.8).

Правило параллелограмма позволяет раскладывать силу на её проекции в координатных и естественных осях и выполнять обратное действие–сложение проекций.

АКСИОМА 5. Аксиома присоединения.

Или аксиома присоединения уравновешенной системы сил. Действие системы уравновешенных сил не изменяет состояние тела.

Допустим, объект под действием заданных сил находится в определенном состоянии. После этого приложили к этому объекту другую систему сил, эквивалентную нулю. Говоря языком первоклассника: если к числу прибавить ноль или отнять его, то от этого результат не изменится. Значит: состояние объекта не нарушится, если на него действует уравновешенная система сил (см. рис.15).

Рис. 15

АКСИОМА 6. Аксиома освобождаемости от связей. Всякое несвободное тело можно рассматривать как свободное, если убрать связи и заменить их реакциями связей.

В природе нет свободных тел, они все каким-то образом ограничены в движении и связаны с другими объектами. Это зависит от вида крепления тела к другому. Если есть ограничение в движении, то существует связь. А если есть связь, то есть реакции связей, т.е. реактивные силы, они зависят от вида опоры. Всего таких опор двенадцать. Мы их рассмотрим после аксиомы 7 (см.п.3).

АКСИОМА 7. Аксиома отвердевания.

Свойство тела не изменится при его отвердевании.

Эта аксиома позволяет рассматривать все объекты абсолютно твердыми, следовательно, любая реальная задача решается приближенно, потому что реальные тела имеют свойство деформироваться.

Контрольные вопросы

1. Сколько аксиом Вы знаете?

2. Объясните суть первой аксиомы.

3. Объясните суть второй аксиомы.

4. Объясните суть третьей аксиомы.

5. О чем говорится в аксиоме параллелограмма?

6. О чем говорит аксиома присоединения уравновешенной системы сил?

7. Объясните аксиому отвердевания?

8. Изменится ли состояние тела от переноса силы вдоль её линии действия?

Дата добавления: 2015-06-04