
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Действия с силами
|
|
|
|
4.1 Проекции силы на оси
Сила, действующая на объект, по правилу параллелограмма может раскладываться на проекции и наоборот через проекции силы можно найти величину и направление силы.
Для определения проекции силы на координатные оси нужно выполнить действия: опустить перпендикуляры на оси с начала и конца вектора, как это показано на рис. 35, таким образом, находим «след» вектора на оси, на проекциях показано направление проекции. Затем мысленно эти проекции нужно перенести в начала вектора силы, тем самым вектор силы по правилу параллелограмма раскладываем на проекции.
На рис. 35 показана сила в плоскости 0ху, направление силы через угол 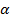 . На рис. 35 есть формулы для вычисления проекций силы, модуль силы и направление силы через направляющие косинусы.
. На рис. 35 есть формулы для вычисления проекций силы, модуль силы и направление силы через направляющие косинусы.
Рис. 35
Это можно объяснить. Рассмотрим прямоугольный треугольник АВС. Сторона АВ есть гипотенуза и результирующая вектора силы 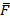 . Катет треугольника: АС есть проекция силы на ось х, т.е.
. Катет треугольника: АС есть проекция силы на ось х, т.е.  , другой катет ВС есть проекция силы на ось у, т.е.
, другой катет ВС есть проекция силы на ось у, т.е.  . Для того, чтобы записать проекцию силы на ось надо смотреть на направление её, если направление вектора совпадает с направлением оси, то пишется знак «+» и наоборот. В данном случае обе проекции записываются со знаком «+». Второе, как использовать тригонометрическую функцию:
. Для того, чтобы записать проекцию силы на ось надо смотреть на направление её, если направление вектора совпадает с направлением оси, то пишется знак «+» и наоборот. В данном случае обе проекции записываются со знаком «+». Второе, как использовать тригонометрическую функцию: 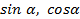 ? Нужно видеть расположение заданного угла: между вектором силы и осью. На рис. 35 угол
? Нужно видеть расположение заданного угла: между вектором силы и осью. На рис. 35 угол 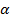 находится между вектором силы и осью х, значит этот угол ПРИ лежит к оси х, следовательно, нужно писать
находится между вектором силы и осью х, значит этот угол ПРИ лежит к оси х, следовательно, нужно писать  Если угол находится против оси, в данном случае ПРО тив оси у, то нужно записывать
Если угол находится против оси, в данном случае ПРО тив оси у, то нужно записывать  . При этом координатные оси мысленно перенести в начало вектора силы. Тогда проекции силы на оси записываются, как показано на рис. 35. Величина силы находится по теореме Пифагора. Направление силы как вектора находится по направляющим косинусам.
. При этом координатные оси мысленно перенести в начало вектора силы. Тогда проекции силы на оси записываются, как показано на рис. 35. Величина силы находится по теореме Пифагора. Направление силы как вектора находится по направляющим косинусам.
Задано шесть сил, из них четыре силы расположены в плоскости в разных четвертях, а последние две силы являются частными случаями направления сил, они параллельны осям х и у соответственно. Рассмотрим (см. рис.37) вычисление алгебраической суммы проекций на координатные оси х и у.
Рис. 36
Из сказанного можно сделать вывод:
1. Проекция силы положительна, если направление её cориентировано с осью.
2. Если линия действия силы параллельна оси, то на эту ось она проектируется в полную величину.
3. Если проекция силы является точкой, то проекции нет, т.к. точка это тело размерами которого пренебрегаем.
4. В каких случаях используется синус угла и косинус угла при записи проекции?
Ответ: если угол находится против оси, от записывать синус угла; если угол прилежит к оси, то записывать косинус угла. При этом координатные оси мысленно параллельно переносятся в начало вектора силы.
Задание.
1. Самостоятельно придумать ситуацию расположение трех сил в пространстве.
2. Записать результирующую силу через её проекции
3. Найти модуль и направление результирующей силы.
4.2 Момент силы относительно точки
Рассмотрим момент силы относительно точки. На рис. 37 показана сила  в пространстве, имеющее начало в точке А на расстоянии
в пространстве, имеющее начало в точке А на расстоянии  радиуса-вектора. Нужно найти момент силы относительно точки 0, начала координатной системы. Для этого проводим плоскость через радиус вектор и вектор силы, см на рис 37 заштрихованную плоскость. К этой плоскости из точки О, как точки относительно которой рассматривается момент силы относительно точки, проводим перпендикуляр, по которому будет направлен вектор момента силы относительно точки. Направление вектора момента находим по правилу буравчика (см. рис. 38).
радиуса-вектора. Нужно найти момент силы относительно точки 0, начала координатной системы. Для этого проводим плоскость через радиус вектор и вектор силы, см на рис 37 заштрихованную плоскость. К этой плоскости из точки О, как точки относительно которой рассматривается момент силы относительно точки, проводим перпендикуляр, по которому будет направлен вектор момента силы относительно точки. Направление вектора момента находим по правилу буравчика (см. рис. 38).
Рис.37
На рис. 38 показан буравчик с правой резьбой (винт, или болт, или шпилька), который вращается против часовой стрелки при завинчивании. Вращаясь, буравчик поднимается вверх и если смотреть сверху на конец вектора-момента, то видно, что буравчик вращается против часовой стрелки.
Перейдем к рис. 37. Вращение вектора силы вокруг перпендикуляра, опущенного из точки 0 на плоскость, проходящую через радиус-вектор и вектор силы, имеет направление против часовой
стрелки. А это значит, что вектор момента
Рис. 38 силы направлен по перпендикуляру вверх
из точки О. Теперь найдем модуль силы относительно центра. Для этого посмотрим фрагмент заштрихованного треугольника (см. рис. 37, и рис. 39). В этом треугольнике найдем кратчайшее расстояние от точки О до линии действия силы (рис 39). Кратчайшим расстоянием является перпендикуляр опущенный из точки О до линии действия силы и называется плечом h. Начала вектора силы переносим в точку В и получаем рычаг, который поворачивается вокруг точки О против часовой стрелки для данного рисунка.
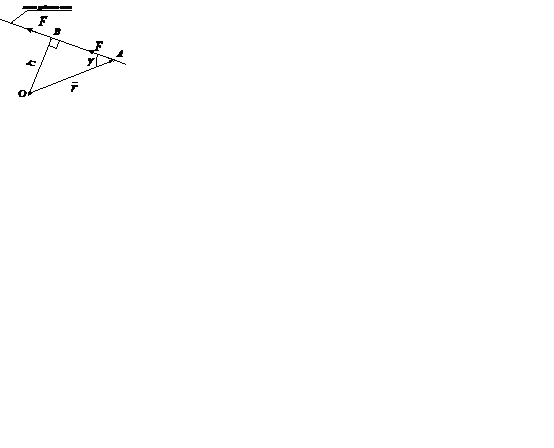 Вычислим векторный момент силы относительно точки (см. рис. 37), если известны координаты точки приложения силы в точке A(x.y.z).
Вычислим векторный момент силы относительно точки (см. рис. 37), если известны координаты точки приложения силы в точке A(x.y.z).
Рис.39
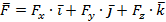 :
:
 (1)
(1)
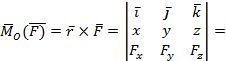
(2)


 (3)
(3)
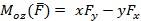 ,
,
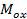 ,
,  ,
,  - проекции векторного момента на соответствующие координатные оси.
- проекции векторного момента на соответствующие координатные оси.
Модуль векторного момента силы относительно точки равен
 (4)
(4)
Величина момента силы относительно точки равна
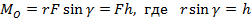 (5)
(5)
 (6)
(6)
Сила может быть расположена так, что вращение её происходит по часовой стрелке и наоборот против часовой стрелки. Поэтому механики договорились, что в статике момент имеет знак «+», если вращение происходит против часовой стрелки и наоборот, если вращение происходит по часовой стрелки, то записывается знак «-».
Задание.
Найдите алгебраическую сумму моментов сил, которые показаны на рис. 39. Если заданы силы 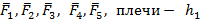 ,
, 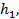
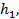
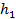 .
.
 Из рис. 40 видно, линия действия пятой силы проходит через точку О, поэтому момент этой силы относительно точки О равен нулю, т.к. отсутствует плечо
Из рис. 40 видно, линия действия пятой силы проходит через точку О, поэтому момент этой силы относительно точки О равен нулю, т.к. отсутствует плечо
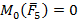
Рис. 40
поскольку h5=0. Запишем алгебраическую сумму моментов остальных сил относительно точки О, используя правило знаков моментов.
Если Вы затрудняетесь, то смотрите ответ:

4.3 Теорема Вариньона
для силы в плоскости
Момент силы относительно точки равен алгебраической сумме моментов проекций этой силы на координатные оси относительно той же точки.
На рис. 41 показано использование теоремы Вариньона для определения момента силы относительно точки А.
Рис. 41
Это правило дает возможность быстрее находить момент силы относительно любой точки через проекции заданной силы, в том случае, если линия действия силы не перпендикулярна оси и не параллельна ей.
По аналогии можно найти момент силы относительно центра в пространстве по формуле:
 ,
,
где  - векторы моментов проекций на плоскость силы относительно координатных осей.
- векторы моментов проекций на плоскость силы относительно координатных осей.
Для этого нужно знать момент силы относительно оси.
Задание.
1. Начертите прямоугольник со сторонами 6 см и 8 см. так, чтобы большая сторона лежала на горизонтали. К правому верхнему углу или вершине прямоугольника приложена сила величиной 100 Н. Угол между линией действия силы и вертикалью составляет 300.
Найдите момент силы относительно остальных трех вершин прямоугольника. Начните решение по ходу часовой стрелки, т.е. первая вершина или точка будет являться правой нижней вершиной прямоугольника.
2. Начертите окружность радиусом 10 см. Определите момент касательной силы, приложенной к любой точке обода относительно центра окружности. Определите момент силы, которая лежит на нормали к любой точке обода окружности, относительно центра окружности.
4.4 Момент силы относительно оси
Чтобы найти момент силы относительно, например оси z, нужно найти проекцию  этой силы на плоскость, которая перпендикулярна этой оси и проходящей через точку относительно которой находится момент силы относительно точки (см. рис. 42). Затем продолжить линию действия проекции силы
этой силы на плоскость, которая перпендикулярна этой оси и проходящей через точку относительно которой находится момент силы относительно точки (см. рис. 42). Затем продолжить линию действия проекции силы  и найти плечо h от точки О до линии действия проекции силы. Получить рычаг проекции силы относительно оси z, проходящей через точку О.
и найти плечо h от точки О до линии действия проекции силы. Получить рычаг проекции силы относительно оси z, проходящей через точку О.

Рис. 42
Момент силы относительно оси равен произведению проекции силы на плоскость, перпендикулярную этой оси и кратчайшего расстояния от точки, проходящей через ось до линии действия проекции силы, взятое со знаком «+» или «-».
 (1)
(1)
В этой формуле с правой стороны есть два множителя, если хотя бы один из множителей равен нулю, то ответ равен нулю. Рассмотрим эти частные случаи (см. рис. 43):
1. Момент силы относительно оси равен нулю  если линия действия силы
если линия действия силы  параллельна оси, т.е.
параллельна оси, т.е.  =0
=0
2. Момент силы относительно оси равен нулю  если линия действия силы
если линия действия силы  пересекает ось, т.е. h=0.
пересекает ось, т.е. h=0.
Рис. 43
Задание 1.
Круглая горизонтальная платформа вращается вокруг вертикальной оси вращения, имеются опоры: подпятник А и подшипник В соответственно внизу и вверху оси z, так, чтобы ось имела заданное положение (см. рис. 44). Определите моменты реактивных сил этих опор А и В относительно оси z. Определите момент силы тяжести  относительно оси z.
относительно оси z.
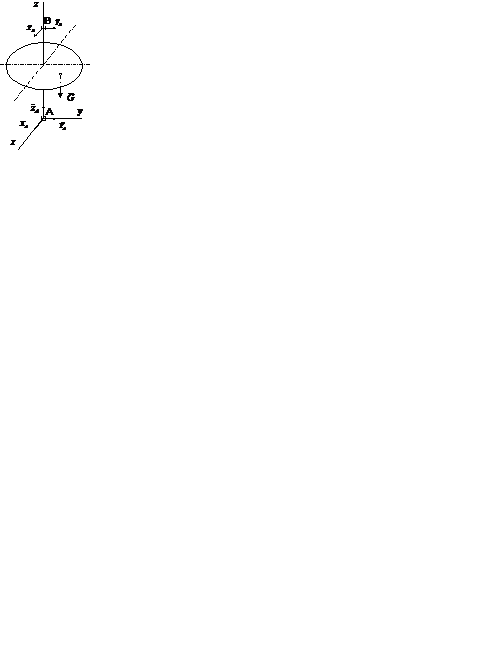 Если вы не можете найти, то постарайтесь разобраться в этой записи:
Если вы не можете найти, то постарайтесь разобраться в этой записи:
 ,
,
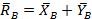
Они являются реакциями опоры А -подпятника и опоры В - подшипника, (точки А и В лежат на оси z). Отсюда линии действий реактивных сил пересекают ось z. Следовательно, моменты реактивных сил
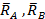 относительно оси z
относительно оси z
Рис. 44 равны нулю

.Что касается силы тяжести  , то линия действия этой силы параллельна оси z. Следовательно, момент этой силы тяжести относительно оси z тоже равен нулю
, то линия действия этой силы параллельна оси z. Следовательно, момент этой силы тяжести относительно оси z тоже равен нулю 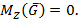
Задание 2.
Самостоятельно найдите моменты сил  , показанных на рис.45 относительно осей x, y, z.
, показанных на рис.45 относительно осей x, y, z.
Для выполнения этого задания вначале рассмотрим силу 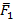 . Рассмотрим расположение заданной силы. Сила расположена в горизонтальной плоскости, разложим её на проекции
. Рассмотрим расположение заданной силы. Сила расположена в горизонтальной плоскости, разложим её на проекции  , (см. рис. 46), используя правило параллелограмма.
, (см. рис. 46), используя правило параллелограмма.
Рис. 45
 Затем нужно определить синус и косинус угла
Затем нужно определить синус и косинус угла 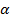 между осями х и у
между осями х и у 
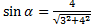 ,
,  .
.
Определим момент силы 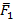 относительно осей x, y, z:
относительно осей x, y, z:


Рис.46
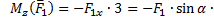 3
3
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 499; Нарушение авторских прав?; Мы поможем в написании вашей работы!