
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Опоры и их реакции
|
|
|
|
Мы знаем, что пространство является трехмерным, а плоскость является - двухмерной. Попытаемся определить количество степеней свободы у свободного тела. В пространстве тело имеет свободное одновременное перемещение относительно трех взаимно-перпендикулярных осей, также имеет свободный одновременный поворот относительно трех тех же осей. Следовательно, тела имеет шесть степеней свободы в пространстве и три на плоскости: два одновременных перемещения относительно двух перпендикулярных осей и поворот тела относительно точки.
Рассмотрим разные крепления тела или виды опор.
1. НЕПОДВИЖНЫЙ ШАРНИР
Внешний вид этой опоры см. на рис.16, а, е соответственно в пространстве и на плоскости. Другое название этой опоры в пространстве - сферический шарнир. Имеем тело А с такой опорой (см. рис.16, а) в пространстве. Используем аксиому освобождаемости от связей. Эта опора имеет ограничение в движении относительно перпендикулярных осей x, y, z, поворот тела относительно трех этих осей возможен.
Например, колпачок авторучки, прикрепленный к письменному прибору или к стенке в почтовом отделении. Колпачок, как тело может поворачиваться относительно трех взаимно перпендикулярных координатных осей в пространстве, в плоскости имеет поворот относительно точки или шарнира А опоры (см. 16е).
а б
в г
е ж
Рис.16
Рис. 17
Реакция неподвижного шарнира в пространстве А равна векторной сумме её проекций:
 (1)
(1)
Модуль и направление реакции опоры А определяются по формулам (1а), (1б):
 (1а)
(1а)
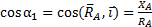
 (1б)
(1б)

Реакция неподвижного шарнира в плоскости имеет две взаимно перпендикулярные составляющие, т. к. в плоскости имеем две взаимно перпендикулярные оси х и y. Эту опору в плоскости называют цилиндрической шарнирно-неподвижной опорой.
Реакция опоры А равна векторной сумме её проекций:
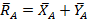 (2)
(2)
Модуль и направление реакции см формулы (2а), (2б), получаем:
 (2а)
(2а)

(2б)
Задание.
Убрать опору на рис. 17, заменить её составляющими реакции опоры. Используйте аксиому освобождаемости от связей и составьте расчетную схему.
2. ПОДВИЖНЫЙ ШАРНИР ИЛИ КАТОК
Внешний вид этой опоры в пространстве имеет вид см. рис.17 а.
а б в
Рис. 17
а б
Рис. 18
Пусть тело В имеет опору- подвижный шарнир или каток. Используем аксиому освобождаемости от связей. Эта опора не имеет ограничения в движении по неподвижной поверхности, проходящей по оси y (см. рис.17 б), но имеются ограничения перпендикулярно направлению движения катка вниз: по оси z, и перпендикулярно направлению движению катков, по оси х,
поворот в шарнире В возможен относительно трех осей x, y, z. Реактивная составляющая по вертикали направлена в обратную сторону давлению катка на поверхность всегда.
Поэтому каток имеет две составляющие реактивной силы
 ,
, 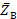 (см.рис.17 б, в).
(см.рис.17 б, в).
Реакция опоры В равна векторной сумме её проекций:
 (1)
(1)
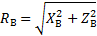 (1а)
(1а)

(1б)

На плоскости на рис.18 а показан внешний вид катка и её реакция  , которая перпендикулярна этой поверхности и направлена в обратную сторону давлению.
, которая перпендикулярна этой поверхности и направлена в обратную сторону давлению.
на рис.18 б показана опора на наклонной неподвижной поверхности с её реакцией 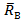 , которая имеет две составляющие
, которая имеет две составляющие
 , где
, где
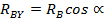 ,
,  sin
sin 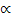 .
.
3. ГЛАДКАЯ ПОВЕРХНОСТЬ
Гладкой поверхностью называется опора, которая является абсолютно гладкой и не имеет шероховатости. Это значит, что микронеровности на поверхности отсутствуют. Для неё коэффициент трения скольжения равен нулю. Гладкая поверхность мешает перемещаться телу в любом направлении. Для определения реакции гладкой поверхности должно быть давление тела на поверхность. Например, это может быть сила тяжести тела. Реакция или реактивная сила гладкой поверхности направлена перпендикулярно поверхности и ориентирована в обратную сторону давлению тела на поверхность. На каждом рис. 19 а, б, в, показана гладкая опора и её реакция 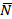 . На рис.19 г показаны две гладкие поверхности – горизонтальная и наклонная, на которые опирается тело в точках А, В. Реакции
. На рис.19 г показаны две гладкие поверхности – горизонтальная и наклонная, на которые опирается тело в точках А, В. Реакции  ,
,  соответственно направлены перпендикулярно этим поверхностям в обратные стороны давлению на каждую поверхность.
соответственно направлены перпендикулярно этим поверхностям в обратные стороны давлению на каждую поверхность.
Задание.
Найдите составляющие реакции гладкой поверхности на координатные оси для рис. 19 б, рис. 19 г соответственно
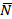 ,
,  , если угол наклона с горизонтом равен
, если угол наклона с горизонтом равен 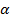 .
.
а
б
в
г
Рис. 19
4. СТЕРЖЕНЬ
 Невесомый стержень это тело, имеющее один размер–длину, связан с другими телами. Стержень рассматривается в пространстве или в плоскости. Эта опора может быть не в единственном числе связана с другим телом, другими телами. Например, плоская ферма- соединение стержней, применяемая для покрытия кровли домов, всевозможные решетки, перегородки у мостов и т.д. (см.рис. 20).
Невесомый стержень это тело, имеющее один размер–длину, связан с другими телами. Стержень рассматривается в пространстве или в плоскости. Эта опора может быть не в единственном числе связана с другим телом, другими телами. Например, плоская ферма- соединение стержней, применяемая для покрытия кровли домов, всевозможные решетки, перегородки у мостов и т.д. (см.рис. 20).

Рис. 20
Реакция стержня направлена вдоль стержня, т.к. ограничивает движение тела именно в этом направлении. Поэтому реактивную силу стержня нужно направить вдоль стержня от тела. На этом рис. 21 а показана стержневая система, состоящая из двух узлов А и В и пяти стержней. На рис.21, б показана её расчетная схема для узла А, для узла В и реакциями пяти стержней 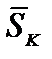 , где к=1,2,3,4,5..
, где к=1,2,3,4,5..
а б

Рис. 21
Задание.
1.Самостоятельно составить расчетную схему для рис. 22 а.
2. Для рис. 22 б составить расчетные схемы для узлов А и В.
3. Для рис. 22 б составить расчетные схемы для узлов D, E, где находятся опоры стержневой системы.
а б
Рис. 22
5. НИТЬ
Опора-нить является гибкой связью и ограничивает движение тела вдоль нити. Заменяем нить реакцией, которая направлена вдоль нити от тела. Реакцию нити можно назвать любой латинской прописной буквой кроме 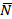 , которой обозначается реакция гладкой поверхности, например буквой
, которой обозначается реакция гладкой поверхности, например буквой  , реакция нити по-другому называется силой натяжения нити. Например, груз висит на тросе (см. рис. 23 а) или рассматриваем линии передач (см. рис. 24),
, реакция нити по-другому называется силой натяжения нити. Например, груз висит на тросе (см. рис. 23 а) или рассматриваем линии передач (см. рис. 24),
а б а

б
Рис. 23 Рис. 24
где показаны связи и расчетные схемы равновесие тела-груза (см. рис. 23, б) и равновесие узла В (см. рис. 24, б). Во втором случае траектория нити является не прямая, а кривая, то реакция её направлена от узла В, по касательным к нитям (проводам от столба).
Задание.
Самостоятельно закрепить тело на нитях и составить расчетную схему для своего рисунка.
6. ПОДШИПНИК (Подшипник качения)
Под подшипником подразумевается подшипник качения, который ставится на валу рядом с зубчатым колесом с двух сторон. Эта опора имеет короткие направляющие вдоль оси вала. Любой подшипник имеет две части, одна связана с неподвижным объектом, другая часть вращается вместе с валом. В подшипнике качения промежуточным звеном между обеими её частями являются или шарики, или ролики, или иголки. Назначение подшипника – поддерживать заданное направление вала с помощью неподвижной её части, а подвижная часть подшипника вращается с валом с незначительным трением (см. рис. 25). Считаем, что подшипники А и В могут свободно перемещаться вдоль оси вала (по оси у), но по другим осям x и z они не смогут двигаться. Тогда реактивная сила имеет составляющие по осям x и и z.
а
Рис. 25
Поворот подшипника вдоль трех взаимно-перпендикулярных осей возможен. По формулам (1), (2), (3), (4) находятся модули и направления реактивных сил для опор А и В (см. рис. 26), где показана расчетная схема:
Вектор реакции опоры А равен геометрической сумме её составляющих:
 (1)
(1)
Рис. 26
 (1а)
(1а)
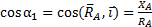
(1б)

 (2)
(2)
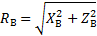 (2а)
(2а)

(2б)
Задание.
1. Дан вертикальный вал. Прикрепите к нему опоры, но так, чтобы одна из опор была подшипником и вал был в вертикальном направлении.
2. Уберите опоры и замените их реактивными силами, т.е. составьте расчетную схему для вертикального вала.
7. ПОДПЯТНИК (Подшипник скольжения)
Подпятником называется подшипник скольжения, пята, или цапфа. Ставится подпятник в конце вала для того, чтобы вал не имел смещения вдоль своей оси. Возникает такое смещение в зубчатой косозубой передаче, когда результирующая сила, действующая от ведущей шестерни другом валу, передает окружную силу, радиальную силу и осевую силу данному колесу, показанному на рис. 25. Осевая сила действует на перемещение вала вдоль неё, поэтому данная опора-подпятник не дает смещения вала вдоль оси у. Представляет собой «стакан», у которого очень небольшая высота, дно «стакана» является ограничителем движения вала, а «стенки стакана» направлены вдоль вала. Опора препятствует смещению вала вдоль трех взаимно-перпендикулярных осей, считается, что поворот тела в опоре возможен относительно трех взаимно перпендикулярных координатных осей. Реакция от подпятника имеет три взаимно-перпендикулярные составляющие. На рис. 25 показаны эти опоры D и E - подпятники, их реакции по модулю и направлению находятся по аналогии с неподвижным шарниром, например, для опоры D (см. рис 26):
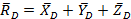 (1)
(1)
 (1а)
(1а)

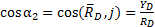 (1б).
(1б).
Реакции для опоры Е находятся по аналогии.
Задание.
Самостоятельно записать модуль и направление реакции опоры Е.
8. ЖЕСТКАЯ ЗАДЕЛКА
Такая опора абсолютно ограничивает движение тела в пространстве и не дает смещаться и поворачиваться. Результирующее поступательное движение этой плиты можно разложить на движения вдоль трех взаимно перпендикулярных осей вдоль взаимно-перпендикулярных осей, x, у, z. Плита не имеет возможности поворачиваться вокруг мгновенной оси 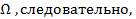 не может поворачиваться относительно этих же осей. x, у, z.
не может поворачиваться относительно этих же осей. x, у, z.
Примером может быть балконная плита, жестко заделанная в стену здания (см. рис.27 а). Опора имеет два
элемента – реактивную силу и реактивный момент. Они представлены через три составляющие реактивной силы, ориентированные по осям x, y, z и три составляющие реактивного момента относительно этих же осей.
 (1)
(1)
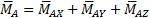 (2)
(2)
Реакции силы 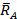
 и момента
и момента 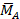 по модулю и направлению см. по (1а), (1б), (2а), (2б) соответственно.
по модулю и направлению см. по (1а), (1б), (2а), (2б) соответственно.
На плоскости тело с опорой – жесткая заделка, у которой нет перемещения относительно двух взаимно-перпендикулярных осей и поворота тела относительно любой точки его тела реакции силы 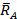 и момента
и момента 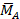 см. по формулам (3), (4).
см. по формулам (3), (4).
а
б
в
Рис. 27
 (1a)
(1a)
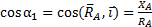
 (1б)
(1б)

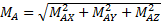 (2а)
(2а)

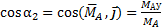 (2б)
(2б)
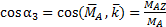
Формулы определения величин реактивных сил жесткой заделки в плоскости:
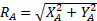 (3а)
(3а)
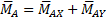 (4а)
(4а)
 (3б)
(3б)
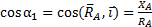
(3в)

 (4б)
(4б)

(4в)
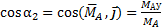
Задание.
1. Для рис. 27 б написать реактивные силу и момент в опоре А как векторные суммы её составляющих.
2. Написать для рис. 27 в реактивную силу и реактивный момент в опоре, а также модули их и направления реакций как векторов.
3. Начертить рисунок в плоскости, где показана крепление - жесткая заделка на вершине С треугольника АВС, считая сторону ВС горизонтальной. Показать реакции в опоре и написать их по подобию (см. пред. п. задания).
4. Стройплощадка. Кладка стены из кирпича. Объясните какие связи существуют у кирпича в выполненной стене.
9. СКОЛЬЗЯЩАЯ ЗАДЕЛКА
Опора представляет собой гладкую втулку насаженную на тело, которым является гладкий стержень (см рис. 28, а). Втулку можно заменить длинными направляющими (см. рис. 28, б), направить координатные оси показать реактивные силы (см. рис. 28, в).
По оси у движение стержня свободно, а также его поворот относительно этой оси у. Отсюда реактивные силы закрывают перемещение стержня вдоль осей x и z и поворот относительно этих же осей x и z их реакции как векторы равны:
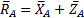 (1)
(1)
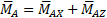 (2)
(2)
Модули и направления реактивной силы  и реактивного момента
и реактивного момента 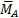 находятся по формулам (1а), (1б), (2а), (2б):
находятся по формулам (1а), (1б), (2а), (2б):
 (1а)
(1а)
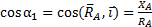
(1б)

 (2а)
(2а)

(2б)
а б
в
Рис.28
а б
в г
Рис.29
Рассмотрим эту опору- скользящую заделку в плоскости, их два типа (см.рис. 29, а, б).
Рассмотрим первый тип. Плоское тело в форме бруса свободно перемещается относительно оси х по направляющим. Следовательно, перемещение вдоль оси, которая перпендикулярна направляющим отсутствует, поворота бруса относительно точки А тоже нет из-за длинных направляющих. Отсюда реактивная сила направлена по перпендикуляру к направляющим  и реактивный момент относительно точки А равен
и реактивный момент относительно точки А равен  .
.
Рассмотрим второй тип скользящей заделки на плоскости. Дан брус, у которого шарнирно прикреплен стержень, (см. рис. 29 в). Этот брус вместе со стержнем и вертикальными направляющими стержня может свободно перемещаться вдоль горизонтальных направляющих, направленных по длине бруса. Также брус вместе с горизонтальными направляющими может свободно перемещаться вдоль вертикальных направляющих стержня, шарнирно связанного с брусом. Отсюда вывод, стержень имеет свободное перемещение вдоль взаимно перпендикулярных осей х, у, но не может поворачиваться относительно точки А из-за длинных направляющих. Для данной опоры есть одна реакция- это реактивный момент относительно этой точки 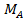 (см. рис. 29 г).
(см. рис. 29 г).
Задание.
1. Начертить тот же брус (см. рис. 29 в, г)на плоскости под углом 300 к горизонту, назвать её опорой D.
2. Приложить к опоре D (см. п.1 задания) скользящие заделки первого и второго типов.
3. Составить расчетные схемы для случаев 1, 2.
4. Аквапарк. Движение человека по лабиринту. Объясните связи при движении человека по лабиринту.
5. Санный спорт или бобслей. Экипаж состоит из четырех человек. Объясните связи при движении экипажа по лабиринту.
10. ПЕТЛЯ
а б
в
Рис. 30
Опора – петля по размерам много меньше чем само тело. С помощью такой опоры крепятся подвижные к неподвижному корпусу. Например. Крепление оконных рам к косяку, крепление дверей к неподвижному косяку. Крышка ноутбука к неподвижному корпусу, крышка шкатулки к своему основанию, крышка чемодана к своему корпусу и т. д. Ограничение подвижных частей при креплении к неподвижной части находится в плоскости, в которой движется подвижная часть при открывании и закрытии объекта - неподвижной части. Таким образом, реактивная сила или реакция имеет две составляющие на координатные оси в плоскости работы подвижной части. Поскольку сама петля мала по сравнению с подвижной и неподвижной частями, то ограничение в повороте относительно осей, по которым имеются составляющие реакции опоры, отсутствует.
На рис. 30 а показаны петли как опоры в точках А и В, которые крепят крышку к неподвижному корпусу. Крышка может работать в плоскости. В которой находятся оси z, y. На рис.30 б показаны составляющие реакций опор-петель в точках А и В:
 (1)
(1)
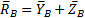 (2)
(2)
Задание.
1. Написать модули реакций в опорах А и В.
2. Написать направления реактивных сил  ,
, 
11.УГОЛ или НЕПОДВИЖНАЯ ТОЧКА
Тело опирается на неподвижную точку или угол. В этом месте существует ограничение, которое направлено перпендикулярно касательной к неподвижной точке, т.е. направлено ограничение по нормали, следовательно, реакция связи направлена по нормали к неподвижной точке от точки.
а б
в
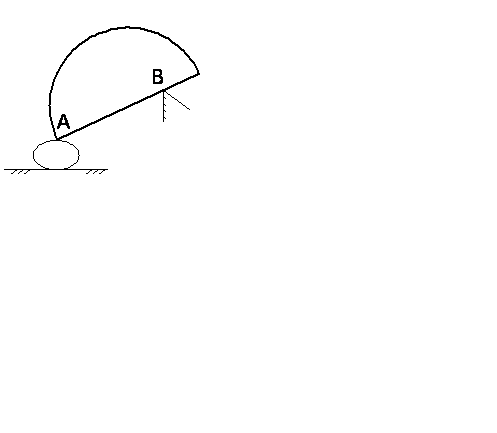
Рис. 31
На рис. 31 а показано тело, которое опирается на неподвижные точки A, В, и С. Видно, если опора - угол, то реакция перпендикулярна касающегося поверхности тела, если опора - неподвижная точка представляет в точке касания кривую, то следует представить касательную и провести нормальную ось, перпендикулярную ей, по ней провести реакцию как это показано на рис, 31 б, т.е. по аксиоме освобождаемости от связей убрали опоры и заменили их реакциями связей.
Задание.
1. На рис. 31в самостоятельно использовать аксиому освобождаемости от связей.
2. Представьте себе статуэтку, скульптуру, на которой изображен человек, стоящей на одной ноге. Как называется эта работа? На каком принципе она выполнена?
3. Другой пример. Скульптура «Медный всадник», что стоит на Исаакиевской площади. На каком принципе она выполнена?
12. СИЛА ТРЕНИЯ
А. Сила трения скольжения.
а в


г д


Рис. 32
Трение – это физическое явление, является неизбежным спутником, оно является неизбежным спутником перемещения тел в сопротивляющейся среде.
Оно присутствует всюду, что окружает человека: в воде, в воздухе, на земле. Это явление рассмотрим подробно в теме «Трение». А сейчас, забегая немного вперед, рассмотрим трение скольжения и трение качения.
Трение скольжения сопровождается при поступательном движении тела. Величина силы трения зависит от физических свойств соприкасающихся поверхностей: от материала и степени шероховатости их.
Сила трения скольжения по модулю равна
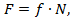 (1)
(1)
где f есть коэффициент трения скольжения и является безразмерной величиной, 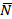 реакция давления тела на поверхность, см. опору - гладкая поверхность. Если же движения нет, то она называется сила трения сцепления и величина её равна
реакция давления тела на поверхность, см. опору - гладкая поверхность. Если же движения нет, то она называется сила трения сцепления и величина её равна
 , (2)
, (2)
где fсц есть коэффициент трения сцепления, причем
fcц > f, (3)
т.к. сила трения сцепления больше чем сила трения скольжения. А если рассматривать движение тел, то сила трения является зависимой от скорости тела, чем больше скорость, тем меньше сила трения.
Направление силы трения зависит от того является ли тело ведущим или ведомым звеном. Например, при ходьбе человека сила трения скольжения направлена по движению, а, если рассматривать ведомое звено, например,
зимой движение саней, то сила трения направлена в обратную сторону его движению.
В покое сила трения препятствует попытке переместить тело.
На рис. 32 а показано определение реакции нормали 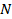 , которая находиться из условия, что движение по оси у отсутствует. В данном случае на движение тела влияет сила
, которая находиться из условия, что движение по оси у отсутствует. В данном случае на движение тела влияет сила 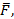 которая расположена под углом
которая расположена под углом 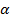 к горизонту, поэтому её проекция на ось у влияет на величину реакции
к горизонту, поэтому её проекция на ось у влияет на величину реакции 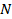 нормали. Сила трения находится при движении по формуле (1), при покое по формуле (2). На рис.32 б показана направление силы трения и её величина. Рассмотрим покой.
нормали. Сила трения находится при движении по формуле (1), при покое по формуле (2). На рис.32 б показана направление силы трения и её величина. Рассмотрим покой.
Рассмотрим рис.32 в. Поскольку тело находится на наклонной поверхности, тело может переместиться вниз, т.к. на её перемещение может влиять проекция силы трения на наклонную поверхность. Поэтому сила трения направлена в обратную сторону возможному движению тела, равна см. рис. 32 г, её величина также найдена по формулам (1) или (2), что показано под этим рисунком.
Задание.
1.Самостоятельно придумайте ситуацию, где объект находится в покое, а его пытаются сдвинуть, но еще не сдвинули.
2. Определите величину и направление силы трения
Б. Сила трения качения
Трение качения возникает в результате деформации катящегося колеса и опорной поверхности. Считаем, что колесо тело твердое, а поверхность нетвердая, которая покрыта не бетоном и не асфальтом, например, имеется грунтовая дорога (см. рис. 33 а).
Тогда реакция гладкой поверхности 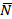 находится не по
находится не по
центру колеса, а на расстоянии  , коэффициента трения качения, от силы тяжести
, коэффициента трения качения, от силы тяжести  , так чтобы обе силы составляли пару с моментом трения качения
, так чтобы обе силы составляли пару с моментом трения качения
 , направленного в обратную сторону вращению колеса. На рис. 33 б показано движение колеса по горизонтали и определение момента трения качения. На рис. 34 а, б показано движение колеса по наклонной поверхности и определение момента трения качения.
, направленного в обратную сторону вращению колеса. На рис. 33 б показано движение колеса по горизонтали и определение момента трения качения. На рис. 34 а, б показано движение колеса по наклонной поверхности и определение момента трения качения.

а
б
Рис.33
а б
Рис. 34
Если рассмотреть движение тела как колеса, то мы видим поступательное движение центра колеса и вращение всех точек тела вокруг центра. На рис. 33 показано качение колеса (вращение) без скольжения (нет силы трения) при движении. На рис. 34 показано движение колеса по наклонной поверхности со скольжением и с качением. Если колесо рассматривать в статике, то движение колеса отсутствует, но силы, действующие на колесо, уравновешиваются.
Задание.
1. Самостоятельно придумать ситуацию: тело находится в плоскости; на него действует одна известная сосредоточенная сила под острым углом к горизонту и распределенная нагрузка с постоянной интенсивностью; закрепить с телом любые три разные по виду опоры.
2. Направит координатные оси.
3. Применить аксиому освобождаемости от связей для составления расчетной схемы.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 3410; Нарушение авторских прав?; Мы поможем в написании вашей работы!