Дисперсия. Среднее линейное отклонение

Среднее линейное отклонение

Среднее линейное отклонение представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической величины.

В формулах разности в числителе взяты по модулю (иначе в числителе всегда будет ноль – алгебраическая сумма отклонений вариантов от их средней арифметической величины)

Поэтому среднее линейное отклонение как меру вариации признака применяют в статистике только в тех случаях, когда суммирование показателей без учета знаков имеет экономический смысл. С его помощью, например, анализируется состав работающих, ритмичность производства, оборот внешней торговли.

Дисперсия это средний квадрат отклонений индивидуальных значений признака от их средней величины.

Для вычисления дисперсии иногда удобнее использовать формулу разности квадратов:

,

Распишем:

,

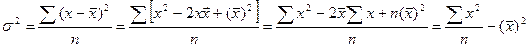то есть дисперсия равна разности средней из квадратов значений признака 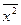и квадрата средней арифметической . При использовании этой формулы исключается дополнительная процедура расчета отклонений индивидуальных значений признака от и ошибка в расчете, связанная с округлением отклонений (х_i - ).

Свойство дисперсии

1.) дисперсия постоянной величины равна нулю;

2.)если все варианты значений признака уменьшить на одно и то же число, то дисперсия не уменьшится;

3.)если все варианты значений признака уменьшить в одно и то же число раз (k раз), то дисперсия уменьшится в k² раз;

4.)Средний квадрат отклонений от любой величины А определяется по формуле:

.

Дата добавления: 2015-06-25