Применение модуля нечеткого управления для прогнозирования случайных временных рядов

ипй, ^Прог.^нозиР°^вание временных рядов считается чрезвычайно важ­ной задачей, возникающей в области экономики, финансового планиро­вания, управления производством, предсказания погоды обработки сиг­налов, управления в технических системах и т.п В настоящем под­разделе будет моделироваться поведение модуля нечеткой _Упра2-ГмЭ г? ^В?^{ЭДаЧе п}Р°^гнозиР^ования временного ряда Маккея-Гласса (Mackey-Glass), который описывается дифференциальным уравнением

200 400 600

Рис. 5.5. Хаотический процесс Маккея-Гла

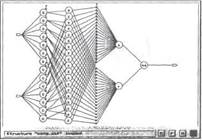
При t > 17 рассматриваемый ряд ведет себя хаотически. Чем боль­ше значение t, тем более хаотичным становится характер ряда Для мо­делирования установим t = 30. На рис. 5.5 представлен поимео оазвития процесса для 1000 точек ряда Маккея-Гласса.^ДДопустим"чтГпер^Рвые7™ ЖЙ5Г ^{использоваться в каче}стве обучающей выборки, а последние 300 точек - в качестве тестовых данных. На рис. 5.6 представлена ctdvk-тура модуля нечеткого управления. Он построен на базе 19 правил пред­ложенных экспертом. Эти правила можно сформулировать и другими способами - например, методом, описанным в разд 3.10. Форма фикции принадлежности для обоих входных сигналов показана на рис 5 7 %а нем используются следующие обозначения: N - отрицательный ZE - hv-левои, Р - положительный). На первый вход подается значение ряда в момент t, а на второй вход - значение в момент t- 1 Задача модуля йе четкого управления заключается в определении значения ряда в момент

После проведения моделирования выяснилось, что предсказыва­емые значения сильно отличаются от тестовых данных (см. рис 5 8) По­этому модуль был подвергнут обучению. Как уже отмечалось, в качестве обучающей выборки использовались первые 700 значений временного ряда. На рис. 5.9 представлены два варианта процесса обучения сети: а) когда обучающая последовательность предъявлялась строго последо­вательно и б) когда обучающие данные выбирались случайным образом 11редставленная на рисунке мера погрешности была задана в алгоритме обратного распространения ошибки формулой

■

Рис. 5.6. Структура модуля временных рядов.

управления, применяемого для прогнозирования

Глава 5. Модули нечетко-нейронного управления

5.1. Определение структуры модуля управления при дефуззификации 325 2.00 -■

Сеть, обученная случайным образом Сеть, обученная последовательно

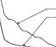
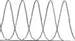
Рис. 5.7. Исходные функции принадлежности: а) первый вход; б) второй вход.

Рис. 5.8. Тестирование модуля нечеткого управления до начала обучения.

Рис. 5.9. Процесс обучения модуля нечеткого управления с помощью алгоритма обратного распространения ошибки.

А
	УШк 1
-S.W	2.»

Рис. 5.10. Функции принадлежности по завершении обучения.

Глава 5 Модули нечетко-нейронного управления

5.1. Определение структуры модуля управления при дефуззификации

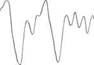
Рис. 5.11. Тестирование модуля нечеткого управг

о завершении обучения.

зовать пять функций принадлежносги, а для второго входного сигнала -угла ф, под которым грузовик находится к оси у - семь функций принад­лежности. В результате генерации посылок нечетких правил на основе попарного сопоставления всех функций принадлежности первой и второй переменной олучено 5 х 7 = 35 правил. Модуль нечеткого управления, созданный на базе этих правил, представлен на рис. 5.12. Функции при­надлежности для входных переменных были равномерно р с ределены так, как это показано на рис. 5.13. Центры функции принадлежности вы­ходной переменной (угла поворота колес грузовика в) размещены в точ­ке 0, что равнозначно отсутствию выводов (заключений) в правилах Сформированные таким образом исходные функции принадлежности ис­пользовались в модуле нечеткого управления путем задания соответст­вующих начальных значений параметров и весов.

В процессе обучения модуля применялись те же обучающие дан­ные, что и в п. 3.10.2. На протяжении первых 38 эпох сеть обучалась с по­мощью стандартного алгоритма обратного распространения ошибки с ко­эффициентом обучения г] = 0,25. Следующие 70 эпох сеть обучалась по тому же алгоритму, однако значе е коэффи иента обучения автомати­чески уменьшалось (до уровня ц = 0,1). Процесс обучения иллюстрирует­ся на рис. 5.14 (функция погрешности представлена в логарифмическом масштабе).

Откорректированные в процессе обучения функции принадлежно­сти показаны на рис. 5.15. Центры функции принадлежности выходной переменной, полученные в результате обучения, приведены на рис. 5.16.

где у - выходной сигнал модуля нечеткого управления, ad - эталонный сигнал. Обучение проводилось на протяжении 30 эпох.

Тот факт, что последовательность предъявления обучающих дан­ных имеет существенное значение, не является неожиданным. Интере­сно то, что обучение нечетко-нейронной сети данными, предъявляемыми строго последовательно, в начальной фазе оказывается значительно бо­лее эффективным. Аналогичный эффект зарегистрирован и при прове­дении других экспериментов.

На рис. 5.10 представлены функции принадлежности по заверше­нии обучения. Они довольно сильно отличаются от исходных, которые были предложены экспертом (рис. 5.7). Конечно, количество правил, рав­ное 19, в процессе обучения оставалось неизменным. Результаты тестирования обученного модуля нечеткого управления представлены графиком на рис. 5.11.

Дата добавления: 2015-06-04