Расчет ферм

Если число стержней и число узлов фермы удовлетворяет данному условию, то ферма является статически определимой, т.е. число независимых уравнений статики достаточно для определения усилия в каждом стержне. Простая ферма всегда статически определима.

Если S >2 n -3 - ферма (рис.8.4) статически неопределима.

Если S <2 n -3 - ферма (рис.8.5) неустойчива, т.е. конструкция получается подвижной (ферма становиться механизмом).

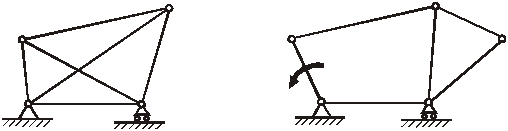
Рис.8.4 Рис.8.5

Кинематикой называется раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.

Основная задача кинематики точки и твердого тела состоит в том, чтобы, зная закон движения точки (тела), установить методы определения всех кинематических величин, характеризующих данное движение.

СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ

Для задания движения точки можно применять один из следующих способов: векторный, координатный, естественный.

Векторный способ задания движения точки

Пусть точка М движется по отношению к некоторой системе отсчета Охуz.

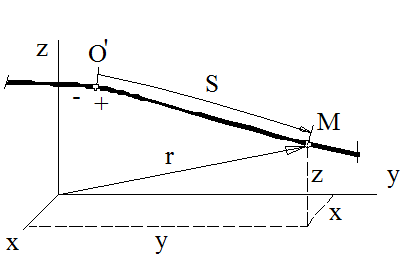
Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор , проведенный из начала координат О в точку М.

При движении точки М данный вектор будет с течением времени изменяться и по модулю, и по направлению. Следовательно, он является переменным вектором (вектором-функцией), зависящим от аргумента t - времени:

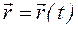
Это равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий радиус-вектор и найти положение движущейся точки. Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. Если траекторией является прямая линия, движение точки называется прямолинейным, а если кривая - криволинейным. Геометрическое место концов радиуса-вектора, т. е. годограф этого вектора, определяет траекторию движущейся точки.

Координатный способ задания движения точки

Аналитически, как известно, вектор задается его проекциями на координатные оси. В прямоугольных декартовых координатах для радиуса-вектора будет справедливо следующее:

r_x=x; r_y=y; r_z=z,

где х; у; z - декартовы координаты точки (Рис.2.1). Т.е. положение точки в пространстве можно определить и ее декартовыми координатами. Если ввести единичные векторы (орты) 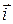, , 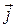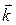координатных осей, получим для радиуса-вектора выражение

.

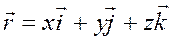Если вместо зависимости 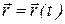будут заданы координаты х, у и z точки как функции времени

,

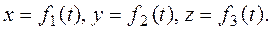то такой способ задания движения точки будет называться координатным.

Если движение точки происходит все время в одной и той же плоскости, то, приняв эту плоскость за плоскость Оху, получим в этом случае два уравнения движения:

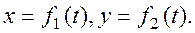
Наконец, при прямолинейном движении точки, если вдоль ее траектории направить координатную ось Ох, движение будет определяться одним уравнением

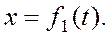
Описанные выше уравнения представляют собой одновременно уравнения траектории точки в параметрической форме, где роль параметра играет время t. Исключив из уравнений движения время t, можно найти уравнение траектории в координатной форме, т.е. в виде, дающем зависимость между координатами точки. Например:

.

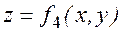Естественный способ задания движения точки

Естественным (или траекторным) способом задания движения точки удобно пользоваться в тех случаях, когда траектория движущейся точки известна заранее. Например, заранее известна траектория кабины лифта, железнодорожного вагона, движущегося по рельсам и т.д.

Т.е. естественный способ описания движения тесно связан с человеческой деятельностью, вытекает из практической потребности рассмотрения перемещений по железным и автомобильным дорогам, по рекам и т.п.

При задании движения естественным способом необходимо введение особых осей. Эти оси, называемые осями естественного трехгранника (естественными или скоростными осями).

Введем предварительно некоторые понятия для определения направления указанных осей.

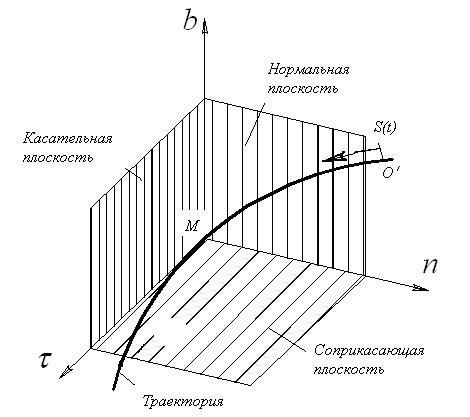
Пространственную кривую, представляющую собой траекторию движения точки, можно разбить на элементарные участки. На каждом элементарном участке пространственная кривая может быть представлена в виде плоской кривой. Сама плоскость, к которой бесконечно близко расположены точки элементарного участка пространственной кривой, называется соприкасающейся плоскостью.

В случае плоской кривой соприкасающейся плоскостью для всех ее точек является плоскость, в которой лежит сама кривая.

Перпендикулярно соприкасающейся плоскости расположены касательная и нормальные плоскости.

Направление касательной плоскости определяется направлением касательной в рассматриваемой точки кривой (точка М). Нормальная плоскость перпендикулярна также касательной плоскости.

Направлены естественные оси следующим образом:

ось M 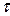— по касательной к траектории в сторону положительного отсчета расстояния s, называется касательной осью;

ось Мп — по нормали к траектории, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории, называется главной нормалью;

ось Mb — перпендикулярно к первым двум так, чтобы она образовала с ними правую систему осей, называется бинормалью

Т.е. движение точки считается описанным естественным способом, если для неё определены (Рис.2.2): траектория, координата 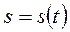вдоль траектории, измеренная в линейных единицах, определяющая длину дуги от начала отсчета (O ^’) и для определенности необходимо условится о направлении отсчета дуговой координаты 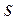(положительное (+) и отрицательное (-) направления).

Заметим, что величина s в уравнении определяет положение движущейся точки, а не пройденный ею путь.

Определение скорости и ускорения точки при векторном способе задания ее движения

Скорость точки равна первой производной от радиуса-вектора этой точки по времени.

Скоростью точки называется вектор, определяющий в каждый момент времени быстроту и направления движения скорости.

Если точка в равные, произвольно взятые промежутки времени проходит одинаковое расстояния, то ее движение называется равномерным, а в противном случае движение точки называется неравномерным или переменным.

вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.

Определение скорости и ускорения точки при координатном способе задания движения

Определение скорости точки. Ранее было получено, что вектор скорости точки 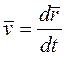. Отсюда на основании вышеуказанной теоремы найдем

v_x = dx/dt, v_y = dy/dt, v_z =dz/dt

Таким образом, проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.

Проекции ускорения точки на координатные оси равны первым производным от проекций скорости или вторым, производным от соответствующих координат точки по времени.

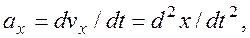
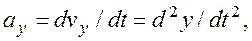
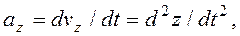
Скорости и ускорение точки при естественном способе задания движения

Числовое значение скорости точки в данный момент времени равно первой производной от расстояния (криволинейной координаты) s этой точки по времени. v = ds/dt

формулы для определения ускорения точки при естественном способе задания её движения:

,

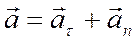где 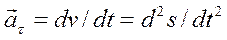- касательная составляющая ускорения

и 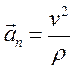- нормальная составляющая ускорения;

a= ,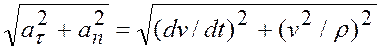

Дата добавления: 2015-06-04