Относительное, переносное и абсолютное движения точки

СВОБОДНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА

Определение ускорений точек плоской фигуры

Ускорение любой точки М плоской фигуры геометрически складывается из ускорения какой-нибудь другой точки А, принятой за полюс, и ускорения, которое точка М получает при вращении фигуры вокруг этого полюса.

Сферическим движением твердого тела называют такое движение при котором одна его точка все время остается неподвижной.

Все точки тела, совершающего сферическое движение, движутся по траекториям, которые располагаются на сферах соответствующего радиуса. Сферически движущееся тело обладает тремя степенями свободы.

Такое движение совершает, например, волчок, у которого неподвижна точка его опоры о плоскость., или любое другое тело, закрепленное в точке О шаровым шарниром.

Свободным движением твердого тела называется такое движение, при котором тело может произвольно перемещаться в пространстве.

Движение, совершаемое точкой М по отношению к подвижной системе отсчета, называется относительным движением. Скорость точки М по отношению к подвижной системе отсчета называется относительной скоростью (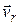), а ускорение - относительным ускорением ().

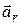Движение, совершаемое подвижной системой отсчета (и всеми, неизменно связанными с нею точками) по отношению к неподвижной системе отсчета является для точки М переносным движением.

Скорость точки, неизменно связанной с подвижными осями и с которой в данный момент времени совпадает движущаяся точка М, называется переносной скоростью точки М в этот момент (). А соответствующее ускорение - переносным ускорением точки М ().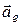

Движение, совершаемое точкой по отношению к неподвижной системе, отсчета называется абсолютным, его скорость - абсолютной скоростью (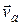) и ускорение - абсолютным ускорением ().

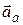абсолютная скорость точки равна векторной сумме ее относительной и переносной скоростей.

Модуль абсолютной скорости

,

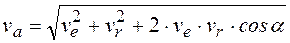где α – угол между векторами относительной и переносной скоростей точки.

.

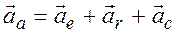Итак, абсолютное ускорение точки равно векторной сумме переносного, относительного и Кориолисова ускорения.

Дата добавления: 2015-06-04