Система сходящихся сил

Лекция 2

Системой сходящихся сил (ССС) называется такая система сил, линии действия которых пересекаются в одной точке.

ССС эквивалентна равнодействующей силе, которая равна векторной сумме слагаемых сил. Точка приложения равнодействующей силы совпадает с точкой пересечения линий действия сил.

Решение многих задач механики связано с операциями сложения сил.

Определение. Вектор, равный геометрической сумме системы сил, называется главным вектором системы сил.

Не путать с понятием равнодействующей!

Главный вектор определяется всегда для любой системы сил. Но существуют системы сил, которые нельзя заменить равнодействующей – пара сил, скрещивающиеся силы.

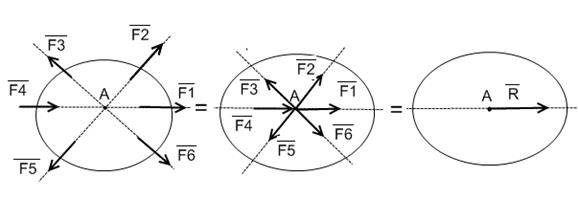
Операции сложения сил и разложение сил на составляющие

1. Сложение двух сил: .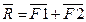

Выполняется по правилу параллелограмма или путем построения силового треугольника.

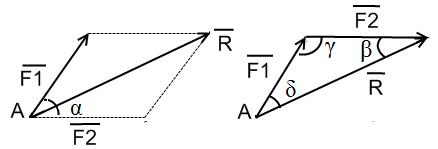
Модуль силы находится с помощью теоремы косинусов или теоремы синусов:

R = ,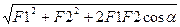

.

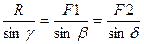2.Сложение трех сил, не лежащих в одной плоскости: .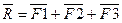

Операция сводится к нахождению диагонали параллелепипеда, построенного на этих силах. В простейшем случае параллелепипед прямоугольный (рис.1-9)

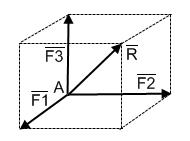
Модуль вектора находим по формуле: .

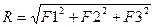3.Сложение системы сходящихся сил: .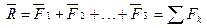

Операция сложения выполняется либо последовательным применением к системе сил правила параллелограмма, либо путем построения силового многоугольника (рис.1-9).

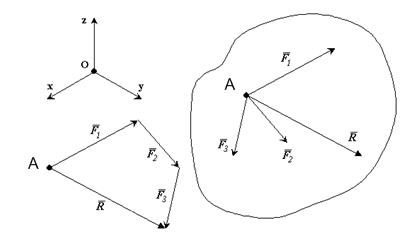
4.Разложение силы на составляющие.

Операция, обратная сложению сил. Может быть выполнена неоднозначно. Необходимо задать направления составляющих сил. Наиболее часто встречаются два случая:

1) Разложение силы на две составляющие: .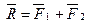

Операция сводится к нахождению сторон параллелограмма, у которого известна диагональ R и углы, образованные с диагональю линиями действиясоставляющих сил. Ниже показаны три варианта разложения силы на составляющие: 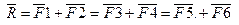. Модули составляющих сил находятся по теореме синусов при известных значениях углов.

2) Разложение силы на три составляющие, не лежащие в одной плоскости:

.

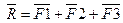Операция сводится к нахождению сторон параллелепипеда, у которого известной является диагональ.

Аналитический способ нахождения равнодействующей ССС

Аналитические методы решения задач механики основаны на методах проекций.

Аналитический способ задания силы.

В декартовых координатах приложенный в заданной точке А вектор 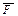можно задать двумя способами.

1) - задать координаты точки А (x,y,z), - задать модуль вектора F, - задать углы α, β, γ, образованные вектором с осями координат.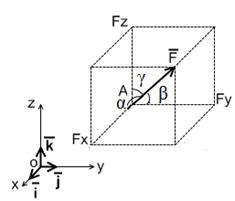

2) - задать координаты точки А (x,y,z),

- определить проекции вектора 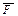на оси координат: Fx, Fy, Fz.

- определить модуль вектора и направляющие косинусы:

F = , .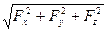

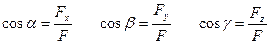Аналитический способ нахождения равнодействующей

Используется теорема геометрии: Проекция вектора суммы на какую-либо ось равна алгебраической сумме проекций слагаемых сил на ту же ось.

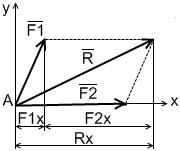
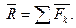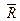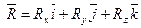Равнодействующая ССС находится по правилу параллелограмма: (*) Находим силу в декартовых координатах вторым способом: Находим проекции вектора, спроецировав векторное равенство на оси координат: .

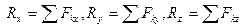Модуль равнодействующей и направляющие косинусы:

R = , .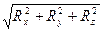

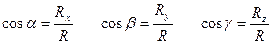Главный вектор и равнодействующая ССС

Главный вектор и равнодействующая ССС находятся по правилу параллелограмма: 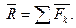, следовательно, эти два определения для ССС совпадают.

Необходимые и достаточные условия равновесия ССС

Формулируются в геометрической и аналитической форме.

1. Геометрическая форма. Для того, чтобы ССС находилась в равновесии необходимо и достаточно, чтобы главный вектор (равнодействующая) равнялся нулю

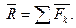= 0.

2.Аналитическая форма.

R = 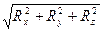= 0, если выполняются три условия:

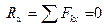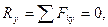1) , 2) 3)

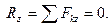
Для того, чтобы ССС находилась в равновесии необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую их трех координатных осей равнялись нулю.

Каждое из условий соответственно означает, что тело под действием ССС не совершает линейные перемещения вдоль координатных осей x,y,z.

Дата добавления: 2015-06-04