
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основная Теорема статики
|
|
|
|
ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЗАДАННОМУ ЦЕНТРУ.
Лекция 5
Для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций моментов пар сил на каждую из трех координатных осей была равна нулю.
Для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы момент эквивалентной пары сил равнялся нулю.
Необходимые и достаточные условия равновесия пар сил
1. Геометрическая форма
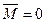
2. Аналитическая форма
M = 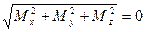 , если
, если 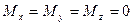 . Следовательно, аналитические условия равновесия имеют вид:
. Следовательно, аналитические условия равновесия имеют вид:
1) 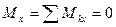 , 2)
, 2) 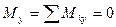 , 3)
, 3) 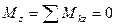 .
.
Лемма Пуансо
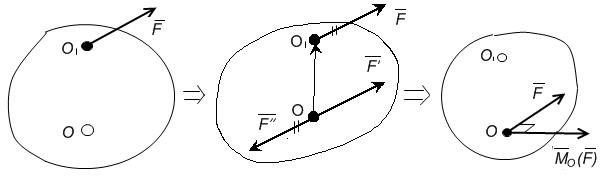
Равнодействующая системы сходящихся сил находится с помощью сложения сил по правилу параллелограмма. Очевидно, что аналогичную задачу можно будет решить и для произвольной системы сил, если найти для них метод, позволяющий перенести все силы в одну точку. Такой метод дает лемма Пуансо.
|
Сил а 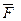 , приложенная в точке О1, эквивалентна геометрически равной ей силе , приложенная в точке О1, эквивалентна геометрически равной ей силе  в точке О и паре сил с моментом, равным моменту силы в точке О и паре сил с моментом, равным моменту силы 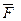 относительно точки О.
Пусть сила относительно точки О.
Пусть сила 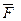 приложена в точке О1. Действие этой силы не изменяется, если в точке О приложить две уравновешенные силы, равные по модулю F. Полученная система трех сил представляет собой силу приложена в точке О1. Действие этой силы не изменяется, если в точке О приложить две уравновешенные силы, равные по модулю F. Полученная система трех сил представляет собой силу 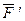 равную равную 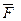 , но приложенную в точке О и пару , но приложенную в точке О и пару 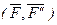 с моментом с моментом 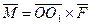 . .
|
Операция замены силы 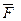 силой
силой 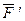 и парой сил
и парой сил 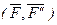 называется приведением силы
называется приведением силы 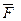 к заданному центру. Возникающая пара сил называется присоединенной.
к заданному центру. Возникающая пара сил называется присоединенной.
Основная теорема статики
Применяем теорему Пуансо к произвольной системе сил. Пусть точка О – центр приведения.
1) Выполняем параллельный перенос всех сил в точку О и получаем ССС. Находим геометрическую сумму всех сил - главный вектор СС.
Главным вектором системы сил называется вектор, равный векторной сумме этих сил.
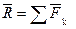 .
.
2) В точке О прикладываем вектор-моменты всех сил, равные моментам всех присоединенных ПС, и получаем вторую систему сходящихся векторов. Выполняем операцию геометрического сложения и находим главный момент СС относительно центра приведения.
Главным моментом системы сил относительно точки О тела, называется вектор, равный векторной сумме моментов всех сил системы относительно этой точки.
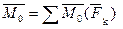
Основная теорема статики. Произвольная система сил при приведении к выбранному центру О эквивалентна одной силе, равной главному вектору системы сил, и одной паре сил с моментом, равным главному моменту системы сил относительно центра приведения.
Операция приведения к центру называется приведением СС к простейшему виду.
Определение главного вектора и главного момента системы сил
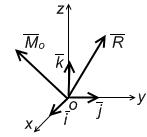
|
Главный вектор и главный момент определяются в декартовых координатах с помощью проекций:
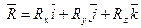 , , 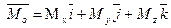 . .
|
Проекции векторов на оси координат:
 ,
, 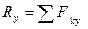 ,
, 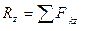
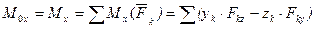 ,
,
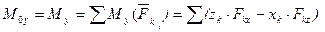 ,
,
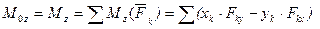 .
.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 434; Нарушение авторских прав?; Мы поможем в написании вашей работы!