
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 0
|
|
|
|
Вопросы и задачи для самоконтроля
1. Как записывается условие равенства нулю главного вектора сил, действующих на плавающее тело?
2. Удовлетворение какого условия обуславливает равенство нулю главного момента сил, действующих на плавающее тело?
3. Что понимают под устойчивостью положения равновесия плавающего тела?
4. Поперечный метацентр судна есть центр кривизны некоторой кривой. Какие точки образуют эту кривую?
5. Может ли плавать не опрокидываясь судно, если его центр тяжести G расположен выше центра поддержания C?
6. Найдите угол крена 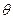 , для которого формула (11.5) верна с точностью 5%?
, для которого формула (11.5) верна с точностью 5%?
7. Почему надводные корабли могут иметь крен на циркуляции как в сторону ее центра, так и в противоположную?
СПИСОК ЛИТЕРАТУРЫ
1. Н.В. Бутенин, Я.Л. Лунц, Д.Р.Меркин., Курс теоретической механики, Т.1, Наука, Москва, 1971г.
2. И.В. Мещерский., Задачи по теоретической механике, Москва, 2002 г.
Элементы векторной алгебры
В теоретической механике рассматриваются такие векторные величины как сила, моменты силы относительно точки и оси, момент пары сил, скорость, ускорение и другие.
1. Понятие вектора.
Для определенности рассматриваем прямоугольную декартову систему координат.
Вектор это направленный отрезок, который характеризуется длиной и направлением.
Операции над векторами. Векторы можно складывать и умножать на число.
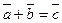 сумма двух векторов есть вектор
сумма двух векторов есть вектор
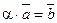 произведение вектора на действительное число есть вектор
произведение вектора на действительное число есть вектор
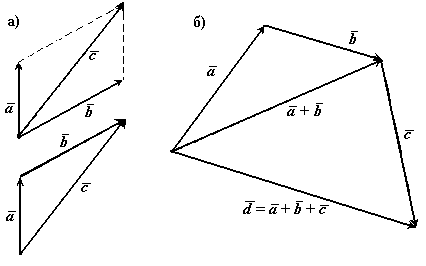 |
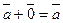 существует нулевой вектор
существует нулевой вектор
В математике все векторы являются свободными, их можно переносить параллельно самим себе.
В сумме двух векторов начало второго вектора можно поместить в конец первого вектора, тогда сумму двух векторов можно представить как вектор, имеющий начало в начале первого вектора, а конец в конце второго вектора. Применяя это правило для суммы нескольких векторов получаем, что суммой нескольких векторов является вектор, замыкающий ломаную линию, состоящую из слагаемых векторов.
Операции над векторами подчиняются следующим законам:
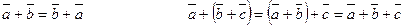

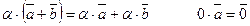
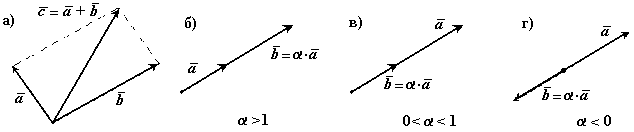
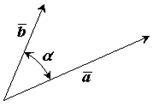
2. Скалярное произведение двух векторов
Имеется два вектора 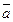 и
и 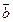 .
. 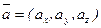 ,
, 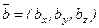 .
.
 Результатом скалярного произведения двух векторов
Результатом скалярного произведения двух векторов 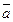 и
и 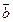 является скалярная величина (число).
является скалярная величина (число).
Записывается как 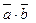 или
или 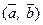 . Скалярное произведение двух векторов равно
. Скалярное произведение двух векторов равно 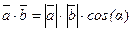
Свойства скалярного произведения:

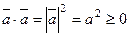

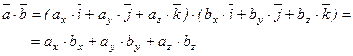
3. Векторное произведение двух векторов
Имеется два вектора 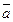 и
и 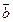 .
. 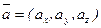 ,
, 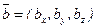 .
.
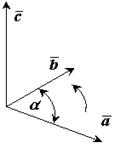 Результатом векторного произведения двух векторов
Результатом векторного произведения двух векторов 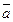 и
и 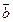 является вектор
является вектор 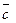 . Записывается как
. Записывается как 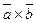 или
или 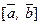 . Векторное произведение двух векторов это вектор
. Векторное произведение двух векторов это вектор 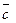 , перпендикулярный к обоим этим векторам, и направленный так, чтобы с его конца поворот вектора
, перпендикулярный к обоим этим векторам, и направленный так, чтобы с его конца поворот вектора 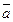 к вектору
к вектору 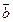 был виден против хода часовой стрелки.
был виден против хода часовой стрелки.
Длина (или модуль) векторного произведения равна 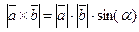 .
.
Свойства векторного произведения:
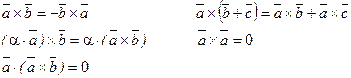
Векторное произведение двух векторов вычисляется через их проекции следующим образом:
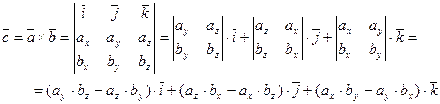
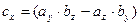
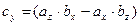
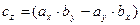
4. Длина, проекции и направляющие косинусы вектора
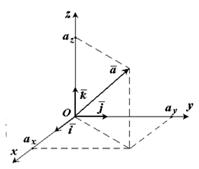
Единичные вектора вдоль осей Ox, Oy и Oz образуют систему единичных (или базисных) векторов. Любой вектор, имеющий начало в точке O, можно представить как сумму 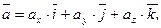 числа (ax, ay, az) - это проекции вектора
числа (ax, ay, az) - это проекции вектора 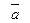 на оси координат.
на оси координат.
Длина (или модуль) вектора 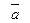 определяется формулой
определяется формулой 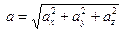 и обозначается
и обозначается 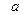 или
или 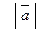 .
.
Проекцией вектора на ось называется скалярная величина, равная произведению модуля вектора на косинус угла, образованного с положительным направлением координатной оси. Проекция вектора считается положительной (+), если направление ее совпадает с положительным направлением оси, и отрицательной (-), если проекция направлена в противоположную сторону.
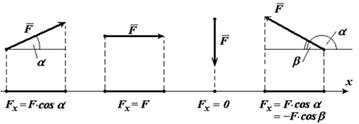 Направляющими косинусами cos a, cos b, cos g вектора называются косинусы углов между вектором и положительными направлениями осей Ox, Oy и Oz соответственно.
Направляющими косинусами cos a, cos b, cos g вектора называются косинусы углов между вектором и положительными направлениями осей Ox, Oy и Oz соответственно.
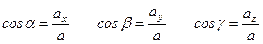
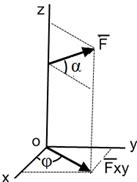
| Проекция вектора на плоскость – есть вектор, заключенный между проекцией начала и конца вектора на эту плоскость. Модуль вектора: Fxy = Fcosα. Для определения проекций вектора на оси координат используется метод двойного проецирования: Fx = Fxy cosφ = F cosα cosφ, Fy = Fxy sinφ = Fcosα sinφ, Fz = F sinα. |
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 540; Нарушение авторских прав?; Мы поможем в написании вашей работы!