Вывод формулы начальной остойчивости

Вычислим теперь величину восстанавливающего момента, действующего на наклоненное плавающее тело. Из рисунка 11.2 видно, что плечо пары сил веса и поддержания может быть вычислено как ,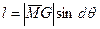

а возникающий при этом бесконечно малый восстанавливающий момент как

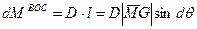(11.4)

Введем обозначения:

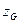- аппликата центра тяжести тела в положении равновесия, 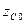- аппликата центра величины погруженного объема.

Тогда 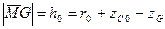– возвышение центра кривизны М над центром тяжести тела G.

Формула (11.4) выведена для бесконечно малого наклонения, но ее можно использовать и для небольших конечных углов (т.е. 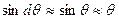). Тогда формулу можно переписать в виде

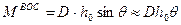(11.5)

Примечания:

1. Формула (11.5) справедлива для любых плавающих тел, в том числе и для водоизмещающих судов любых типов. Начальной остойчивостью судна называется способность находящегося в равновесии судна сопротивляться любому воздействию, вызываемому внешними или внутренними причинами, стремящемуся вывести его из исходного положения равновесия при малых начальных отклонениях. Если наклон происходит только в поперечной плоскости судна, то угол наклона будет называться углом крена, а формула (11.5) носит название метацентрической формулы поперечной остойчивости. Величина 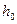, входящая в (11.5), при наклоне судна только в поперечной плоскости судна, называется поперечной или малой метацентрической высотой, величина 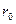- малым метацентрическим радиусом, точка М – поперечным метацентром судна. Если наклон происходит в диаметральной плоскости судна, то угол наклона называется углом дифферента, а метацентрическая высота называется продольной или большой.

2. При рассмотрении тела, полностью погруженного в жидкость (подводные аппараты, подводные лодки и т.п.), условия равновесия остаются прежними: вес тела и сила поддержания должны быть равны, а центры приложения этих сил должны располагаться на одной вертикали. Отличие этого случая от рассмотренного ранее состоит в неизменности при наклонении тела положения его центра величины (центр величины и метацентр совпадают). Очевидно, что положение равновесия полностью погруженного тела устойчиво, если центр величины располагается выше центра тяжести (это возвышение оказывается метацентрической высотой для наклонения тела в любой плоскости). Величина восстанавливающего момента, препятствующего наклонению полностью погруженного тела, рассчитывается, как и прежде, по формуле (11.5).

Пример 11.1: На прямоугольном понтоне длины L, ширины B и осадки T в диаметральной плоскости имеется груз веса P. Зная аппликату центра тяжести понтона с грузом 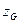, найти выражение для угла крена понтона при смещении груза к борту на расстояние 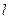. До перемещения груза углы крена и дифферента понтона равнялись нулю.

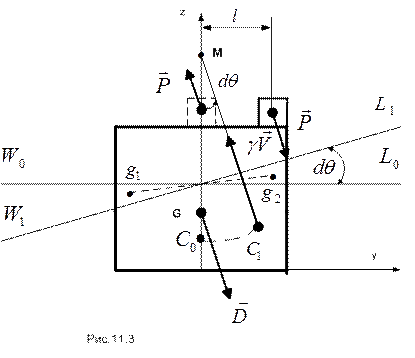
Перемещение груза (снятие его из начального положения и перенос в новое) вызывает возникновение пары сил, стремящихся наклонить понтон. Полагая возникающий угол крена небольшим (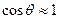), кренящий момент этой пары сил равен

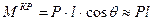
Момент пары сил, стремящийся вернуть понтон в исходное положение, рассчитывается по формуле (11.5) как

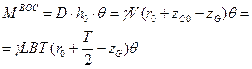
где 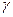- удельный вес воды, V – объем подводной части понтона.

В формуле учтено, что объем подводной части понтона равен произведению его длины, ширины и осадки, а аппликата центра величины погруженного объема равна половине осадки.

Схема сил, действующих на понтон в этой ситуации, изображена на рис. 11.3.

Приравняв кренящий и восстанавливающий моменты, получим уравнение для угла крена понтона:

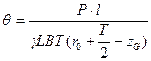
Вычислим малый метацентрический радиус 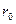. Для этого дадим понтону небольшое (край борта не погружается в воду, край днища не выходит из воды) равнообъемное наклонение на угол 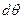. Ось поворота делит пополам прямоугольник ватерлинии. В этом случае объемы входящего и выходящего клиньев одинаковы и равны

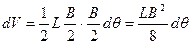
Расстояние между центрами тяжести клиньев будет .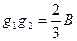

Подставив полученные значения в формулу для длины дуги, имеем

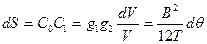
Теперь вычислим малый (поперечный) метацентрический радиус прямоугольного понтона как

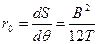
Окончательное выражение для угла крена принимает вид

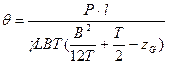
Пример 11.2: Прямоугольный понтон длины L и ширины B, плавая без крена и дифферента, имеет осадку Т, высоту надводного борта H < T и аппликату центра тяжести .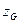

Осуществим буксировку понтона, приложив силу к точке палубы, расположенной в верхнем углу сечения понтона диаметральной плоскостью. Силу сопротивления воды, возникающую при буксировке понтона с постоянной скоростью, будем полагать равной

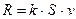
где 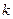- эмпирический коэффициент, S – площадь наибольшего погруженного поперечного сечения, 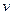- скорость буксировки; точка приложения силы сопротивления находится в центре площади S. Найти величину скорости буксировки, при которой начинается заливание палубы понтона. Процесс образования волн не учитывать.

Изобразим понтон в предельном положении, когда край палубы находится на уровне воды (см. рис. 11.4).

Полагая угол дифферента понтона небольшим, запишем выражение для его определения как

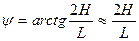
Нанесем на рисунок силы, действующие на понтон (сила тяги F, сила сопротивления R, сила веса D и сила поддержания 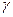V). Заметим, что крен понтона равен нулю, так как все силы расположены в его диаметральной плоскости. Постоянство скорости буксировки позволяет рассмотреть равновесие системы сил, приложенных к понтону.

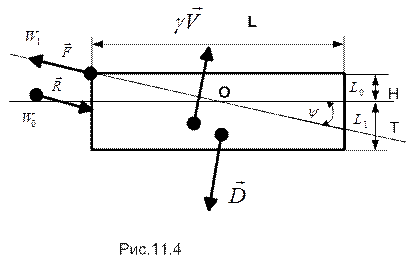
Приравнивая нулю проекцию на ватерлинию главного вектора сил, получаем, что величины сил тяги и сопротивления должны быть равными. В таком случае пара этих сил создает момент, стремящийся наклонить понтон. При небольшом угле дифферента (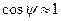) этот момент равен

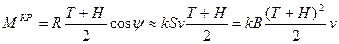
При выводе формулы полагалось, что при сделанном допущении площадь наибольшего погруженного поперечного сечения равна

.

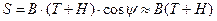Пара сил веса и поддержания создает восстанавливающий момент, равный, согласно формуле (11.5)

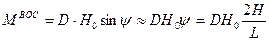
Здесь 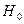- большая (или продольная) метацентрическая высота понтона. Ее величина рассчитывается по формуле, структура которой аналогична выведенной выше для малой метацентрической высоты, т.е.

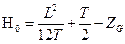
Приравняв кренящий и восстанавливающий моменты, получим выражение для интересующей нас скорости буксировки

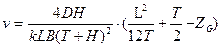
Пример 11.3: Подводная лодка (ПЛ), двигаясь в подводном положении в горизонтальной плоскости с постоянной по величине скоростью 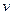, совершает циркуляцию радиуса 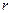(см. рис. 11.5).

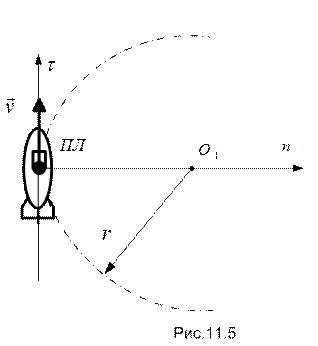
Найти выражение для угла крена ПЛ, возникающего при выполнении этого маневра, если известны ее водоизмещение D, поперечная метацентрическая высота h=CG и расстояние от точки приложения силы бокового давления до центра тяжести OG=d.

Указание: при рассмотрении равновесия ПЛ в поперечной плоскости в ее центре тяжести следует дополнительно приложить силу инерции, направленную вдоль радиуса циркуляции и вычисляемую как

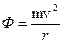, где m –масса ПЛ с учетом присоединенной массы воды в поперечном направлении (ее величину полагать известной).

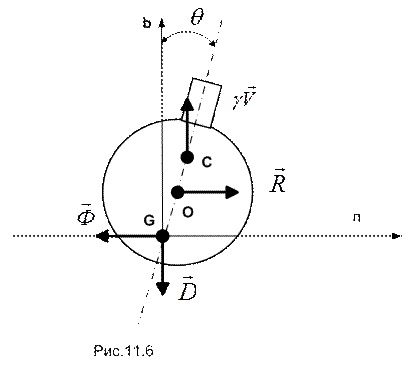
Изобразим на рис. 11.6 плоскость, нормальную к траектории движения ПЛ (плоскость, проходящую через главную нормаль и бинормаль к траектории), ПЛ и силы, на нее действующие.

Поскольку при выполнении заданного маневра угол крена не изменяется, для изображенной системы сил можно записать систему уравнений равновесия:

.

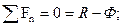
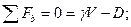
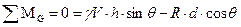Решив систему относительно угла крена 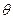, получим

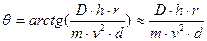
Замечания:

1. В силу конструктивных особенностей центр тяжести ПЛ располагается ниже точки приложения силы бокового давления, поэтому при циркуляции ПЛ наклоняется в сторону центра кривизны траектории движения.
2. У надводных судов расположение центра тяжести может быть как ниже, так и выше точки приложения силы бокового давления. Очевидно, что в последнем случае судно будет наклонено в противоположную от центра кривизны сторону.

Дата добавления: 2015-06-04