Статика плавающего тела

Вопросы и задачи для самоконтроля

1. Какие тела называются частично закрепленными?

2. В каком случае уравнения равновесия могут не содержать опорных реакций?

3. Какое положение равновесия называется устойчивым (неустойчивым, безразличным)?

4. Что понимают под терминами опрокидывающий и восстанавливающий моменты?

5. Обратный математический маятник длиной 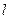и веса 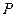прикреплен к земле спиральной пружиной жесткости 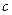. Определить, при каком соотношении заданных величин вертикальное положение обратного маятника оказывается устойчивым. Определить угол отклонения математического маятника для случая, когда полученное соотношение не выполняется. Будет ли это положение равновесия устойчивым?

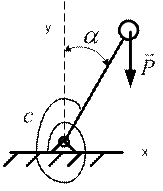
11.1.Условия равновесия плавающего тела. Анализ устойчивости положения равновесия

Весом (или в одоизмещением) плавающего тела называется равнодействующая параллельных сил весов его элементов. Равнодействующая сил, приложенных со стороны жидкости к корпусу судна (сила Архимеда) называется силой поддержания. Точки приложения этих сил называются, соответственно, центром тяжести G и центром величины C погруженного объема тела.

Для плавающего тела первое условие равновесия (равенство нулю главного вектора сил) можно записать в виде

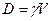(11.1)

где – вес тела, 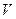– погруженный объем тела, 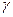- удельный вес жидкости.

Второе условие равновесия (равенство нулю главного момента сил) имеет место только в том случае, если точки G и C находятся на одной вертикали.

Рассмотрим сначала тело, поверхность которого пересекает поверхность жидкости (надводные корабли и суда, плавучие буровые платформы и т.п.).

При равнообъемном наклонении тела (для выполнения первого условия равновесия объем погруженной части при наклоне не должен изменяться) точка С перемещается в сторону наклона; положение точки G по отношению к телу, естественно, не меняется.

Если после наклона точки G и C располагаются не на одной вертикали, то вес тела D и сила поддержания 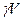образуют пару сил с моментом 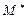. Момент пары, увеличивающий угол наклона, будем считать положительным. Очевидно, что при отрицательном моменте пары первоначальное положение тела будет устойчиво (на рис. 11.1.а,б момент пары оказывается восстанавливающим), в случае положительного момента (рис. 11.1.г) первоначальное положение равновесия тела неустойчиво, а при 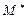= 0 положение равновесия безразличное.

На рис. 11.1 точкам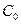и и 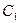обозначены центры погруженного объема тела в его не наклоненном и наклоненном положениях, точкой М – центр кривизны дуги .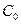

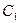Таким образом, под устойчивостью положения равновесия плавающего тела понимается свойство возвращаться в него после освобождения от причин, вызвавших этот наклон. Анализ рисунка показывает, что если в положении равновесия точка М располагается над точкой G, то при наклоне момент пары сил оказывается восстанавливающим; при расположении точки G выше точки М – момент оказывается опрокидывающим, а при совпадении этих точек положение равновесия будет безразличным (просматривается механическая аналогия с задачей 10.3).

Выше достаточно подробно обсуждался вопрос о способах нахождения центра параллельных сил, поэтому на определении положения точек G, 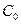и 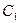останавливаться не будем.

Обсудим расчет положения точки М.

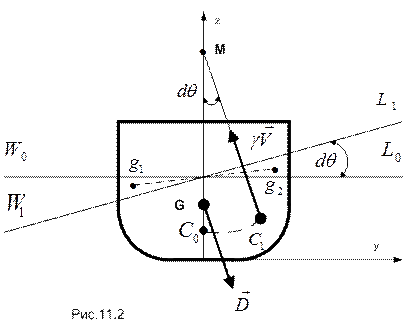
При бесконечно малом равнообъемном наклонении тела на угол 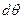ватерлиния WL поворачивается из положения 0 в положение 1 (см. рис. 11.2).

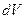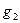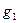При этом в жидкость с одной стороны дополнительно входит объем тела , а с другой такой же объем выходит. Центры тяжести входящего и выходящего объемов обозначены на рисунке и , соответственно. Направление перемещения центра тяжести объема 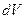совпадает с линией 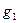- 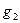, а величина перемещения равна длине отрезка .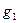

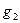Обозначив через 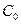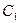перемещение центра тяжести погруженного объема тела в целом, можно написать:

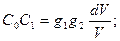(11.2)

(отрезк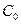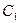и и 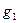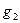параллельны).

Радиус кривизны дуги 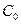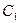будет 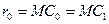. Из курса математики известно, что величина радиуса кривизны кривой есть частное от деления бесконечно малой длины дуги на бесконечно малый угол поворота этого радиуса. Делая допущение о равенстве длин дуги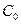 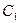и соответствующей хорды, можно определить величину радиуса кривизны 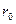как

(11.3)

Дата добавления: 2015-06-04