Условия равновесия частично закрепленного тела

РАВНОВЕСИЕ ЧАСТИЧНО ЗАКРЕПЛЕННОГО ТЕЛА. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ ПОЛОЖЕНИЯ РАВНОВЕСИЯ

Вопросы и задачи для самоконтроля

1. Какова размерность коэффициента трения скольжения?

2. Какова размерность коэффициента трения качения?

3. Можно ли использовать формулу (9.1), если сила трения не достигла предельного значения? Как в этом случае определить величину силы трения?

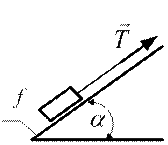
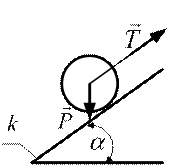
4. Определить минимальную ситу натяжения нити, необходимую для начала движения вверх бруска веса Р по наклонной шероховатой плоскости.

5. Выберете вариант вычисления силы 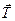, необходимой для начала качения колеса без проскальзывания вверх по наклонной плоскости. Вес колеса Р, его радиус 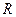, угол наклона 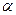и коэффициент трения качения 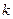известны.

В некоторых случаях приходится рассматривать равновесие частично закрепленных тел, т.е. тел, на которые наложены связи, допускающие перемещение тела. В качестве примеров, на рис. 10.1.а,б,в, изображены тела, имеющие ось вращения, шарнирно неподвижную опору и опору в виде стержня с шарнирами на концах.

Если для любого из тел отбросить наложенные связи и заменить их соответствующими реакциями, то для полученных силовых схем можно записать уравнения равновесия. В общем случае неизвестными величинами оказываются не только реакции связей, но и параметры положения равновесия (линейные, угловые). Однако, при соответствующем выборе координатной системы, некоторые уравнения могут не содержать опорных реакций. Так, например, для тела, изображенного на рис. 10.1.а, сумма моментов сил относительно оси АВ не будет включать опорных реакций (силы реакций ось пересекают). Не будет опорных реакций и в уравнениях моментов относительно неподвижного шарнира О для тела, изображенного на рис.10.1.б, а так же в уравнениях моментов относительно подвижного шарнира В для тела, изображенного на рис. 10.1.в.

На практике встречаются две постановки задачи. В первой требуется найти параметры положений равновесия (в общем случае положений равновесия может быть несколько) и (или) величины возникающих при этом опорных реакций, а так же проанализировать устойчивость найденных положений равновесия. Во второй – найти опорные реакции и соотношения между активными силами, действующими на тело в заданном положении равновесия.

Получение схемы сил, действующих на тело, а так же составление системы уравнений равновесия является необходимым при решении задачи в любой постановке.

Поясним сказанное на примерах:

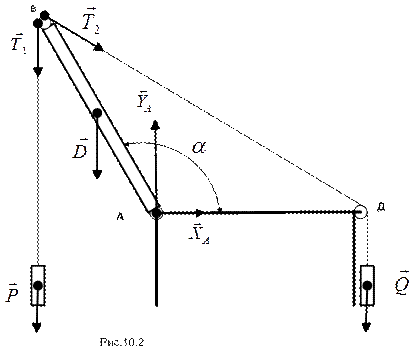
Пример 10.1. (задача 4.1 из [ 2 ]). На рис. 10.2 изображен однородный стержень АВ, прикрепленный к горизонтальному основанию шарниром в точке A.

К концу B прикреплены две невесомые нити; на одной подвешен груз Р = 10 кН, на другой, переброшенной через блок в точке Д, груз Q = 20 кН. Вес стержня D = 20 кН, АВ = AД. При каком угле с основанием стержень будет находиться в равновесии?

Освободим стержень АВ от связей (шарнир A и нити) и приложим в точках контакта связей соответствующие реакции (при этом величины сил натяжения нитей равны, соответственно, 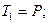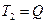). Для исключения из рассмотрения неизвестных составляющих в шарнире A, запишем сумму моментов сил относительно этой точки:

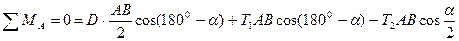
Подставив числовые значения и решив уравнение, получим: .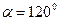

Если бы в задаче требовалось найти величины составляющих реакции в шарнире A, их следовало бы найти из соответствующих уравнений равновесия: равенств нулю сумм проекций сил на горизонтальную и вертикальную оси.

Устойчивость найденного положения равновесия будет проанализирована ниже.

Пример 10.2. На горизонтальной поверхности стоит кран. Вес крана Q, расстояние между опорами H, вылет стрелы L, вес груза P. Центр тяжести крана делит расстояние между опорами пополам (см. рис. 10.3). Найти максимальную величину груза, поднимаемого краном.

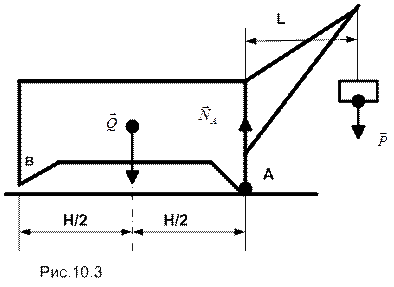
В рабочем положении кран опирается на горизонтальную поверхность двумя точками (задачу полагаем плоской). Очевидно, что максимальный вес груза, стремящийся вывести кран из положения равновесия (т.е. опрокинуть его), приводит к отрыву от поверхности опоры В крана и, как следствие, отсутствию в этой точке силы реакции опоры.

Выбрав за центр приведения точку А, составим уравнение равновесия моментов сил, действующих на кран:

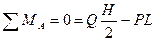
Из уравнения находим величину максимального веса груза: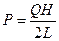

Примечание: существует трактовка, при которой моменты сил, действующих на тело, подразделяются на опрокидывающие (стремящиеся отклонить тело от положения равновесия) и восстанавливающие (стремящиеся вернуть тело в исходное положение). Тогда уравнение равновесия для моментов сил может быть записано как равенство опрокидывающего и восстанавливающего моментов. Соотношение между этими моментами в отклоненном от равновесного положении есть ключ к анализу его устойчивости.

Например, для крана момент силы веса груза Р является опрокидывающим, а момент веса крана Q – восстанавливающим.

Анализ устойчивости рабочего положения крана будет выполнен ниже.

Дата добавления: 2015-06-04